© ГДЗ 8next.com, 2013, 2018, 2022
Питання
1. Які властивості має об'єм фігури? Рівні фігури мають рівні об’єми. Об’єм фігури дорівнює сумі об’ємів фігур, з яких вона складається.
2. Наведіть приклади одиниць виміру об'єму. Кубічний міліметр (мм3), кубічний сантиметр (см3), кубічний дециметр (дм3), літр (л), кубічний метр (м3), кубічний кілометр (км3).
3. Що означає виміряти об'єм фігури? Виміряти об’єм фігури — це означає підрахувати, скільки одиничних кубів у ній вміщується.
4. Чому дорівнює об'єм прямокутного паралелепіпеда з вимірами а, Ь і с. Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів.
5. За якою формулою обчислюють об'єм куба? V = аЬс, де V — об’єм паралелепіпеда, а, Ь і с — його виміри, виражені в одних і тих самих одиницях.
6. Як обчислити об'єм прямокутного паралелепіпеда, якщо відомо його площу основи та висоту? Об'єм прямокутного паралелепіпеда дорівнює добутку площі основи на висоту V = S•h
Розв’язуємо усно
Завдання 1. Ділянку дороги завдовжки 3 км, на якій швидкість автомобіля не має перевищувати 60 км/год, водій проїхав за 3 хв. Чи порушив при цьому водій правила дорожнього руху?
Розв’язання
3 км = 3000 м
3000 м : 3 хв = 1 000 м/хв = 1 км/хв– швидкість руху автомобіля.
1 км/хв = 60 км/год
Відповідь: не порушив.
Завдання 2 Скільки потрібно використати кубиків з ребром 1 см, щоб скласти кубик з ребром 2 см?
Розв’язання
Куб з вимірами 2 см • 2 см • 2 см буде містити 2 • 2 • 2 = 8 одиничних кубів.
Завдання 3 Скільки сантиметрів дроту необхідно для виготовлення дротяного каркаса прямокутного паралелепіпеда, виміри якого дорівнюють 3 см, 5 см і 6 см?
Розв’язання
3 см • 4 + 5 см • 4 + 6 см • 4 = 56 (см) – довжина дротяного каркаса.
Завдання 4 (Задача-жарт) У двох гаманцях лежать дві монети, причому в одному гаманці монет удвічі більше, ніж у другому. Чи можливе таке? Можливо, коли один гаманець міститься всередині іншого.
Вправи
Вправа 660°
1) Скільки кубічних сантиметрів міститься в 1 дм3? в 1 м3?
1 дм3 = 1 дм • 1 дм • 1 дм = 10 см • 10 см • 10 см = 1 000 см3
1 м3 = 1 м • 1 м • 1 м = 100 см • 100 см • 100 см = 1 000 000 см3
2) Скільки кубічних дециметрів міститься в 1 м3?
1 м3 = 1 м • 1 м • 1 м = 10 дм • 10 дм • 10 дм = 1 000 дм3
Вправа 661°Які одиниці об’єму доцільно використовувати для вимірювання об’єму:
1) класної кімнати; м3
2) рідини, яку має вживати людина протягом доби; л
3) коробки сірників? мм3
Вправа 662° Фігури, зображені на рисунку 188, складено з кубиків, ребра яких дорівнюють 1 см. Знайдіть об’єм кожної фігури.
Розв’язання
1 см • 1 см • 1 см = 1 см3 – об'єм одного кубика.
а) 1 см3 • 4 = 4 см3 – об'єм першої фігури.
б) 1 см3 • 6 = 6 см3 – об'єм другої фігури.
в) 1 см3 • 12 = 12 см3 – об'єм третьої фігури.
г) 1 см3 • 10 = 10 см3 – об'єм четвертої фігури.
Вправа 663° Фігури, зображені на рисунку 189, складено з кубиків, ребра яких дорівнюють 1 см. Знайдіть об’єм кожної фігури.
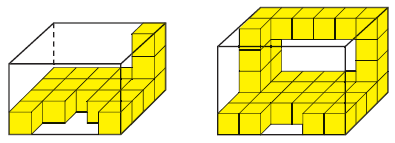
Розв’язання
Об’єм дорівнює кількості об’ємів кубиків.
1) 1 см3 • 18 = 18 см3 – об’єм першої фігури.
2) 1 см3 • 35 = 35 см3 – об’єм другої фігури.
Вправа 664° Обчисліть об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 12 м, 15 м і 6 м .
Розв’язання
V = 12 м • 15 м • 6 м = 1080 м3 – об’єм прямокутного паралелепіпеда.
Відповідь: об’єм прямокутного паралелепіпеда дорівнює 1080 м3.
Вправа 665° Знайдіть об’єм куба, ребро якого дорівнює 6 см.
V = 63 см3 = 216 см3 – об’єм куба з ребром 6 см.
Відповідь: об’єм куба з ребром 6 см дорівнює 216 см3.
Вправа 666° Чому дорівнює об’єм прямокутного паралелепіпеда з вимірами 10 дм, 8 дм і 4 дм?
Розв’язання
V = 10 дм • 8 дм • 4 дм = 320 дм3 – об’єм прямокутного паралелепіпеда.
Відповідь: об’єм прямокутного паралелепіпеда 320 дм3.
Вправа 667° Ящик з якими вимірами є більш містким — із вимірами 15 см, 20 см і 30 см чи з вимірами 45 см, 10 см, 18 см?
Розв’язання
1) V1 = 15 см • 20 см • 30 см = 9 000 см3 – об’єм ящика з вимірами 15 см, 20 см і 30 см.
2) V2 = 45 см • 10 см • 18 см = 8 100 см3 – об’єм ящика з вимірами 45 см, 10 см і 18 см.
9 000 см3 > 8 100 см3
Відповідь: більший ящик з вимірами 15 см, 20 см і 30 см.
Вправа 668° (Домашня практична робота) Знайдіть вдома предмет, який має форму прямокутного паралелепіпеда. Виконайте потрібні вимірювання та обчисліть його об’єм. Шафа-пенал із вимірами 6 дм, 5 дм і 20 дм
Розв’язання
V = 6 дм • 5 дм • 20 дм = 600 дм3– об’єм шафи-пенала з вимірами 6 дм, 5 дм і 20 дм.
Відповідь: 600 дм3.
Вправа 669° Обчисліть об’єм прямокутного паралелепіпеда, якщо S = 15 см2 , h = 6 см, де S — площа основи паралелепіпеда, h — його висота.
Розв’язання
V = Sh = 15 cм2 • 6 cм = 90 cм3– об’єм прямокутного паралелепіпеда.
Відповідь: 90 см3.
Вправа 670 Виразіть:
1) у кубічних міліметрах: 7 см3; 12 см3 243 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3;
7 см3 = 7 • 10 мм • 10 мм • 10 мм = 7000 мм3
12 см3 243 мм3 = 12 • 10 мм • 10 мм • 10 мм + 243 мм3 = 12000 мм3 + 243 мм3 =
= 12 243 мм3
54 см3 4 мм3 = 54 000 мм3 + 4 мм3 = 54 004 мм3
1 дм3 20 мм3 = 1 000 000 мм3 + 20 мм3 = 1 000 020 мм3
18 дм3 172 см3 = 18 000 000 мм3 + 172 000 мм3 = 18 172 000 мм3
2) у кубічних дециметрах: 4 м3; 28 м3 2 дм3; 5 430 000 см3.
4 м3 = 4 • 10 дм • 10 дм • 10 дм = 4000 дм3
28 м3 2 дм3 = 28 • 10 дм • 10 дм • 10 дм + 2 дм3 = 28 000 дм3 + 2 дм3 = 28 002 дм3
5 430 000 см3 = 5430 • 1 дм • 1 дм • 1 дм = 5430 дм3
Вправа 671 Виразіть у кубічних сантиметрах: 62 дм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3.
62 дм3 = 62 • 10 см • 10 см • 10 см = 62 000 см3
520 000 мм3 = 520 • 1 см • 1 см • 1 см = 520 см3
78 дм3 325 см3 = 78 000 см3 + 325 см3 = 78 325 см3
56 дм3 14 см3 = 56 000 см3 + 14 см3 = 56 014 см3
Вправа 672 Ширина прямокутного паралелепіпеда дорівнює 15 дм, довжина на 3 дм більша за ширину, а висота у 3 рази менша від довжини. Знайдіть об’єм даного паралелепіпеда.
Розв’язання
1) 15 + 3 = 18 (дм) – довжина прямокутного паралелепіпеда.
2) 18 : 3 = 6 (дм) – висота прямокутного паралелепіпеда.
3) V = 18 дм • 15 дм • 6 дм = 1620 дм3 – об’єм даного паралелепіпеда.
Відповідь: об’єм даного паралелепіпеда 1620 дм3.
Вправа 673 Висота прямокутного паралелепіпеда дорівнює 20 см, що на 4 см менше від його довжини і в 5 разів більше за його ширину. Обчисліть об’єм даного паралелепіпеда.
Розв’язання
1) 20 + 4 = 24 (см) – довжина прямокутного паралелепіпеда.
2) 20 : 5 = 4 (см) – ширина прямокутного паралелепіпеда.
3) V = 24 см • 4 см • 20 см = 1920 см3– об’єм прямокутного паралелепіпеда.
Відповідь: об’єм прямокутного паралелепіпеда 1920 см3.
Вправа 674 Об’єм прямокутного паралелепіпеда дорівнює 560 см3, довжина — 14 см, ширина — 8 см. Знайдіть висоту даного паралелепіпеда.
Короткий запис
а = 14 см
b = 8 см
V = 560 см3
h – ?
Розв’язання
1) S = а • b = 14 см • 8 см = 112 см2 – площа основи паралелепіпеда.
2) h = V : S = 560 см3 : 112 см2 = 5 см – висота даного паралелепіпеда.
Відповідь: висота даного паралелепіпеда 5 см.
Вправа 675 Довжина прямокутного паралелепіпеда дорівнює 18 см, висота — 15 см, а об’єм — 3240 см3. Знайдіть ширину даного паралелепіпеда.
Короткий запис
а = 18 см
h = 15 см
V = 3240 см3
b – ?
Розв’язання
b = V : а : h = 3240 см3 : 18 см : 15 см = 12 см – ширина даного паралелепіпеда.
Відповідь: ширина даного паралелепіпеда 12 см.
Вправа 676 Об’єм кімнати, яка має форму прямокутного паралелепіпеда, дорівнює 144 м3, а висота — 4 м. Знайдіть площу підлоги кімнати.
Короткий запис
V = 144 м3
h = 4 м
S – ?
Розв’язання
S = V : h = 144 м3 : 4 м = 36 м2 – площа підлоги кімнати.
Відповідь: площа підлоги кімнати 36 м2.
Вправа 677 Площа підлоги спортивного залу, який має форму прямокутного паралелепіпеда, дорівнює 192 м2, а його об’єм — 960 м3. Знайдіть висоту спортивного залу.
Короткий запис
S = 192 м2
V = 960 м3
h – ?
Розв’язання
h = V : S = 960 м3 : 192 м2 = 5 м – висота спортивного залу.
Відповідь: висота спортивного залу 5м.
Вправа 678 Знайдіть об’єм фігури, зображеної на рисунку 190 (розміри дано в сантиметрах).
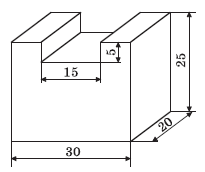
Розв’язання
Загальний об’єм знайдемо через різницю таких об’ємів.
1) V1 = 30 см • 20 см • 25 см = 15000 см3
2) V2 = 15 см • 20 см • 5 см = 1500 см3
3) V = V1 – V2 = 15000 см3 – 1500 см3 = 13500 см3.
Відповідь: об’єм фігури 13500 см3.
Вправа 679 Знайдіть об’єм фігури, зображеної на рисунку 191 (розміри дано в сантиметрах).
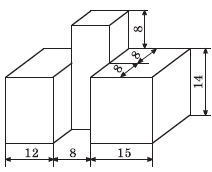
Розв’язання
Загальний об’єм знайдемо через суму таких об’ємів.
1) V1 = 12 см • (8 см + 8 см) • 14 см = 2688 см3
2) V2 = 8 см • 8 см • (14 см + 8 см) = 1408 см3
3) V3 = 15 см • (8 см + 8 см) • 14 см = 3360 см3
4) V = V1 + V2 + V3 = 2688 см3 + 1408 см3 + 3360 см3 = 7456 см3.
Відповідь: об’єм фігури 7456 см3.
Вправа 680 Ребро куба, виготовленого з цинку, дорівнює 4 см. Знайдіть масу куба, якщо маса 1 см3 цинку становить 7 г.
Розв’язання
1) 43 = 64 (см3) – об’єм куба.
2) 7 • 64 = 448 (г) – маса куба.
Відповідь: маса куба 448 г.
Вправа 682 Резервуар для води має форму прямокутного паралелепіпеда, виміри якого дорівнюють 6 м, 4 м і 5 м. Скільки тонн води вміщує цей резервуар, якщо маса 1 л води становить 1 кг?
Розв’язання
V = 6 • 4 • 5 = 120 (м3) – об’єм резервуару.
Для води: 120 м3 = 120 000 дм3 = 120 000 л = 120 000 кг = 120 т.
Відповідь: 120 тонн.
Вправа 683 Скільки літрів води можна налити в резервуар, який має форму прямокутного паралелепіпеда з вимірами 1 м 40 см, 50 см і 1 м 20 см?
Розв’язання
1 м 40 см = 14 дм, 50 см = 5 дм, 1 м 20 см = 12 дм
V = 14 • 5 • 12 = 840 (дм3) – об’єм резервуару.
Для води: 840 дм3 = 840 л
Відповідь: 840 літрів.
Вправа 684 Куб і прямокутний паралелепіпед мають рівні об’єми. Знайдіть площу поверхні куба, якщо довжина прямокутного паралелепіпеда дорівнює 12 см, що у 2 рази більше за ширину і в 4 рази більше за висоту паралелепіпеда.
Розв’язання
1) 12 : 2 = 6 (см) – ширина паралелепіпеда.
2) 12 : 4 = 3 (см) – висота паралелепіпеда.
3) V = 12 см • 6 см • 3 см = 216 см3 – об’єм паралелепіпеда або куба.
Об'єми рівні, тому V = 216 см3 = 6 см • 6 см • 6 см
4) оскільки ребро куба дорівнює 6 см, маємо
6 • 6 = 36 (см2) – площа грані куба.
5) оскільки куб має 6 граней, маємо
36 • 6 = 216 см2 – площа поверхні куба.
Відповідь: площа поверхні куба 216 см2.
Вправа 685 Прямокутний паралелепіпед і куб мають рівні об’єми. Знайдіть площу поверхні паралелепіпеда, якщо два його виміри дорівнюють 8 см і 25 см, а ребро куба — 10 см.
Розв’язання
1) V = 10 см • 10 см • 10 см = 1000 см3 – об'єм куба.
2) S = a • b = 8 см • 25 см = 200 см2 – площа основи прямокутного паралелепіпеда.
3) c = V : S = 1000 см3 : 200 см2 = 5 см – висота прямокутного паралелепіпеда.
4) 200 см2 • 2 + (8 см • 5 см) • 2 + (25 см • 5 см) • 2 = 730 см2 – площа поверхні прямокутного паралелепіпеда.
Відповідь: 730 см2.
Вправа 686 Ребро одного куба в 4 рази більше за ребро другого. У скільки разів:
1) площа поверхні першого куба більша за площу поверхні другого;
Розв’язання
Нехай х – ребро другого куба, тоді х2 – площа грані другого куба, 6х2 – площа поверхні другого куба. Тоді 4х – ребро першого куба, 4х • 4х = 16х2 – площа грані першого куба, 6 • 16х2 = 96х2 – площа поверхні першого куба.
96х2 : х2 = 96 (разів) – у стільки разів площа поверхні першого куба більша, ніж другого куба.
Відповідь: площа поверхні першого куба в 96 разів більша, ніж другого куба.
2) об’єм першого куба більший за об’єм другого?
Розв’язання
Нехай х – ребро другого куба, х3 – об’єм другого куба. Тоді 4х – ребро першого куба, 4х • 4х • 4х = 64х3 – об’єм першого куба.
64х3 : х3 = 64 (разів) – у стільки разів об’єм першого куба більший, ніж другого куба.
Відповідь: об’єм першого куба у 64 рази більший, ніж другого куба.
Вправа 687 Як зміниться об’єм прямокутного паралелепіпеда, якщо:
1) довжину збільшити в 4 рази, ширину — у 2 рази, висоту — у 5 разів;
Збільшиться у 4 • 2 • 5 = 40 разів.
V1 = аbc, V2 = 4а • 2b • 5c = 40аbc = 40V1
2) ширину зменшити в 4 рази, висоту — у 2 рази, а довжину збільшити в 16 разів?
Збільшиться у 16 : 4 : 2 = 2 рази.
V1 = аbc, V2 = 16а • b : 4 • c : 2 = 2аbc = 2V1.
Вправа 688 Як зміниться об’єм прямокутного паралелепіпеда, якщо:
1) кожний вимір збільшити у 2 рази;
Збільшиться в 2 • 2 • 2 = 8 разів.
V1 = аbс, V2 = 2а • 2b • 2с = 8аbс = 8V1).
2) довжину зменшити в 3 рази, висоту — у 5 разів, а ширину збільшити в 15 разів?
Не зміниться.
V1 = аbс, V2 = b • 15 • а : 3 • с : 5 = аbс = V1).
Вправа 689 У басейн, площа дна якого дорівнює 1 га, налили 1 000 000 л води. Чи можна в цьому басейні провести змагання з плавання?
Короткий запис
S = 1000000 дм2
V = 1000000 дм3
h - ?
Розв’язання
1 га = 10000 м2 = 1000000 дм2
1 л = 1 дм3
1 000 000 л = 1 000 000 дм3
h = V : S = 1000000 дм3 : 1000000 дм2 = 1 дм – висота об’єму, що займає вода.
Відповідь: у басейні, де вода налита до 1 дм, плавати не можна.
Вправа 690
В акваріум, що має форму прямокутного паралелепіпеда завдовжки 60 см та завширшки 30 см, налили 8 відер води, у кожному з яких було 9 л. Яка глибина води в акваріумі?
Розв’язання
1) 60 • 30 = 1800 (см2) = 18 (дм2) – площа основи акваріума.
2) 9 • 8 = 72 (л) = 72 (дм5) – об'єм води.
3) 72 : 18 = 4 (дм) = 40 (см) – глибина води в акваріумі.
Відповідь: 40 см.
Вправа 691 У кубі, ребро якого дорівнює З см, зробили три наскрізних квадратних отвори зі стороною 1 см (рис. 180). Знайдіть об’єм частини, що залишилась.
Розв’язання
1) 33 = 27 (см3) – об’єм великого куба.
2) 3 + 2 + 2 = 7 (шт.) – кубиків вирізали.
3) 1 см3 • 7 = 7 см3 – об’єм трьох наскрізних квадратних отвори.
4) 27 – 7 = 20 (см3) – об’єм фігури.
Відповідь: об’єм частини, що залишилась, 20 см3.
Вправи для повторення
Вправа 692 Навігатор показує, що пішоходу до місця призначення залишилося пройти 1200 м, а шлях займе 24 хв. Як зміниться час руху, якщо пішохід збільшить свою швидкість на 10 м/хв?
Розв’язання
1) 1200 : 24 = 50 (м/хв) – початкова швидкість.
2) 50 + 10 = 60 (м/хв) – збільшена швидкість.
3) 1200 : 60 = 20 (хв) – час руху, коли збільшилася швидкості.
4) 24 – 20 = 4 (хв) – на стільки зменшиться час руху, коли збільшилася швидкість.
Відповідь: зменшиться на 4 хв.
Вправа 693 Олена розповіла Івану, що в її саду росте 6 яблунь. Іван сказав, що в нього росте 8 яблунь, а отже, його сім’я збирає більше яблук. Яка сім’я, Олени чи Івана, зібрала більше яблук, якщо в Олени зібрали з кожного дерева 28 кг яблук, а в Івана — 20 кг?
Розв’язання
1) 28 • 6 = 168 (ябл.) – зібрала яблук сім'я Олени.
2) 20 • 8 = 160 (ябл.) – зібрала яблук сім'я Івана.
168 > 160
Відповідь: сім'я Олени зібрала більше яблук.
Вправа 694 Знайдіть значення виразу:
1) якщо а + b = 14, тоді 7а + 7b = 7 (а + b) = 7 • 14 = 98
2) якщо х – у = 4, тоді х • 23 – 23 • у = 23 (х – у) = 23 • 4 = 92
Задача від Мудрої Сови
Вправа 695 Розміри куска мила, що має форму прямокутного паралелепіпеда, дорівнюють 12 см, 6 см і 4 см. Щодня витрачають однакову масу мила. Через 14 днів усі розміри куска мила зменшились у 2 рази. На скільки днів вистачить куска мила, що залишився?
Розв’язання
1) 12 • 6 • 4 = 288 (см3) – об’єм мила спочатку.
2) (12 : 2) • (6 : 2) • (4 : 2) = 6 • 3 • 2 = 36 (см3) – об’єм мила, що залишився.
3) 288 – 36 = 252 (см3) – витратили мила за 14 днів.
4) 252 : 14 = 18 (см3) – витратили мила за 1 день.
5) 36 : 18 = 2 (дні) – днів вистачить.
Відповідь: куска мила, що залишився, вистачить на 2 дні.
Задача 696 У записі одного трицифрового числа використано тільки цифри 2 і 3, а в записі другого — тільки цифри 3 і 4. Чи може добуток цих чисел бути записаним тільки цифрами 2 і 4?
Добуток може закінчуватися цифрою 2, якщо остання цифра першого числа 3, а другого числа – 4, бо 3 • 4 = 12.
Цифрами 2 і 3, щоб остання цифра була 3, можуть бути записані такі трицифрові числа 223, 233, 323.
Цифрами 3 і 4, щоб остання цифра була 4, можуть бути записані такі трицифрові числа 344, 434, 334.
Переберемо добутки цих чисел.
223 • 344 = 76712
223 • 434 = 96782
223 • 334 = 74482
233 • 344 = 80152
233 • 434 = 101122
233 • 334 = 77822
323 • 344 = 111112
323 • 434 = 140182
323 • 334 = 107882
Як бачимо добуток таких чисел не можна бути записаним тільки цифрами 2 і 4.
-------------------------- у підручниках 2013, 2018 років -------------------------------------
Питання
2. Який куб називають одиничним? Куб, ребро якого дорівнює одиничному відрізку, називають одиничним.
Розв’язуємо усно
Завдання 1 Заповніть пропуски в ланцюжку обчислень:
Розв’язання
|
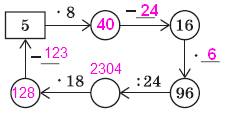
5 • 8 = 40
|
40 – х = 16 х = 40 – 16 х = 24 |
16 • х = 96 х = 96 : 16 х = 6 |
|
х : 24 = 96 х = 96 • 24 х = 2304 |
х • 18 = 2304 х = 2304 : 18 х = 128 |
128 – х = 5 х = 128 – 5 х = 123 |
Завдання 4 Розставте замість зірочок знаки ≪+≫ і ≪-≫ так, щоб запис
20 * З0 * 10 * 80 * 70 = 50 став правильною рівністю.
Розв’язання
20 + 30 – 10 + 80 – 70 = 50
Вправа 626° 1) Скільки сантиметрів в одному дециметрі? квадратних сантиметрів в одному квадратному дециметрі? кубічних сантиметрів в одному кубічному дециметрі?
2) Скільки сантиметрів в одному метрі? Квадратних сантиметрів в одному квадратному метрі? Кубічних сантиметрів в одному кубічному метрі?
Розв’язання
1) 10 см, 100 см2 , 1 000 см3
2) 1 м = 100 см, 10 000 см2, 1 000 000 см3
Вправа 631* Виразіть:
1) у кубічних міліметрах: 38 см3; 42 см3 68 мм3; 35 дм3 67 см3 96 мм3;
2) у кубічних дециметрах: 264 м3; 10 м3 857 дм3; 44 000 см3.
Розв’язання
1) 38 см3 = 38 • 10 мм • 10 мм • 10 мм= 38000 мм3
42 см3 68 мм3 = 42000 мм3 + 68 мм3 = 42068 мм3
35 дм3 67 см3 96 мм3 = 35000000 мм3 + 67000 мм3 + 96 мм3 = 35067096 мм3
2) 264 м3 = 264 • 10 дм • 10 дм • 10 дм = 264000 дм3
10 м3 857 дм3 = 10000 дм3 + 857 дм3 = 10857 дм3
44000 см3 = 44 • 1 дм • 1 дм • 1 дм = 44 дм3
Вправа 632* Виразіть у кубічних сантиметрах: 8 дм3; 378 000 мм3; 8 м3 4 дм3 6 см3.
Розв’язання
8 дм3 = 8 • 10 см • 10 см • 10 см = 8000 см3
378000 мм3 = 378 • 1 см • 1 см • 1 см = 378 см3
8 м3 4 дм3 6 см3 = 8000000 см3 + 4000 см3 + 6 см3 = 8004006 см3
Вправа 642* Знайко сконструював машину, що за 8 год може викопати траншею, яка має форму прямокутного паралелепіпеда і довжина якої дорівнює 150 м, глибина — 80 см, а ширина — 60 см. Скільки кубометрів землі викопує ця машина за 1 год? Роботу скількох коротунів виконує ця машина, якщо за 8 год один коротун може викопати 240 дм3 землі?
Розв’язання
1) 15000 • 80 • 60 = 72000000 (см3) = 72 (м3)
2) 72 : 8 = 9 (м3)
3) 72000 : 240 = 300 (к.)
Відповідь: 300 коротунів.
Вправи для повторення
Вправа 650 З одного міста одночасно в протилежних напрямах виїхали автобус і вантажівка. Через 4 год після початку руху відстань між ними становила 528 км. Швидкість руху автобуса 58 км/год. З якою швидкістю рухалась вантажівка?
Розв’язання
1) 58 • 4 = 232 (км) – відстань автобуса.
2) 528 – 232 = 296 (км) – відстань вантажівки.
3) 296 : 4 = 74 (км/год) – швидкість вантажівки.
Відповідь: вантажівка рухалась зі швидкістю 74 км/год.
Вправа 651 Із двох населених пунктів, відстань між якими дорівнює 54 км, одночасно виїхали назустріч один одному два велосипедисти і зустрілися через 2 год після початку руху. Швидкість руху першого велосипедиста становила 12 км/год. З якою швидкістю рухався другий велосипедист?
Розв’язання
1) 12 • 2 = 24 (км) – відстань першого велосипедиста.
2) 54 – 24 = 30 (км) – відстань другого велосипедиста.
3) 30 : 2 = 15 (км/год) – швидкість другого велосипедиста.
Відповідь: другий велосипедист рухався зі швидкістю 15 км/год.
Вправа 652 Знайдіть значення виразу:
2) якщо m + n = 1000, тоді m • 17 + n • 17 = 17 (m + n) = 17 • 1000 = 17000
3) якщо k + l = 12, тоді k • 9 + 9l = 9 (k + l) = 9 • 12 = 108
4) якщо с – d = 125, тоді 4с – 4d = 4 (с – d) = 4 • 125 = 500
6) якщо р – r = 11, тоді 56 • р – r • 56 = 56 (р – r) = 56 • 11 = 616