
Завдання 666 Поділіть:
|
1) число 138 у відношенні 18 : 5;
Розв'язання
1) 18 + 5 = 23 (ч.) – частин;
2) 138 : 23 = 6 – одна частина;
3) 6 • 18 = 108 – перше число;
4) 6 • 5 = 30 – друге число.
Відповідь: 108 і 30.
|
2) число 70 у відношенні 3 : 6 : 8 : 11.
Розв'язання
1) 3 + 6 + 8 + 11 = 28 (ч.) – частин;
2) 70 : 28 = 2,5 – одна частина;
3) 2,5 • 3 = 7,5 – перше число;
4) 2,5 • 6 = 15 – друге число;
5) 2,5 • 8 = 20 – третє число;
6) 2,5 • 11 = 27,5 – четверте число.
Відповідь: 7,5; 15; 20 і 27,5.
|
Завдання 667
|
1) число 72 у відношенні 7 : 11;
Розв'язання
1) 7 + 11 = 18 (ч.) – частин;
2) 72 : 18 = 4 – одна частина;
3) 4 • 7 = 28 – перше число;
4) 4 • 11 = 44 – друге число.
Відповідь: 28 і 44.
|
2) число 92 у відношенні 2 : 3 : 5.
Розв'язання
1) 2 + 3 + 5 = 10 (ч.) – частин;
2) 92 : 10 = 9,2 – одна частина;
3) 9,2 • 2 = 18,4 – перше число;
4) 9,2 • 3 = 27,6 – друге число;
5) 9,2 • 5 = 46 – третє число.
Відповідь: 18,4; 27,6 і 46.
|
Завдання 668
Для приготування сольового розчину беруть 3 частини солі та 14 частин води. Скільки грамів солі потрібно взяти, щоб приготувати 85 г розчину?
Розв'язання
1) 3 + 14 = 17 (ч.) – частин;
2) 85 : 17 = 5 (г) – маса 1 частини;
3) 5 • 3 = 15 (г) – треба взяти солі.
Відповідь: 15 г.
Завдання 669
Катерина полюбляє напій, настояний на суміші чорного чаю та м’яти. Для цього вона змішує 3 частини чаю і 2 частини м'яти. Скільки грамів м'яти їй потрібно взяти, щоб приготувати 180 г суміші?
Розв'язання
1) 3 + 2 = 5 (ч.) – частин;
2) 180 : 5 = 36 (г) – маса 1 частини;
3) 36 • 2 = 72 (г) – потрібно взяти м'яти.
Відповідь: 72 г.
Завдання 670
Для виготовлення соку ведмежата Гаммі беруть 12 частин ягід і 17 частин води (усі частини мають однакову масу). Скільки кілограмів ягід треба взяти ведмежатам Гаммі, щоб отримати 232 кг соку?
Розв'язання
1) 12 + 17 = 29 (ч.) – частин;
2) 232 : 29 = 8 (кг) – маса 1 частини;
3) 8 • 12 = 96 (кг) – потрібно взяти ягід.
Відповідь: 96 кг.
Завдання 671
Для приготування полуничного варення Антону знадобиться 7 частин ягід і 5 частин цукру (усі частини мають однакову масу). Скільки грамів цукру потрібно взяти Антонові, щоб зварити 2 кг 400 г варення?
Розв'язання
2 кг 400 г = 2400 г
1) 7 + 5 = 12 (ч.) – частин;
2) 2400 : 12 = 200 (г) – маса 1 частини;
3) 200 • 5 = 1000 (г) = 1 (кг) – потрібно взяти цукру.
Відповідь: 1 кг.
Завдання 672
Периметр трикутника дорівнює 48 см, а його сторони відносяться як 7 : 9 : 8. Знайдіть сторони трикутника.
Розв'язання
1) 7 + 9 + 8 = 24 (ч.) – частин;
2) 48 : 24 = 2 (см) – довжина 1 частини;
3) 2 • 4 = 14 (см) – перша сторона;
4) 2 • 9 = 18 (см) – друга сторона;
5) 2 • 8 = 16 (см) – третя сторона.
Відповідь: 14 см; 18 см і 16 см.
Завдання 673
Сторони трикутника відносяться як 5 : 7 : 11, а сума найбільшої і найменшої сторін дорівнює 80 см. Обчисліть периметр трикутника.
Розв'язання
1) 5 + 11 = 16 (ч.) – частин найбільшої і найменшої сторін разом;
2) 80 : 16 = 5 (см) – довжина 1 частини;
3) 5 + 7 + 11 = 23 (см) – всього частин;
4) 5 • 23 = 115 (см) – периметр прямокутника.
Відповідь: 115 см.
Завдання 674
Накресліть розгорнутий кут ABC і проведіть промінь BD так, щоб градусні міри кутів ABD і CBD відносились як 5 : 13.
Розв'язання
1) 5 + 13 = 18 (ч.) – всього частин;
2) 180° : 18 = 10° – міра 1 частини;
3) 10° • 5 = 50° – міра кута ABD;
4) 10° • 13 = 130° – міра кута CBD.
Відповідь: 50° і 130°.
Завдання 675
Накресліть кут MKE, градусна міра якого дорівнює 130°. Між сторонами цього кута проведіть промінь KO так, щоб градусні міри кутів MKO і EKO відносились як 19 : 7.
Розв'язання
1) 19 + 7 = 26 (ч.) – всього частин;
2) 130° : 26 = 5° – міра 1 частини;
3) 5° • 19 = 95° – міра кута MKO;
4) 5° • 7 = 35° – міра кута EKO.
Відповідь: 95° і 35°.
Завдання 676
Площу землі фермерського господарства розподілено між зерновими та овочевими культурами у відношенні 17 : 8. Скільки відсотків площі землі господарства становить площа землі, відведеної під овочеві культури?
Розв'язання
1) 17 + 8 = 25 (ч.) – всього частин;
2) 100% : 25 = 4% – становить 1 частина;
3) 4° • 17 = 68° – становлять площі під зернові культури;
4) 4° • 8 = 32° – становлять площі під овочеві культури.
Відповідь: 68° і 32°.
Завдання 677
У парку відпочинку для продажу заготували деяку кількість повітряних кульок трьох кольорів — синього, рожевого та жовтого, кількості яких відносяться як 9 : 5 : 6 відповідно. Скільки відсотків від кількості всіх кульок становлять жовті?
Розв'язання
1) 9 + 5 + 6 = 20 (ч.) – всього частин;
2) 100% : 20 = 5% – становить 1 частина;
3) 5° • 9 = 45° – становлять сині кульки;
4) 5° • 5 = 25° – становлять рожеві кульки;
5) 5° • 6 = 30° – становлять жовті кульки.
Відповідь: 45°; 25° і 30°.
Завдання 678
Перша операторка набирає на комп’ютері 12 сторінок за годину, а друга — 15 сторінок. Як розподілити між ними рукопис у 180 сторінок, щоб вони працювали однаковий час?
Розв'язання
1) 12 + 15 = 27 (с.) – всього сторінок;
2) 180 : 27 = 180/27 (с.) – набирають разом за 1 год;
3) 180/27 • 12 = 2160/27 = 80 (с.) – набирає перша операторка;
4) 180/27 • 15 = 2700/27 = 100 (с.) – набирає друга операторка.
Відповідь: 80 сторінок і 100 сторінок.
Завдання 679
Троє мулярів працювали з однаковою продуктивністю й отримали за свою роботу 4000 грн. Скільки гривень має отримати кожний муляр, якщо перший з них працював 16 год, другий — 24 год, а третій — 40 год?
Розв'язання
1) 16 + 24 + 40 = 80 (год) – всього годин;
2) 4000 : 80 = 50 (грн) – отримують разом за 1 год;
3) 50 • 16 = 800 (грн) – отримає перший муляр;
4) 50 • 24 = 1200 (грн) – отримає другий муляр;
5) 50 • 40 = 2000 (грн) – отримає третій муляр.
Відповідь: 800 гре; 1200 грн і 2000 грн.
Завдання 680
Як треба поділити 540 т сіна між трьома фермами, якщо на першій фермі 28 корів, на другій — 42 корови, а на третій — 65 корів (потрібна однакова кількість сіна для кожної корови)?
Розв'язання
1) 28 + 42 + 65 = 135 (к.) – всього корів;
2) 540 : 135 = 4 (т) – потрібно для кожної корови;
3) 4 • 28 = 112 (т) – отримає перша ферма;
4) 4 • 42 = 168 (грн) – отримає друга ферма;
5) 4 • 65 = 260 (грн) – отримає третя ферма.
Відповідь: 112 т; 168 т і 260 т.
Завдання 681
Знайдіть такі значення x і y, щоб числа x, y і 24 були відповідно пропорційні числам:
|
1) 3, 5 і 6;
х/3 = у/5 = 24/6
х/3 = у/5 = 4
х/3 = 4, звідси х = 4 • 3 = 12
у/5 = 4, звідси у = 4 • 5 = 20
|
2) 1/8, 1/36 і 1/9.
х : 1/8 = у : 1/36 = 24 : 1/9
8х = 36у = 216,
8х = 216, звідси х = 216 : 8 = 27
36у = 216, звідси у = 216 : 36 = 6
|
Завдання 682
Знайдіть такі значення a і b, щоб числа a, 10 і b були відповідно пропорційні числам 2, 1/6 і 3/4.
а : 2 = 10 : 1/6 = b : 3/4
а : 2 = 60 = b : 3/4
а : 2 = 60, звідси а = 2 • 60 = 120
b : 3/4 = 60, звідси 4b/3 = 60, тому b = 60 • 3 : 4 = 45
Завдання 683
Подайте число 219 у вигляді суми трьох доданків x, y і z так, щоб
x : y = 4 : 9, а y : z = 15 : 2 2/3
Виразимо у всіх відношеннях змінну у.
4y = 9x, звідси x = 4/9 y
15z = 2 2/3 y, звідси z = 8/3 y : 15 = 8/3 y • 1/15 = 8/45 y
Складаємо рівняння і розв'язуємо його:
4/9 y + y + 8/45 y = 219
20/45 y + y + 8/45 y = 219
73/45 y = 219
y = 219 : 73/45
y = 219 • 45/73
y = 135
x = 4/9 • 135 = 60
z = 8/45 • 135 = 34
Відповідь: 135; 60; 34.
Завдання 683
Подайте число 219 у вигляді суми трьох доданків x, y і z так, щоб
x : y = 4 : 9, а y : z = 15 : 2 2/3
Нехай дано чотири числа a, b, c, d. Запишемо їхні відношення:
a : b = 2 : 5; b : c = 3 : 4; c : d = 6 : 7
Виразимо у всіх відношеннях змінну b.
5a = 2b, звідси a = 2/5 b
3c = 4b, звідси c = 4/3 b = 1 1/3 b
6d = 7c, звідси d = 7/6 c = 7/6 • 4/3 b = 7/3 • 2/3 b = 14/9 b = 1 5/9 b
Складаємо рівняння і розв'язуємо його:
2/5 b + b + 1 1/3 b + 1 5/9 b = 386
18/45 b + b + 1 15/45 b + 1 25/45 b = 386
4 13/45 b = 386
b = 386 : 4 13/45
b = 386 : 193/45
b = 386 • 45/193
b = 90
a = 2/5 • 90 = 36
c = 4/3 • 90 =120
d = 14/9 • 90 = 140
Відповідь: 36; 90; 120 і 140.
Вправи для повторення
Завдання 685
Перша бригада відремонтувала 20 км дороги, а друга — 14 км. На скільки відсотків довжини дороги друга бригада відремонтувала менше, ніж перша?
Розв'язання
1) 20 – 14 = 6 (км) – на стільки менше відремонтували;
2) 6 : 20 • 100% = 30%
Відповідь: на 30% менше.
Завдання 686 Перетворення дробів
(1 1/12 + 1 1/4) • 1 10/56 + 2 5/8 • 1 3/7 • 1 1/9 = 7 7/24
1) 1 1/12 + 1 1/4 = 1 1/12 + 1 3/12 = 2 4/12 = 2 1/3
2) 2 1/3 • 1 19/56 = 7/3 • 75/56 = 25/8 = 3 1/8
3) 2 5/8 • 1 3/7 • 1 1/9 = 21/8 • 10/7 • 10/9 = 25/6 = 4 1/6
4) 3 1/8 + 4 1/6 = 3 3/24 + 4 4/24 = 7 7/24
Завдання 687
Накресліть пряму й позначте на ній довільну точку O. Знайдіть на прямій усі точки, які віддалені від точки O на 3 см. ОА = ОВ = 3 см
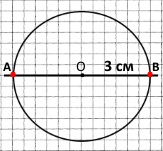
Завдання 688
Позначте на площині довільну точку O. Позначте чотири точки, які віддалені від точки O на 2 см.
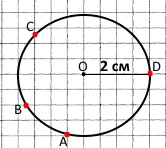
ОА = ОВ = ОС = ОD = 2 см.
Скільки ще можна позначити таких точок? Таких точок на площині безліч. Вони лежать на колі радіусом 2 см.
Задача від Мудрої Сови
Завдання 689
На дошці записано число 23. Щохвилини число стирають і записують на його місце нове число, яке дорівнює добутку цифр старого числа, збільшеному на 12. Яке число буде записано на дошці через годину?
Розв'язання
1) 2 • 3 + 12 = 18 – число з'явиться після першої хвилини;
2) 1 • 8 + 12 = 20 – число з'явиться після другої хвилини;
3) 2 • 0 + 12 = 12 – число з'явиться після третьої хвилини;
4) 1 • 2 + 12 = 14 – число з'явиться після четвертої хвилини;
5) 1 • 4 + 12 = 16 – число з'явиться після п'ятої хвилини.
Оскільки 1 • 6 + 12 = 18, то отримана послідовність чисел є періодичною з періодом 5, тобто після кожної п'ятої хвилини на дошці буде з'являтися число 16, тому за годину на дошці буде записане число 16.
Відповідь: 16.