Розв'язуємо усно
|
1) 4
|
2) 1,2
|
3) −18
|
4) 4
|
5) −0,91
|
6) 1
|
|
1) 7х + 1 = 5х − 9
7х − 5х = −9 − 1
2х = −10
х = −10 : 2
х = −5
|
2) 14а = 8а − 5,4
14а − 8а = −5,4
6а = −5,4
а = −5,4 : 6
а = −0,9
|
Завдання 1223 Координати точок
A(З;2); В(–1;4); С(–6;2); D(–5;–2); Е(2;–2); F(0;3); К(4;0); М(–2;–4); N(5;4)
Завдання 1224
А(2;2); В(5;1); С(0;–5); D(2;–3); Е(–1;–1); F(–5;0); K(–4;3); М(–3;2); N(–4;–3)
Завдання 1225 Координатна площина
Точки: A(2;3), B(4;–5), C(–3;7), D(–2;2), F(–4;–2), K(2;–2), M(0;2), N(–3;0), P(1;–6)
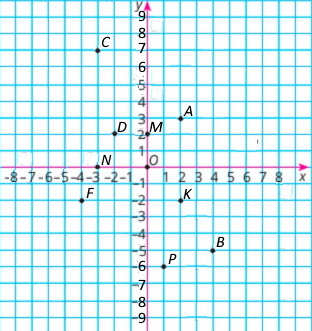
Завдання 1226
Точки: A(5;1), B(2;–1), C(–7;–1), D(–5;3), E(1;0), F(0;–4), S(–1;–3), T(–6;2), Q(3;2)
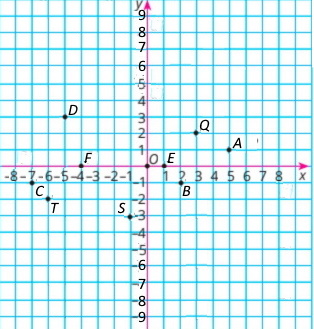
Завдання 1227
Відрізки AB і CD, якщо A(–1;–3), B(3;1), C(0;4), D(3;–2)
Координата точки перетину цих відрізків: К(2:0)
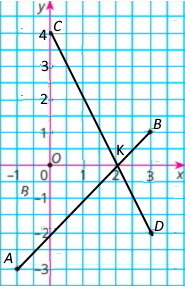
Завдання 1228
Відрізки AB і CD, якщо A(–5;–2), B(1;4), C(–3;2), D(2;–3)
Координати точки перетину цих відрізків: B(–2;1)
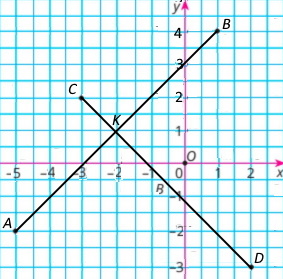
Завдання 1229
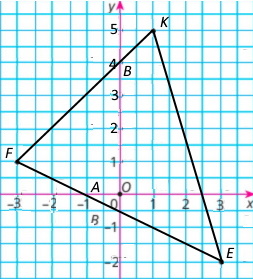
Трикутник EFK, якщо E(3;–2), F(–3;1), K(1;5).
Координати точки перетину сторони EF з віссю x: А(–1;0)
Координати точки перетину сторони FK з віссю y: В(0;4)
Завдання 1230
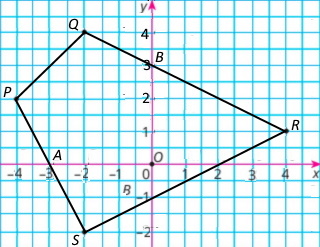
Чотирикутник PQRS, якщо P(–4;2), Q(–2;4), R(4;1), S(–2;–2)
Координати точки перетину сторони QR з віссю y: В(0;3)
Координати точки перетину сторони PS з віссю x: P(–3;0)
Завдання 1231
Дано координати трьох вершин прямокутника ABCD: A(–3;–1), B(–3;3) і D(5;–1)
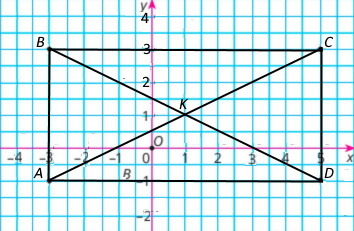
2) Координати вершини C(5;3)
3) Координати точки перетину діагоналей прямокутника K(1;1)
4) Обчисліть площу та периметр прямокутника, вважаючи, що довжина одиничного відрізка координатних осей дорівнює 1 см.
Завдання 1232, 1233, 1234
|
1) Ординати: 4; –1; 0 2) Абсциси: 1; –1; –4 |
1) Ординати: 0; ±3 2) Абсциси: 0; ±4; ±5 |
1) Ординати: 0; 5; –3 2) Абсциси: 0; ±1; ±2 |
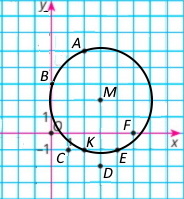
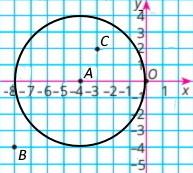
Коло із центром у точці M(3;2), яке проходить через точку K(2;–1).
З точок A(2;5), B(0;3), C(1;–1), D(3;–2), E(4;–1), F(5;0) належать колу точки: А; В; К; Е.
Завдання 1236
Коло із центром у точці A (–4;0), яке проходить через початок координат.
Радіус цього кола дорівнює 4 одиничним відрізкам.
Координата точки, яка належить кругу, обмеженого цим колом: С(–3;1)
Координата точки, яка лежить поза кругом, обмеженого цим колом: В(–8;–4)
Завдання 1237
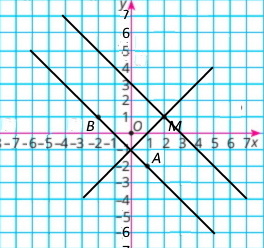
Позначте на координатній площині точки M (2;1), A(1;–2) і B(–2;1). Проведіть пряму AB. Через точку M проведіть пряму, паралельну прямій AB, і пряму, перпендикулярну до прямої AB.
Завдання 1238
|
Точка A (x ; y), якщо |
|
|
1) x > 0, y > 0; І чверть 2) x > 0, y < 0; III чверть |
3) x < 0, y < 0; IV чверть 4) x < 0, y > 0? II чверть |
|
Вище чи нижче від осі x розміщена точка B (x ; y), якщо:
|
|
|
1) y > 0, x — довільне число; Вище
|
2) y < 0, x — довільне число? Нижче
|
Завдання 1240
|
Праворуч чи ліворуч від осі y розміщена точка C (x ; y), якщо:
|
|
|
1) x < 0, y — довільне число; Ліворуч
|
2) x > 0, y — довільне число? Праворуч
|
Завдання 1241
1) вище осі x лежать точки: A(2;4), F(0;7), S(–9;7)
3) на осі x: E(47;0), P(–6;0)
2) ліворуч від осі y: D(–4;–50), Q(–1;–1), S(–9;7), P(–6;0)
4) на осі y: C (0;–20), F (0;7)
Завдання 1242
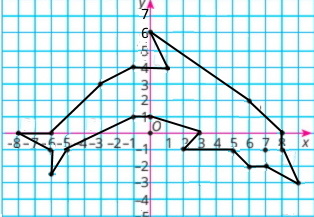
Накресліть на координатній площині замкнену ламану, послідовними вершинами якої є точки з координатами: (8;0), (6;2), (0;6), (1;4), (–1;4), (–3;3), (–6;0), (–8;0), (–6;–1), (–6;–2,5), (–5;–1), (–1;1), (0;1), (3;0), (2;–1), (5;–1), (6;–2), (7;–2), (9;–3), (8;–1).
Точка (7;–1) - око риби.
Завдання 1243
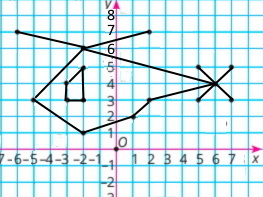
Накресліть на координатній площині дві замкнені ламані, послідовними вершинами яких є точки з координатами: (–5;3), (–2;1), (1;2), (2;3), (6;4), (–2;6) і (–3;3), (–3;4), (–2;5), (–2;3); чотири відрізки з кінцями в точках (–6;7) і (–2;6); (2;7) і (–2;6); (5;3) і (7;5); (5;5) і (7;3).
Завдання 1244
|
1) x = –3, y — довільне число; |
2) y = –5, x — довільне число. |
|
|
|
Завдання 1245
|
1) x = 4, y — довільне число; |
2) y = 2, x — довільне число. |
|
|
|
|
1) абсциса й ордината рівні; |
2) абсциса й ордината — протилежні числа. |
|
|
|
|
1) у = 0, х < 3; |
2) –4 < y < 4, x ≥ 0; |
|
|
|
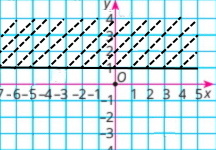
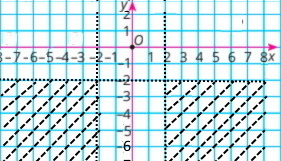
| 3) |х| ≤ –1, у ≥ 1; | 4) |x| > 2, y < –2 |
 |
 |
Завдання 1248
|
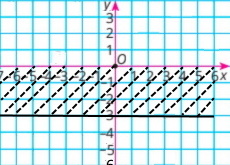
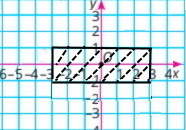
1) х = 0, у ≥ –3;
|
2) –2 ≤ х ≤ 3, у — довільне число;
|
 |
 |
|
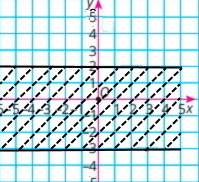
3) |у| ≤ 2, х – довільне число;
|
4) |х| ≤ 3, |у| ≤ 1.
|
 |
 |
Вправи для повторення
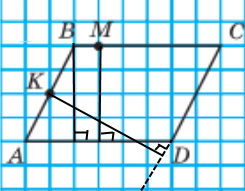
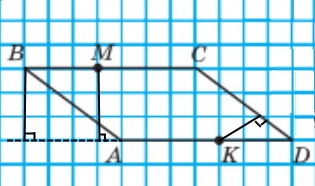
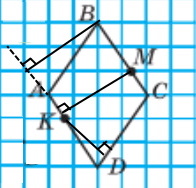
Завдання 1249
Провели через кожну з точок B і M пряму, перпендикулярну до прямої AD, а через точку K — пряму, перпендикулярну до прямої CD.
 |
 |
 |
Свіжі яблука містять 75% води, а сушені — 12 %. Скільки кілограмів сушених яблук вийде з 264 кг свіжих?
Розв'язання
1) 100% – 75% = 25% – яблука без води у свіжих яблуках;
2) 264 кг — 100%
х кг — 25%
264/х = 100/25; х = 25 • 264 : 100; х = 66 (кг) – чисто яблука у свіжих яблуках;
3) 100% – 12% = 88% – яблука без води в сушених яблуках;
4) х кг — 100%
66 кг — 88%
х/66 = 100/88; х = 100 • 66 : 88; х = 75 (кг) – чисто яблука у сушених яблуках.
Відповідь: 75 кг.
Завдання 1251
Білочка вирішила перевірити свій запас горішків. Коли вона рахувала їх десятками, то не вистачило 2 горішків до цілого числа десятків, а коли почала рахувати дюжинами, то залишилося 8 горішків. Скільки горішків було в білочки, якщо відомо, що їх більше за 300, але менше від 350?
Міркуємо так. Число одиниць кількості горішків дорівнює 8. Шукане число при діленні на 12 має давати остачу 4 і закінчуватися на 8. З чисел у межах від 301 до 349 таку властивість має тільки число 308, бо 308 = 25 • 12 + 8. Отже, у білочки було 308 горішків.
Завдання 1252
На торговельній базі цукор–пісок розфасовано в кілограмові, трикілограмові та десятикілограмові пакети. Кілограмовий пакет коштує 30 грн, трикілограмовий — 84 грн, а десятикілограмовий — 270 грн. Потрібно придбати 45 кг цукру–піску. Знайдіть найвигідніший варіант купівлі цукру й обчисліть його вартість.
Розв'язання
1) 270 : 10 = 27 (грн) – ціна цукру в 10–кілограмовому мішку;
2) 84 : 3 = 28 (грн) – ціна цукру в 3–кілограмовому мішку;
тоді, найвигідніший варіант: 4 • 10 кг + 3 кг + 2 • 1 кг = 45 кг.
3) 4 • 270 + 84 + 2 • 30 = 1080 + 84 + 60 = 1224 (грн) – вартість цукру.
Відповідь: 1224 грн.
Завдання 1253
Для перевезення 30 т вантажу на відстань 80 км можна скористатися послугами однієї з трьох фірмперевізників. Вартість перевезення та вантажопідйомність автомобілів кожної фірми наведено в таблиці. Скільки гривень коштуватиме найдешевше перевезення вантажу?
|
Фірма–перевізник |
Вартість перевезення одним автомобілем на 10 км, грн |
Вантажопідйомність автомобіля, т |
|
А |
210 |
4 |
|
Б |
240 |
5,5 |
|
В |
360 | 10 |
1) 210 : 4 = 52,5 (грн) – вартість перевезення 1 т перевізником А;
2) 240 : 5,5 = 43,(63) (грн) – вартість перевезення 1 т перевізником Б;
3) 360 : 10 = 36 (грн) – вартість перевезення 1 т перевізником В;
4) (30 : 10) • (80 : 10) • 360 = 3 • 8 • 360 = 8640 (грн) – вартість найдешевшого перевезення.
Відповідь: 8640 грн, перевізником В найдешевше перевезення.
Задача від Мудрої Сови
Завдання 1254
В одній купці лежить 171 камінець, а в другій — 172 камінці. За один хід дозволяється брати будь–яку кількість камінців, але тільки з однієї купки. Програє той, кому не буде чого брати. Хто виграє за правильної стратегії — той, хто починає, чи інший гравець?
Виграє той, що починає, тобто перший гравець. Для цього йому достатньо під час першого свого ходу вирівняти купки, взявши з більшої один камінець, а потім дотримуватися симетричної стратегії, тобто, якщо другий гравець візьме певну кількість камінців з однієї купки, то першому слід взяти таку саму кількість камінців з другої купки.