Завдання 1. Скільки різних чотирицифрових чисел можна скласти із цифр 5, 6, 7, 8, 9 так, щоб у кожному числі не було однакових цифр?
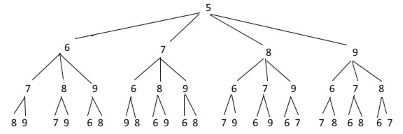
Маємо 24 чотирицифрових числа з цифр 5, 6, 7, 8, 9 (цифри не повторюються), які починаються цифрою 5:
5678, 5679, 5687, 5689, 5696, 5698;
5769, 5768, 5786, 5789, 5796, 5798;
5867, 5879, 5876, 5879, 5896, 5897;
5967, 5968, 5976, 5978, 5986, 5987.
1 рівень графа 1 цифра
2 рівень графа 1 • (5 – 1) = 4 цифри
3 рівень графа 4 • (5 – 2) = 12 цифр
4 рівень графа 12 • (5 – 3) = 24 цифри
Формула графа (5 – 1) • (5 – 2) • (5 – 3) = 24
З одною цифрою маємо 24 комбінації, з 5 такими цифрами будемо мати
5 • (5 – 1) • (5 – 2) • (5 – 3) = 5 • 24 = 120 комбінацій чотирицифрових чисел.
Відповідь: з 5 цифр можна скласти 120 чотирицифрових чисел.
Щоб знайти кількість двоцифрових чисел з n цифр (цифри не повинні повторюватися і серед них нема цифри 0) маємо формулу:
n • (n – 1), де n – кількість цифр, з яких треба побудувати двоцифрове число.
Щоб знайти кількість трицифрових чисел з n цифр (цифри не повинні повторюватися і серед них нема цифри 0) маємо формулу:
n • (n – 1) • (n – 2), де n – кількість цифр, з яких треба побудувати трицифрове число.
Щоб знайти кількість чотирицифрових чисел з n цифр (цифри не повинні повторюватися і серед них нема цифри 0) маємо формулу:
n • (n – 1) • (n – 2) • (n – 3), де n – кількість цифр, з яких треба побудувати чотирицифрове число.
Змінимо умову задачі так, щоб була цифра 0.
Завдання 2. Скільки різних чотирицифрових чисел можна скласти із цифр 5, 6, 7, 0, 9 так, щоб у кожному числі не було однакових цифр?
Аналогічно для числа, яке починається, наприклад, цифрою 5, маємо 24 чотирицифрових числа.
З одною цифрою маємо 24 комбінації. Оскільки число не може починатися нулем, то з 4 різними початковими цифрами будемо мати
4 • (5 – 1) • (5 – 2) • (5 – 3) = 4 • 24 = 96 комбінацій чотирицифрових чисел.
Відповідь: з 5 цифр, коли серед них є цифра 0, можна скласти 96 чотирицифрових чисел.
Щоб знайти кількість двоцифрових чисел з n цифр (цифри не повинні повторюватися, серед них є цифра 0) маємо формулу:
(n – 1) • (n – 1) = (n – 1)2 , де n – кількість цифр, з яких треба побудувати двоцифрове число.
Щоб знайти кількість трицифрових чисел з n цифр (цифри не повинні повторюватися, серед них є цифра 0) маємо формулу:
(n – 1) • (n – 1) • (n – 2) = (n – 1)2 • (n – 2), де n – кількість цифр, з яких треба побудувати трицифрове число.
Щоб знайти кількість чотирицифрових чисел з n цифр (цифри не повинні повторюватися, серед них є цифра 0) маємо формулу:
(n – 1) • (n – 1) • (n – 2) • (n – 3) = (n – 1)2 • (n – 2) • (n – 3), де n – кількість цифр, з яких треба побудувати чотирицифрове число.
ВИСНОВОК. Якщо треба порахувати кількість чисел, використовуємо формулу.
Якщо треба написати такі числа, використовуємо граф.