Властивість фігури – це певна якість, ознака, характерна фігурі.
Геометрія як наука вивчає властивості фігур.
ВЛАСТИВІСТЬ ВІДРІЗКІВ
◊ Основна властивість відрізка.
Кожний відрізок має певну довжину, більшу за нуль.
◊ Основна властивість вимірювання відрізків.
Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його внутрішньою точкою.
![]()
ВЛАСТИВІСТЬ КУТІВ
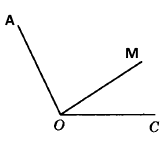
◊ Основна властивість вимірювання кутів.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
∠AOC = ∠AOM + ∠MOC
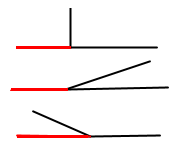
◊ Властивість суміжних кутів.
Сума суміжних кутів дорівнює 180°.
∠1 + ∠2 = 180°
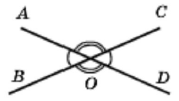
◊ Властивість вертикальних кутів.
Вертикальні кути рівні.
∠AOB = ∠COD, ∠AOC = ∠BOD
ВЛАСТИВІСТЬ ПРЯМОЇ
◊ Основна властивість прямої.
Через дві точки можна провести пряму і до того тільки одну.

ВЛАСТИВІСТЬ ПАРАЛЕЛЬНИХ ПРЯМИХ
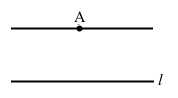
◊ Аксіома про основну властивість паралельних прямих.
Через точку, що не лежить на даній прямій, проходить тільки одна пряма, паралельна даній.
◊ Властивість паралельних прямих.
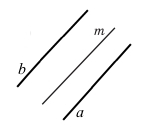
Дві прямі, паралельні третій прямі, паралельні одна одній.
Якщо а || m і b || m, тоді a || b.
◊ Властивість відповідних кутів, що утворилися при перетині паралельних прямих січною.
Відповідні кути, що утворилися при перетині паралельних прямих січною, рівні між собою.
Відповідні кути: ∠2 = ∠6; ∠3 = ∠7; ∠1 = ∠5; ∠4 = ∠8.
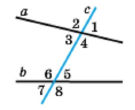
◊ Властивість внутрішніх різносторонніх кутів, утворених при перетині паралельних прямих січною.
Внутрішні різносторонні кути, утворені при перетині паралельних прямих січною, рівні між собою.
Внутрішні різносторонні кути: ∠3 = ∠5; ∠6 = ∠4.

◊ Властивість внутрішніх односторонніх кутів, утворених при перетині паралельних прямих січною.
Сума внутрішніх односторонніх кутів, утворених при перетині паралельних прямих січною, дорівнює 180°.
Для внутрішніх односторонніх кутів ∠3 + ∠6 = 180°; ∠4 + ∠5 = 180°.
