Зовнішній кут трикутника — кут, суміжний з кутом цього трикутника.
∠1, ∠2, ∠3 – зовнішні кути трикутника.
Суміжний кут трикутника зазвичай можуть називати внутрішнім.
∠4, ∠5, ∠6 – внутрішні кути трикутника.
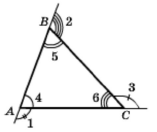
∠1 — зовнішній для кута ∠4. ∠1 + ∠4 = 180°
∠2 — зовнішній для кута ∠5. ∠2 + ∠5 = 180°
∠3 — зовнішній для кута ∠6. ∠3 + ∠6 = 180°
◊ Теорема (властивість зовнішнього кута трикутника).
Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним.
∠1 — зовнішній для кута ∠4. ∠1 = ∠5 + ∠6
∠2 — зовнішній для кута ∠5. ∠2 = ∠4 + ∠6
∠3 — зовнішній для кута ∠6. ∠3 = ∠5 + ∠4
Наслідок. Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний з ним.
∠1 — зовнішній для кута ∠4. ∠1 > ∠5 і ∠1 > ∠6
∠2 — зовнішній для кута ∠5. ∠2 > ∠4 і ∠2 > ∠6
∠3 — зовнішній для кута ∠6. ∠3 > ∠5 і ∠3 > ∠4
Сума зовнішніх кутів трикутника, узятих по одному, дорівнює 360°.
∠1 — зовнішній для кута ∠4,
∠2 — зовнішній для кута ∠5,
∠3 — зовнішній для кута ∠6.
Знайдемо суму зовнішніх кутів, узятих по одному.
∠1 + ∠2 + ∠3 = (∠5 + ∠6) + (∠4 + ∠6) + (∠5 + ∠4) = 2 • (∠4 + ∠5 + ∠6) = 2 • 180° = 360°
Кожна вершина може мати два однакових зовнішніх кути.
Кожні дві сторони трикутника лежать, на прямих, що перетинаються. Такі прямі утворюють дві пари суміжних кутів.
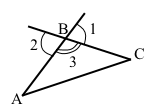
∠1 = ∠2 — зовнішні кути для кута трикутника ∠3.
Т. д. для решти кутів трикутника.