Інші завдання дивись тут...

ПРЯМОКУТНИЙ ТРИКУТНИК – це трикутник, один кут якого прямий.

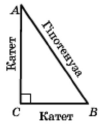
∆АВС – прямокутний, його ∠С = 90°

Сторону прямокут­ного трикутника, яка лежить проти прямого кута, називають гіпотенузою, а дві інші сторони – катетами.

АВ – гіпотенуза, АС і ВС – катети.

ВЛАСТИВОСТІ прямокутних трикутників

Сума гострих кутів прямокутного трикутника дорівнює 90°.

∠А + ∠В = 90°

Це наслідок із теореми про суму кутів трикутників.

Гіпотенуза прямокутного трикутника більша за будь-який катет.

АВ – гіпотенуза, АС і ВС – катети, тоді

АВ > АС  і   АВ > ВС. 

Ця властивість є наслідком теореми про співвідношення між сторонами і кутами трикутника, оскільки прямий кут більший за гострий.

Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.

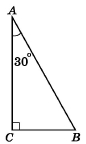
У прямокутному трикутнику АВС  ∠С = 90°, а ∠А = 30°.

Тоді катет СВ = 1/2 АВ. Ще можна записати АВ = 2СВ.

Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то кут, що лежить проти цього катета дорівнює 30°.

У прямокутному трикутнику АВС  ∠С = 90°, СВ = 1/2 АВ (ще можна записати АВ = 2СВ).

Тоді ∠А = 30°

У прямокутному трикутнику медіана, проведена до гіпотенузи, дорівнює половині гіпотенузи.

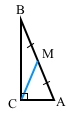
У прямокутному трикутнику АВС  ∠С = 90°, СМ – медіана до гіпотенузи.

Тоді СМ = 1/2 АВ (ще можна записати АВ = 2СМ)

У прямокутному трикутнику середина гіпотенузи рівновіддалена від його вершин.

У прямокутному трикутнику АВС  ∠С = 90°, СМ – медіана до гіпотенузи, МВ = МА. За властивістю медіани прямокутного трикутника СМ = 1/2 АВ.

ВМ = МА = МС = 1/2 АВ

ОЗНАКИ РІВНОСТІ прямокутних трикутників

• Якщо катети одного прямокутного трикутника відповідно дорів­нюють катетам іншого, то такі трикутники рівні між собою.

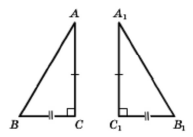
Якщо катети ВС = В₁С₁ і СА = С₁А₁, тоді ∆АВС = ∆А₁В₁С₁. 

Випливає з першої ознаки рівності трикутників (за двома сторонами і кутом між ними)

• Якщо катет і прилеглий до нього гострий кут одного прямокут­ного трикутника відповідно дорівнюють катету і прилеглому до нього куту іншого, то такі трикутники рівні між собою.

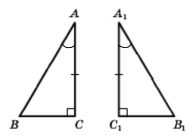
Якщо катети АС = А₁С₁, прилеглі до катетів ∠А = ∠А₁, тоді ∆АВС = ∆А₁В₁С₁. 

Випливає з другої ознаки рівності трикутників (за стороною та прилеглими кутами).

• Якщо гіпотенуза і гострий кут одного прямокутного три­кутника відповідно дорівнюють гіпотенузі й гострому куту іншого, то такі трикутники рівні між собою.

Випливає із властивості гострих кутів (якщо у двох прямокутних трикутників є одна пара рівних між собою гострих кутів, то й інша пара гострих кутів – також рівні між собою кути) і другої  ознаки трикутника (за стороною і прилеглими кутами).

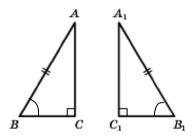
Якщо гіпотенузи АВ = А₁В₁ і гострі кути ∠В = ∠В₁, тоді ∆АВС = ∆А₁В₁С₁. 

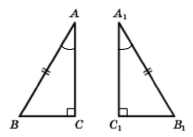
Якщо гіпотенузи АВ = А₁В₁ і гострі кути ∠А = ∠А₁, тоді ∆АВС = ∆А₁В₁С₁. 

• Якщо катет і протилежний йому кут одного прямокутного трикутника відповідно дорівнюють катету і протилежному йому куту іншого, то такі трикутники рівні між собою.  

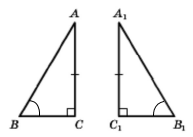
Якщо катети АС = А₁С₁, протилежні до катетів ∠В = ∠В₁, тоді ∆АВС = ∆А₁В₁С₁. 

Випливає із властивості гострих кутів (якщо у двох прямокутних трикутників є одна пара рівних між собою гострих кутів, то й інша пара гострих кутів – також рівні між собою кути) і другої  ознаки трикутника (за стороною і прилеглими кутами).

◊ Теорема (ознака рівності прямокутних трикутників за катетом і гіпотенузою)

Якщо катет і гіпотенуза одного прямокутного трикутника відповідно дорівнюють катету і гіпотенузі іншого, то такі трикутники рівні між собою.

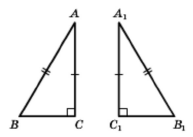
Якщо гіпотенузи АВ = А₁В₁, катети АС = А₁С₁, тоді ∆АВС = ∆А₁В₁С₁

Інші завдання дивись тут...