Інші завдання дивись тут...

КОЛО — геометрична фігура, яка складається з усіх точок площини, рівновіддалених від даної точки.

Коло на папері зображують за допомогою циркуля, а на місцевості для побудови кола можна використати мотузку.

ЕЛЕМЕНТИ КОЛА

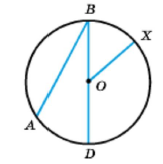
Центр кола — точка, від якої рівновіддалені усіх точки площини кола.

Точка О – центр кола.

Центр кола є серединою будь-якого діаметра, тобто BD = 2ВО = 2ОD.

Радіус — відрізок, що сполучає центр з будь-якою точкою кола.

У колі можна провести безліч радіусів.

Відрізки ОХ, ОВ, ОD – радіуси кола. 

З означення кола випливає, що всі радіуси одного й того самого кола мають однакову довжину.

ОХ = ОВ = OD

Радіус кола зазвичай позначають буквою r.

Радіус – це половина діаметра:   r = d/2.

Хорда — відрізок, що сполучає дві точки кола.

Відрізки АВ, ВD – хорди.

Через одну точку на колі можна провести безліч хорд. 

Через одну точку на колі можна провести тільки дві хорди заданої довжини.

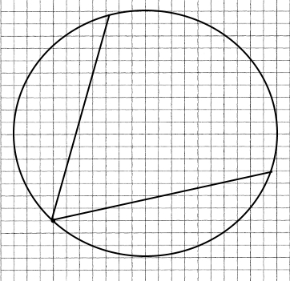
Через дві точки на колі можна провести тільки одну хорду.

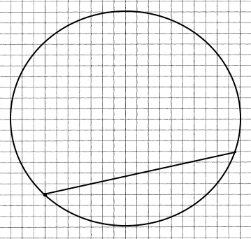
Діаметр — хорда, що проходить через центр кола.

Відрізок BD – діаметр кола.

Через центр кола можна провести безліч радіусів.

Через дві точки кола можна провести тільки один радіус.

Центр кола є серединою будь-якого діаметра, тобто довжина діаметра вдвічі більша за довжину радіуса.

Діаметр кола зазвичай позначають буквою d.

d = 2r.

◊ Теорема 1 (про порівняння діаметра і хорди).

Діаметр є найбільшою з хорд.

Якщо BD – діаметр, а АВ – хорда, яка не є діаметром, тоді АВ < BD або BD > АВ .  

◊ Теорема 2 (про кут, під яким видно діаметр з точки кола).

Діаметр з будь-якої точки кола видно під прямим кутом.

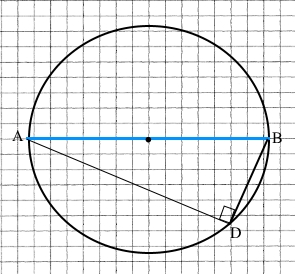
Якщо АВ – діаметр кола, а BD – хорда, яка не є діаметром, тоді ∠АDB = 90°. 

◊ Теорема 3 (властивість діаметра кола, перпендикуляр­ного до хорди).

Діаметр кола, перпендикулярний до хорди, ділить її навпіл.

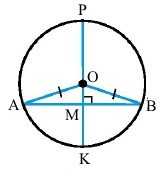
Якщо РК – діаметр кола, відрізок АВ – хорда, яка не є діаметром, РК ﬩ АВ, причому точка М – точка перетину діаметра і хорди, тоді АМ = МВ, ∠РМА = ∠РМВ = 90°. 

◊ Теорема 4 (властивість діаметра кола, що проходить через середину хорди).

Діаметр кола, що проходить через середину хорди, яка не є діаметром, перпендикулярний до цієї хорди.

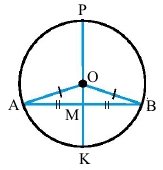
Якщо РК – діаметр кола, відрізок АВ – хорда, яка не є діаметром, причому точка М – його середина (АМ = МВ), тоді РК ﬩ АВ, або ∠РМА = ∠РМВ = 90°.  

Інші завдання дивись тут...