Вписаний кут — кут, вершина якого належить колу, а сторони перетинають коло.
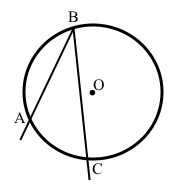
Кут АВС – вписаний у коло з центром О.
Вершина В належить колу, а сторони ВА і ВС кута АВС перетинають коло у точках А і С.
Можливі три випадки розташування центра кола відносно вписаного кута.
• Центр кола – точка О – лежить на одній зі сторін кута.
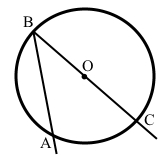
• Центр кола – точка О – лежить усередині вписаного кута.
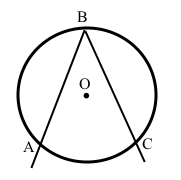
• Центр кола – точка О – лежить зовні вписаного кута.

Дугою, на який спирається вписаний кут, буде та дуга, яка не містить вершини кута В.
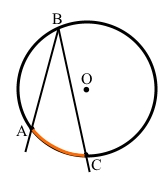
Сторони ВА і ВС кута АВС перетинають коло у точках А і С та ділять коло на дві дуги:
͜ АВС і ͜ АС.
Кажуть, що вписаний кут АВС спирається на дугу AC.
͜ АС – дуга, на яку спирається вписаний кут АВС.
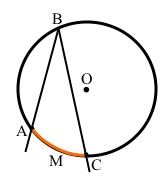
Сторони ВА і ВС кута АВС перетинають коло у точках А і С та ділять коло на дві дуги:
͜ АВС і ͜ АМС.
Кажуть, що вписаний кут АВС спирається на дугу AMC.
͜ АMС – дуга, на яку спирається вписаний кут АВС.
◊ Теорема (про вписаний кут).
Вписаний кут вимірюється половиною дуги, на яку він спирається.

͜ АMС – дуга, на яку спирається вписаний кут АВС, тоді
∠АВС = 1/2 ͜ АMС
Наслідок. Вписані кути, що спираються на одну й ту саму дугу, між собою рівні.
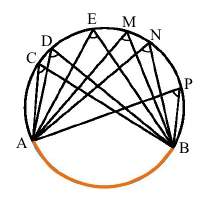
Якщо вписані кути спираються на одну і ту саму дугу ͜ АВ, тоді
∠АСB = ∠АDB = ∠АEB = ∠АMB = ∠АNB = ∠АPВ
Наслідок. Вписаний кут, що спирається на діаметр – прямий.
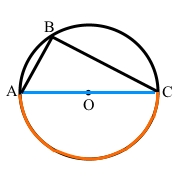
Кут АВС – вписаний кут у коло з центром О, АС – діаметр кола, тоді
∠АВС = 90°.