Завдання 660
Чи залежить периметр квадрата Р від довжини його сторони а? Чи є P функцією від a? Периметр квадрата залежить від довжини його сторони. Периметр квадрата в чотири рази більший від сторони, тому є функцію від довжини сторони квадрата.
Завдання 661
Об’єм куба знаходять за формулою V = a3, де a — довжина ребра куба. Чи задає ця формула функцію? Який її аргумент? Ця формула задає функцію. її аргумент — а.
Завдання 662
Площу круга знаходять за формулою S = πr2. Чи задає ця формула функцію? Яка її область визначення? Формула S = πr2 задає функцію, область визначення якої — всі додатні числа.
Завдання 663
Густина міді — 8,6 г/см3. Вирази формулою відповідність між об’ємом V куска міді та його масою m. Чи є m функцією від V? Який її аргумент? Яка область визначення?
m = 8,6V , де m — маса, V — об'єм; m є функцією від V, аргумент якої V. Області, визначення — всі додатні числа.
Завдання 664
Швидкість автобуса — 55 км/год. Як залежить пройдений автобусом шлях s від часу t? Чи є змінна s функцією від t? S = 55t, де S — пройдений шлях, t — час. Змінна S є функцією від t.
Завдання 665
Площа прямокутника зі сторонами 5 см і x см дорівнює s см2. Чи є змінна s функцією від x? Який її аргумент? S = 5x. Змінна S є функцією від х; її аргумент х.
Завдання 666
Функцію задано формулою у = 3х – 1. Знайди значення функції, що відповідає значенню аргументу –2.
y = 3 • (–2) – 1 = –6 – 1 = –7, тому В –7
Завдання 667
Установи відповідність між значенням аргументу (1–3) та значенням функції (А–Г), заданої формулою у = 4х + 1. 1 – Г; 2 – В; 3 – А.
Завдання 668
Про яку з функцій не можна сказати, що її областю визначення є всі числа? Г у = 12/(12 – х)
Завдання 669
Виразіть формулою відповідність між довжиною a сторони рівностороннього трикутника і його периметром P. Чи є змінна P функцією від a?
Р = 3a. Змінна Р є функцією від а.
Завдання 670
Міри суміжних кутів — α і β. Задай формулою залежність α від β. Чи є α функцією від β? Який її аргумент?
α = 180 – β. α є функцією від β; її аргумент — β.
Завдання 671
Чи залежить діаметр кола d від його радіуса r? Вирази цю залежність формулою.
Діаметр d кола вдвічі більший від радіуса кола, тому d = 2r.
Завдання 672
Відповідність між шістьма першими натуральними числами та їх квадратами зображено на малюнку 16.6. Чи є ця відповідність функцією? Так.
Запиши її:
а) область визначення: 1; 2; 3; 4; 5; 6;
б) область значень: 1; 4; 9; 16; 25; 36.
Завдання 673
На малюнку 16.7 зображено відповідність між числами 1, 2, 3, 4 та оберненими до них числами. Чи є ця відповідність функцією? Так.
Запиши її:
а) область визначення: 1; 2; 3; 4;
б) область значень: 1; 1/2; 1/3; 1/4.
Завдання 674
Функцію задано формулою у = 6/x. Заповни таблицю.
|
х |
–6 |
–3 |
–2 |
–1 |
1 |
2 |
3 |
6 |
|
у |
–1 | –2 | –3 | –6 | 6 | 3 | 2 | 1 |
Завдання 675
The function is given by the formula y = 0,3x. Fill in the table.
|
x |
–10 |
–3 |
–1 |
0 |
4 |
5 |
50 |
|
y |
–3 |
–0,9 |
–0,3 |
0 |
1,2 |
1,5 |
15 |
Завдання 676
Функцію задано формулою у = x² + 3. Склади таблицю її значень для перших десяти натуральних значень її аргументу.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
y |
4 |
7 |
12 |
19 |
28 |
39 |
52 |
67 |
84 |
103 |
Завдання 677
Склади таблицю значень функції m = 42 – 3n для перших десяти натуральних значень змінної n.
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
m |
39 |
36 |
33 |
30 |
27 |
24 |
21 |
18 |
15 |
12 |
Завдання 678
Знайди область визначення функції, заданої формулою:
а) у = 3x – 7; Множина дійсних чисел
б) y = x/(x + 5); Множина дійсних чисел, крім x = –5
в) у = 5x² – x + 3. Множина дійсних чисел
Завдання 679
Учень мав 50 грн. Він купив x наліпок по 6 грн, після чого в нього залишилось у грн. Задайте формулою функцію, яка виражає залежність у від x. Яка її область визначення?
Фукнція: у = 50 – 6х. Область визначення: 50; 44; 38; 32; 26; 20; 14; 8
Завдання 680
Ціна 1 кг товару — 250 грн. Як залежить вартість цього товару у від його маси m? Яка вартість товару, маса якого дорівнює 18 кг? Товар якої маси коштує 125 грн?
z = 250m
Якщо m = 18, тоді z = 250 • 18 = 4500 (грн)
Якщо z = 125, тоді 125 = 250 • m; m = 125/250 = 0,5 (кг)
Завдання 681
Нафта проходить трубою зі швидкістю 12 т/год. Скільки нафти проходить такою трубою за 3 год; за t год? Напиши відповідну формулу.
m = 12t
Якщо t = 3, тоді m = 12 • 3 = 36 (т)
Завдання 682
Скільки хвилин у t год? Вирази цю відповідність формулою. y = 60t
Склади таблицю для 10 значень аргументу.
|
t, год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
8 |
10 |
|
y, хв |
60 |
120 |
180 |
240 |
300 |
360 |
420 |
480 |
540 |
600 |
Завдання 683
Запиши формулу функції, якщо:
а) значення функції протилежні подвоєним значенням аргументу; y = –2x
б) значення функції в 5 разів більші від значень аргументу. y = 5x
Завдання 684
Функцію задано формулою у = 2x + 5. Знайди значення функції, якщо x дорівнює: 1; 0; –3; 7; 1000.
Якщо х = 1, тоді у = 2 • 1 + 5 = 7
Якщо х = 0, тоді у = 2 • 0 + 5 = 5
Якщо х = –3, тоді у = 2 • (–3) + 5 = –1
Якщо х = 7, тоді у = 2 • 7 + 5 = 19
Якщо х = 1000, тоді у = 2 • 1000 + 5 = 2005
Завдання 685
Знайди значення функції, заданої формулою:
а) у = 8x – 5, яке відповідає значенню аргументу, що дорівнює –2; 0; 1,5; 12; 25;
Якщо х = –2, тоді у = 8 • (–2) – 5 = –21
Якщо х = 0, тоді у = 8 • 0 – 5 = –5
Якщо х = 1,5, тоді у = 8 • 1,5 – 5 = 7
Якщо х = 12, тоді у = 8 • 12 – 5 = 91
Якщо х = 25, тоді у = 8 • 25 – 5 = 195
б) у = –x/2 + 1, яке відповідає значенню аргументу, що дорівнює –8; –1; 0; 1; 20.
Якщо х = –8, тоді у = –(–8/2) + 1 = 4 + 1 = 5
Якщо х = –1, тоді у = –(–1/2) + 1 = 0,5 + 1 = 1,5
Якщо х = 0, тоді у = –(–0/2) + 1 = 0 + 1 = 1
Якщо х = 1, тоді у = –(1/2) + 1 = –0,5 + 1 = 0,5
Якщо х = 20, тоді у = –(20/2) + 1 = –10 + 1 = –9
Завдання 686
Функцію задано формулою у = 2/3x. При якому значенні аргументу значення функції дорівнює 20?
2/3 x = 20
x = 20 : 2/3
х = 20 • 3/2
x = 30
Завдання 687
Знайди значення аргументу, при якому:
а) значення функції у = 3x + 2 дорівнює 8; 2;
Якщо у = 8, тоді 8 = 3х + 2, звідси 3х = 6, х = 2
Якщо у = 2, тоді 2 = 3х + 2, звідси 3х = 0, х= 0
б) значення функції у = 4/(x – 3) дорівнює –2; 2.
Якщо у = –2, то –2 = 4/(х – 3), звідси х – 3 = –2, х = 1
Якщо у = 2, то 2 = 4/(х – 3), звідси x – 3 = 2, х = 5
Завдання 688
Напиши формулу, яка виражає залежність кута α при основі рівнобедреного трикутника від кута β при його вершині. Чи задає ця формула функцію? Яка її область визначення?
α = (180 – β)/2
Область визначення: всі числа від 0 до 180 (0 < β < 180)
Завдання 689
Швидкість автомобіля — 70 км/год. Вирази формулою залежність шляху s, пройденого цим автомобілем, від часу t. Заповни таблицю.
s = 70t
|
t, год |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
8 |
10 |
|
s, км |
70 |
140 |
210 |
280 |
350 |
4200 |
490 |
560 |
630 |
700 |
Завдання 690
Турист перебуває на відстані 5 км від міста і наближається до нього зі швидкістю 4 км/год. На якій відстані від міста буде турист через 10; 20; 30 хв? Чи є ця відстань функцією від часу? Задай її формулою. Яка її область визначення?
S = 5 – 4t
а) якщо t = 10 хв = 1/6 год, тоді 5 – 4 • 1/6 = 5 – 2/3 = 4 1/3 (км);
б) якщо t = 20 хв = 1/3 год, тоді 5 – 4 • 1/3 = 5 – 1 1/3 = 3 2/3 (км);
в) якщо t = 30 хв = 1/2 год, тоді 5 – 4 • 1/2 = 5 – 2 = 3 (км);
Область визначення: всі числа від 0 до 1,25: 0 < t < 1,25.
Завдання 691
На складі було 600 т вугілля. Щодня зі складу вивозили по 40 т вугілля. Вирази формулою залежність кількості вугілля m на складі від часу t. Чи є ця залежність функцією?
m = 600 + 40t Ця залежність є функцією.
Завдання 692
В одному дюймі — 2,54 см. Вирази формулами відповідності, які дають змогу переводити довжини в дюймах у сантиметри і в сантиметрах — у дюйми. Склади відповідні таблиці.
y = 2,54x
|
x, д |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
y, см |
2,54 |
5,08 |
7,62 |
10,16 |
12,7 |
15,24 |
17,78 |
20,32 |
22,86 |
25,4 |
x = y/2,54
|
y, cм |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
x, д |
0,39 |
0,79 |
1,18 |
1,57 |
1,97 |
2,36 |
2,76 |
3,15 |
3,54 |
3,94 |
Завдання 693
На багажних полицях літака містяться такі надписи. Виразіть формулами відповідності, які дають змогу переводити масу в кілограмах у фунти і масу у фунтах — у кілограми. Використовуйте числа, округлені до сотих. у = 0,45х і х = у/0,45
Завдання 694
Довжина кола l = 2πr, де r — його радіус. Вирази r через l. r = l : 2π
Завдання 695
З формули I = U/R вирази:
|
а) U; U = I • R |
б) R. R = U/I |
Завдання 696
Периметр квадрата P = 4a, де а довжина його сторони. Вирази a через P. a = P/4
Завдання 697
Знайди область визначення функції.
а) у = 3/4x; Множина дійсних чисел
б) у = 3/(4x); Множина дійсних чисел, крім х = 0
в) y = 3/(4 + x); Множина дійсних чисел, крім х = –4
г) y = 1/(x(x – 3)); Множини дійсних чисел, крім х = 0 і х = 3
ґ) y = x². Множина дійсних чисел
Завдання 698
Знайди область визначення функції, заданої формулою.
а) y = x(x + 5); Множина дійсних чисел
б) y = (x² + 6)(x + 8); Множина дійсних чисел, крім x = –5
в) у = 16/(x + 5); Множина дійсних чисел, крім x = 1/8
г) y = 10/(8x – 1); Множина дійсних чисел, крім x = 1/8
ґ) у = x/(x² – 36); Множина дійсних чисел, крім x = 6 і x = –6
д) у = 2x/(1 – 25x²). Множина дійсних чисел, крім x = 1/5 і x = –1/5
Завдання 699
Із квадрата, сторона якого дорівнює 10 см, вирізали круг радіуса x см (мал. 16.8). Як залежить площа утвореної фігури від x? Знайди область визначення цієї функції.
S = 100 – πx². Область визначення — множина дійсних чисел від 0 до 50: 0 < х < 50
Завдання 700
Запишіть формулу, за допомогою якої знаходять площі зафарбованих фігур, зображених на малюнку 16.9, а, б. Знайдіть область визначення одержаних функцій.
a) S = 70 – πx². Область визначення — множина дійсних чисел від 0 до 3,5: 0 < х < 3,5
б) S = 64π – πx². Область визначення — множина дійсних чисел від 0 до 8: 0 < х < 8
Завдання 701
Склади таблицю значень функції для цілих значень аргументу x, якщо –3 ≤ x ≤ 3:
а) y = { 2x + 5, якщо x ≤ 0,
–2x + 5, якщо x > 0
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
–1 |
1 |
3 |
5 |
3 |
1 |
–1 |
б) y = {x² + 3, якщо x ≤ 0,
x/2 + 3 якщо x > 0
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
12 |
7 |
4 |
3 |
3,5 |
4 |
4,5 |
Завдання 702
З’ясуй числові дані, які характеризують народжуваність в Україні за роки існування незалежної України. Запиши дані в таблицю. Чи є така відповідність функцією? Побудуй її графік за допомогою «Майстра діаграм». Коли народжуваність була найвищою, а коли — найнижчою?
ЦІКАВІ ЗАДАЧІ
Завдання 703
На дверях будинку встановлено домофон із цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Для кожної квартири надається кодовий ключ із двох будь–яких цифр. Скільки кодових ключів є вільними, якщо в будинку 96 квартир?
Розв'язання
1) 10 • 10 = 100 – кількість варіантів кодового ключа;
2) 100 – 96 = 4 – кількість кодових ключів, що є вільними.
Відповідь: 4 ключі.
Завдання 704
Знайди останню цифру значення виразу.
а) 7777 – 3333 + 2222;
б) 1422003 – 2003142;
в) 248 • 157326 + 842 • 326157.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 705
Велосипедист їде з одного села в інше зі швидкістю 10 км/год. Якби він їхав зі швидкістю 12 км/год, то приїхав би на годину раніше. Яка відстань між селами?
Розв'язання
Нехай відстань між селами x км, тоді зі швидкістю 10 км/год їхав x/10 год, а зі швидкістю 12 км/год — x/12 год. Складаємо рівняння:
x/10 – x/12 = 1 | • 60
6x – 5x = 60
x = 60 (км) – відстань між селами.
Відповідь: 60 км.
Завдання 706
Познач на координатній площині точки A(5;2), B(3;2), C(0;2), M(–1;2), H(–3;2), P(2;2). Чи всі вони лежать на одній прямій? Так
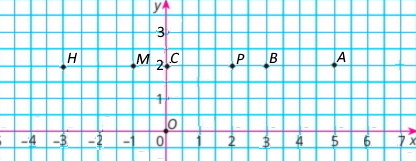
Які координати мають точки, що є серединами відрізків AB, AC, AM, AH і AP?
|
Середина відрізка |
AB |
AC |
AM |
AH |
AP |
|
Координати |
(4;2) |
(2,5;2) |
(2;2) | (1;2) | (3,5;2) |
Завдання 707 Рівняння
|
а) 4(x – 3) + 2(5 – x) = 8 4x – 12 + 10 – 2x = 8 2x = 10 x = 5 |
б) 7(5 – y) + 8(у – 3) = 18 35 – 7y + 8y – 24 = 18 y = 7 |