Завдання 786
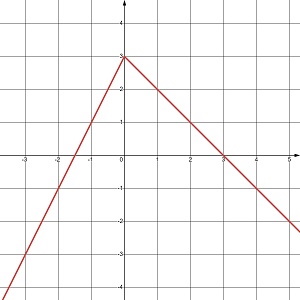
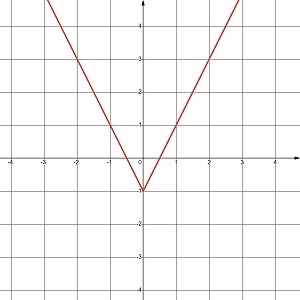
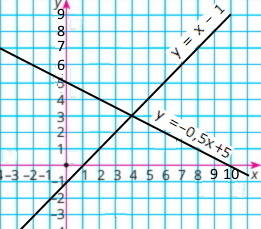
За якої умови графіки функцій у = kx – 1 і у = px + 5 перетинаються в точці P(4;3)? Знайди значення k та р. Побудуй в одній системі координат графіки цих функцій.
Точка P(4;3) лежить на прямих, тому:
3 = 4k – 1 і 3 = 4p + 5
4k = 4 і 4p = –2
k = 1 i p = –0,5
Графіки перетинаються при k = 1 і p = –0,5.
Функції мають вигляд: у = x – 1 і у = –0,5x + 5.
Завдання 787
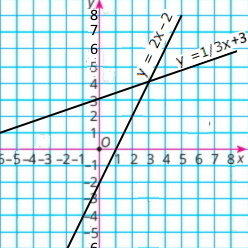
За якої умови графіки функцій у = ax + 3 і у = cx – 2 перетинаються в точці А(3; 4)? Знайди значення а та с. Побудуй в одній системі координат графіки цих функцій.
Точка P(3;4) лежить на прямих, тому:
4 = 3a + 3 і 4 = 3c – 2
3a = 1 і 3c = 6
a = 1/3 і c = 2
Графіки перетинаються при а = 1/3 і с = 2.
Функції мають вигляд: у = 1/3 x + 3 і у = 2x – 2
Завдання 788
Задай формулою функцію виду y = kx + p, якщо її графік проходить через точки:
|
а) A(0;1) і B(2;2) |
б) K(1;–1) і P(0;5) |
|
Точка А(0,1) лежить на прямій: 1 = 0 • k + р р = 1 y = kx + 1 Точка В(2,2) лежить на прямій: 2 = k • 2 + 1 2k = 1 k = 0,5 Формула функції: y = 0,5x + 1 |
Точка Р(0,5) лежить на прямій: 5 = 0 • k + p p = 5 y = kx + 5 Точка К(1,–1) лежить на прямій: –1 = k • 1 + 5 k = –1 – 5 k = –6 Формула функції: y = –6x + 5 |
Завдання 789
Задай формулою функцію виду y = kx + p, якщо її графік проходить через точки:
|
а) М(0;3) і С(–4;1) |
б) K(–3;1) і Т(0;–2) |
|
Точка М(0,3) лежить на прямій: 3 = 0 • k + p p = 3 y = kx + 3 Точка С(–4,1) лежить на прямій: 1 = –4k + 3 4k = 2 k = 0,5 Формула функції: y = 0,5x + 3 |
Точка Т(0;–2) лежить на прямій: –2 = 0 • k + p p = –2 y = kx – 2 Точка К(–3,1) лежить на прямій: 1 = –3k – 2 3k = –3 k = –1 Формула функції: y = –x – 2 |
Завдання 790
На малюнку 18.11 зображено графіки функцій виду y = kx (k ≠ 0). Для кожного графіка визначте знак коефіцієнта k. Складіть формули, що відповідають графікам цих функцій.
|
а) |
б) |
в) |
г) |
|
k = 3; y = 3x |
k = 0,5; y = 0,5x |
k = –1; y = –x |
k = –0,2; y = –0,2x |
Завдання 791
Напиши формули функцій, графіки яких зображено на:
|
а) малюнку 18.12 |
б) малюнку 18.13 |
||
|
a: 3 = 0k + b b = 3 0 = –2k + 3 k = 3/2 = 1,5 y = 1,5x + 3
|
b: –3 = 0k + b b = –3 0 = 2k – 3 k = 1,5 y = 1,5x – 3 |
a: –2 = 0k + b b = –2 0 = –4k – 2 k = –0,5 y = –0,5x – 2
|
b: 4 = 0k + b b = 4 0 = –4k + 4 4k = 4 k = 1 y = x + 4 |
Завдання 792
На фарбування 1 м² підлоги затрачують 180 г фарби. Виразіть формулою залежність маси m фарби від площі s підлоги, яку фарбуватимуть. Чи є ця залежність прямою пропорційністю? m = 180s — формула залежності. Так, є прямою пропорційністю.
Завдання 793
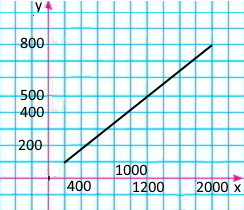
Витрати виробництва на 200 одиниць продукції становлять 100 грн, а на 2000 одиниць — 800 грн. Знайди графічно витрати на виробництво 400, 1000, 1200 одиниць продукції, вважаючи, що функція витрат — лінійна.
Якщо х = 400, то у = 200; якщо х = 1000, то у = 400; якщо х = 1200, то у = 500.
Відповідь: 200 грн, 400 грн, 500 грн.
Завдання 794
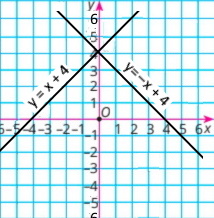
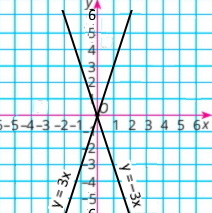
Для кожного графіка побудуй графік, симетричний даному відносно осі ординат. Задай формулою відповідну функцію.
|
а) y = x + 4 у = –х + 4 |
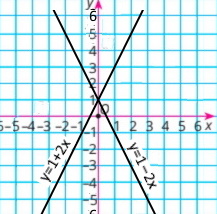
б) у = 1 – 2x у = 1 + 2х |
в) у = 3x у = –3х |
|
|
|
 |
Завдання 795
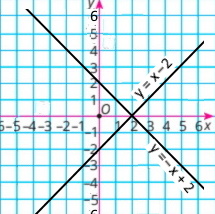
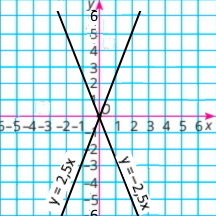
Для кожного графіка побудуй графік, симетричний даному відносно осі абсцис. Задай формулою відповідну функцію.
|
а) y = –x + 2 у = х – 2 |
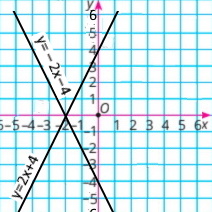
б) y = 2x + 4 у = –2х – 4 |
в) y = 2,5x у = –2,5х |
|
|
|
 |
Завдання 796
|
а) y = 2x + 3, x < 0, –x + 3, x > 0; |
б) y = –3x + 3, x < 1, x – 1, x > 1 |
|
|
|
Завдання 797
|
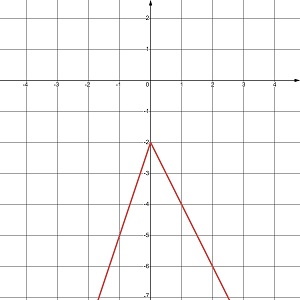
а) у = 3x – 2, x < 0, –2x – 2, x > 0 |
б) у = –2x – 2, x < –1, x + 1, x > –1. |
|
|
|
Завдання 798
|
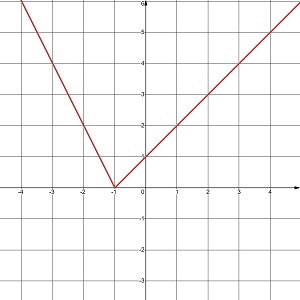
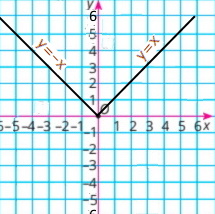
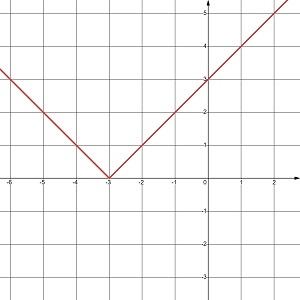
а) у = |x| |
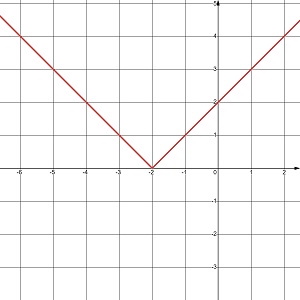
б) у = |x + 3| |
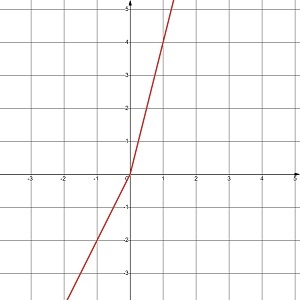
в) у = |x| + 3x |
|
|
|
|
Завдання 799
|
а) у = |x + 2| |
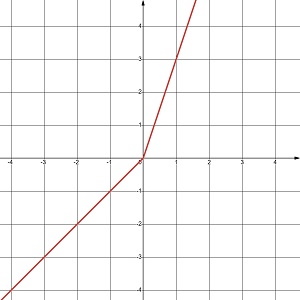
б) у = 2x + |x| |
в) 2|x| – 1 |
|
|
|
|
ЦІКАВІ ЗАДАЧІ
Завдання 800
Витрати при перевезенні вантажу двома видами транспорту обчислюються за
формулами: у1 = 100 + 30x, у2 = 150 + 20x, де x — відстань перевезень у
сотнях кілометрів, у1 і у2 — транспортні витрати при перевезенні вантажу
першим і другим видами транспорту в тисячах гривень. Визнач, на які
відстані і яким видом транспорту краще перевозити вантаж.
Знайдемо точку перетину графіків:
100 + 30х = 150 + 20х
10х = 50
х = 5
у = 100 + 30 • 5 = 100 + 150 = 250, тому (5; 250) – точка перетину прямих.
Оскільки х – відстань перевезень у сотнях кілометрів. А у1 і у2 – транспортні
витрати у сотнях гривень, то на відстані 5 • 100 = 500(км) транспортні витрати
обома видами транспорту становлять 250 • 100 = 25 000(грн).
Якщо відстань менша, ніж 5 сотень км, маємо х = 1, тому
у1 = 100 + 30 • 1 = 130 сотень грн;
у2 = 150 + 20 • 1 = 170 сотень грн.
130 < 170
у1 < у2
Отже, вигідніше користуватися першим видом транспорту.
Якщо відстань більша, ніж 5 сотень км, маємо х = 6, тому
у1 = 100 + 30 • 6 = 280 сотень грн;
у2 = 150 + 20 • 6 = 270 сотень грн.
280 > 270
у1 > у2
Отже, вигідніше користуватися другим видом транспорту.
Завдання 801
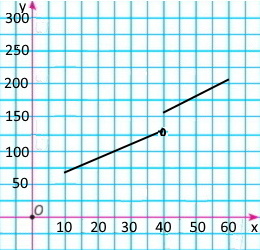
Фірма платить продавчині за x одиниць проданого товару (2x + 50) грн, якщо продано товару менш ніж 40 одиниць, і доплачує їй 20% комісійних, якщо товару продано 40 одиниць і більше. Опиши залежність між кількістю проданого товару та заробітною платою продавчині і побудуй графік цієї залежності.
а) Якщо продано менш, ніж 40 одиниць: у = 2x + 50, x < 40, а
якщо продано 40 одиниць і більше: у = (2x + 50)1,2 = 2,4х + 60, x ≥ 40
|
х |
10 |
20 |
30 |
40 |
50 |
60 |
|
у |
70 |
90 |
110 |
156 |
180 | 204 |
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 802 Розкладна множники многочлена
а) ab + bc + a + c = b(a + c) + (a + c) = (b + 1)(a + c);
б) 2x – yx + 2у – у² = x(2 – y) + y(2 – y) = (x + y)(2 – y);
в) 3 – 6a + z – 2az = 3(1 – 2a) + z(1 – 2a) = (3 + z)(1 – 2a);
г) 10ax – 5bx + 2ау – bу = 5x(2a – b) + y(2a – b) = (5x + y)(2a – b).
Завдання 803 Рівняння
|
а) (2x + 3)² = 4x² + 3 4x² + 12x + 9 = 4x² + 3 12x = –6 x = –1/2 |
б) (5 – 3у)² – 9у² = 55 25 – 30y + 9y² – 9у² = 55 –30y = 30 y = –1 |
|
в) (4z + 2)²= 2(8z² + 13) 16z² + 16z + 4 = 16z² + 26 16z = 22 z = 22/16 = 1 6/16 |
г) (4 – 5x)² = (3 + 5x)² 16 – 40x + 25x² = 9 + 30x + 25x² 70x = 7 x = 1/10 |
Завдання 804
Мотоцикліст проїжджає відстань від Жашкова до Умані за 1 год, а велосипедист від Умані до Жашкова — за 5 год. Через скільки годин вони зустрінуться, якщо виїдуть одночасно?
Розв'язання
Нехай відстань між містами х км, тоді швидкість мотоцикліста х/1 км/год, а велосипедиста — х/5 км/год.
1) х/1 + х/5 = 6/5 х (км/год) – швидкість зближення;
2) х : 6/5 х = 5/6 (год) = 50 (хв)– час, коли вони зустрінуться.
Відповідь: 50 хв.