ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ
ВАРІАНТ І
Завдання 1
Знайди значення функції у = 2х² – 3, якщо:
а) х = 2; 2 • 2² – 3 = 5, отже, у = 5
б) х = –3. 2 • (–3)² – 3 = 15, отже, у = 15
Завдання 2
Через яку з точок А(–1;–2); В(–2;19) проходить графік функції у = 5 – 7х?
5 – 7 • (–1) = 12, отже, графік функції не проходить через точку А(–1;–2);
5 – 7 • (–2) = 19, отже, графік функції проходить через точку В(–2;19).
Завдання 3
Побудуй графік функції у = 2х – 1.
|
х |
0 |
1 |
|
у |
–1 |
1 |
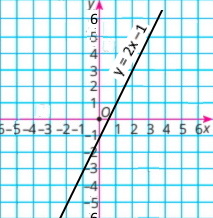
Користуючись ним, знайди:
а) якщо x = 2, тоді y = 3; якщо x = –1, тоді y = –3
b) y = –5, якщр x = –2; y = 7, якщр x = 4
Завдання 4 Область визначення функції
а) у = x² – 3x + 2;
Область визначення функції – всі дійсні числа;
б) у = 2/(х + 3).
x + 3 ≠ 0; x ≠ –3, отже область визначення функції – всі дійсні числа, окрім x = –3.
ВАРІАНТ II
Завдання 1
Знайди значення функції у = 3х² + 7, якщо:
а) х = 3; 3 • 3² + 7 = 34
б) х = –2. 3 • (–2)² + 7 = 19
Завдання 2
Через яку з точок А(3;37); В(–2;28) проходить графік функції у = –2 + 13х?
–2 + 13 • 3 = 37 – графік функції проходить через точку А(3;37);
–2 + 13 • (–2) = –28 – графік функції не проходить через точку В(–2;28).
Завдання 3
Побудуй графік функції у = 5 – 3х.
|
х |
0 |
2 |
|
у |
5 |
–1 |
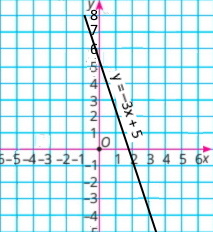
Користуючись ним, знайди:
а) Якщо x = 3, тоді y = –4; якщо x = –1, тоді y = 8
b) y = 2, якщо x = 1; y = –1, якщо x = 2
Завдання 4
Знайди область визначення функції.
а) у = x3 – x + 3;
Область визначення функції – всі дійсні числа;
б) у = 3/(x – 2). x – 2 ≠ 0; x ≠ 2, отже область визначення функції – всі дійсні числа, окрім x = 2.
ГОТУЄМОСЯ ДО ТЕМАТИЧНОГО ОЦІНЮВАННЯ
Тестові завдання № 5
Завдання 1
Через яку з точок проходить графік функції у = 3x + 2?
3 • 4 + 2 = 14, графік функції проходить через точку D(4; 14), тому Г D(4;14)
Завдання 2
Графік функції y = 2x + 10 перетинає вісь абсцис у точці з координатами:
Якщо у = 0, тоді 2 • 0 + 10 = 10, тому В (0;10)
Завдання 3
Графік функції y = –x + 5 перетинає вісь ординат у точці з координатами:
Якщо у = 0, тоді 0 = –x + 5; x = 5, отже, в точці (5;0), тому В (5;0)
Завдання 4 Лінійна функція
А y = x/2 + 3
Завдання 5 Функція прямої пропорційності
Г y = 3x
Завдання 6
Задай формулою функцію, значення якої на 4 більші за відповідні значення аргументу.
Оскільки х – аргумент функції, тоді у = х + 4, тому Б у = x + 4
Завдання 7
При якому значенні k графік функції у = kx + 7 проходить через точку C(2;–1)?
–1 = 2k + 7; 2k = –8; k = –4, тому А –4
Завдання 8
Які значення x не входять до області визначення функції y = 3/(x(x – 2))?
x(x – 2) ≠ 0; x ≠ 0 або x – 2 ≠ 0; x ≠ 0 або x ≠ 2, тому В 0 і 2.
Завдання 9
Який із графіків функцій не перетинає вісь абсцис? Г y = –3
Завдання 10
Якщо x = –0,2, то у = –1/(4x + 1) = –1/(4 • (–0,2) + 1) = –1/0,2 = –5, тому В –5
ТИПОВІ ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ № 5
Завдання 1
Не виконуючи побудови графіка функції у = 7x – 3, укажи, через яку з точок проходить графік функції.
7 • 0 – 3 = –3 Графік функції проходить через точку D(0;–3), тому Г D(0;–3).
Завдання 2
Графік функції у = 8х – 24 перетинає вісь абсцис у точці з координатами:
Якщо х = 0, то 8 • 0 – 24 = –24, точка А (0;–24) лежить на абсцисі, тому Г (0;–24).
Завдання 3
Яка з даних функцій набуває лише додатних значень? В у = 3
Завдання 4
Установи відповідність між функціями, заданими умовами (1–3), та значеннями цих функцій (А–Д) за умови, що х = –1,2.
|
1 у = 2х – 0,4 2 у = –5х + 3 3 у = 0,2х – 0,24 |
А 0 Б 2 В 9 Г –2,8 Д –0,48 |
1 у = 2х – 0,4; 2 • (–1,2) – 0,4 = –2,8
2 у = –5х + 3; –5 • (–1,2) + 3 = 9
3 у = 0,2х – 0,24. 0,2 • (–1,2) – 0,24 = –0,48
Відповідь: 1 – Г; 2 – В; 3 – Д.
Завдання 5
Побудуй графік функції y = –2x + 4.
|
х |
0 |
2 |
|
у |
5 |
–1 |
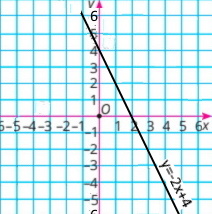
Користуючись графіком, знайди:
а) якщо x = –1, то y = 6; якщо x = 0, то y = 4; якщо x = 3, то y = –2
b) y = –6, якщо x = 16; y = 0, якщо x = 2; y = 2, якщо x = 1
в) координати точок перетину графіказ осями координат; (0;2), (4;0)
г) функція набуває додатних значень, якщо x < 2
Завдання 6
Знайди область визначення функції у = 6/(x² – 5x).
x² – 5x ≠ 0; x(x – 5) ≠ 0; x ≠ 0 або x – 5 ≠ 0; отже, x ≠ 0 або x ≠ 5.
Завдання 7
Побудуй в одній системі координат графіки функцій у = –3х + 5 і у = х + 1.
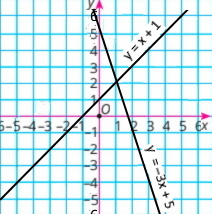
Графіки перетинаються в точці з координатами (1;2).
Завдання 8
Задай формулою лінійну функцію, графік якої проходить через початок координат і точку A(–4;–6).
Точка A(–4;–6) лежить на прямій y = kx + l, тому –6 = –4k + l; k = 2, тоді l = –6 + 8 = 2;
формула такої лінійної функції y = 2x + 2.
Додаткове завдання
Завдання 9
Одна сторона прямокутника дорівнює x см, а інша — на 2 см більша. Вирази формулою залежність периметра Р прямокутника від x. Побудуй графік утвореної функції. Знайди її область визначення і множину значень. Користуючись графіком, знайди периметр прямокутника для х = 1 см.
Функція периметра: P(x) = 4x + 4.
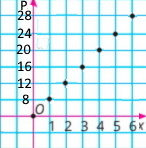
Область визначення: множина натуральних чисел.
Множиною значень є натуральні числа.
P(1) = 4 • 1 + 4 = 8 (см) – периметр прямокутника.