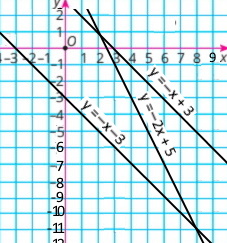
Завдання 1045 Система двох лінійних рівнянь з двома змінними
|
А {x – у = 2 x² – у = 3 |
Б {x² + у² = 4 x – у = 3 |
В {x – 2у = 4 2x + 3у = 1 |
Г {ху = 6 x + 2у = 2 |
Завдання 1046
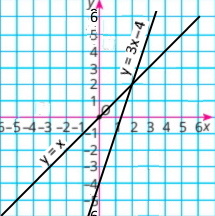
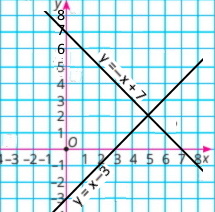
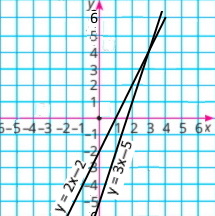
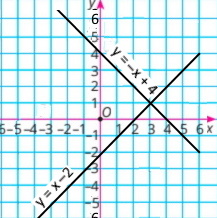
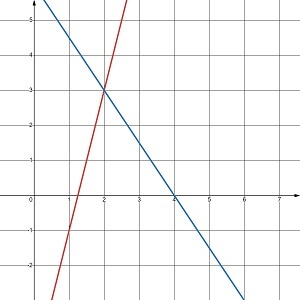
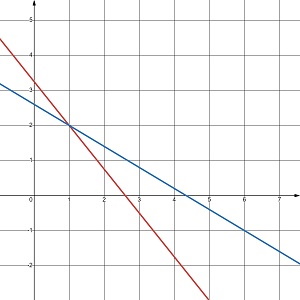
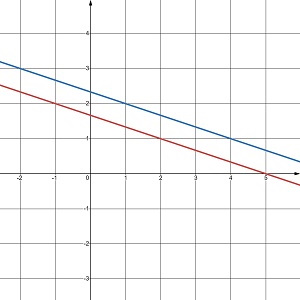
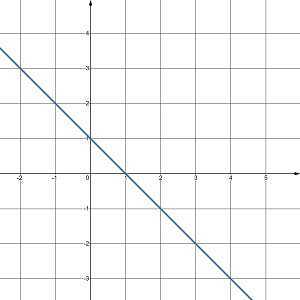
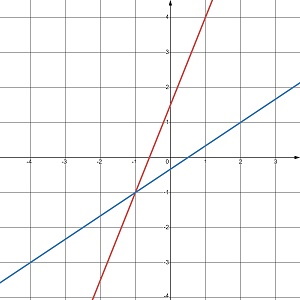
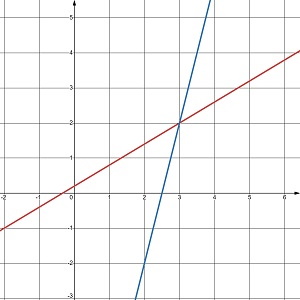
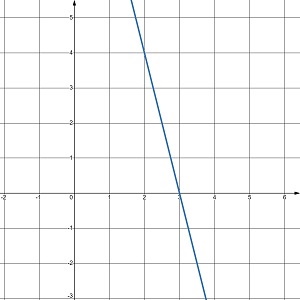
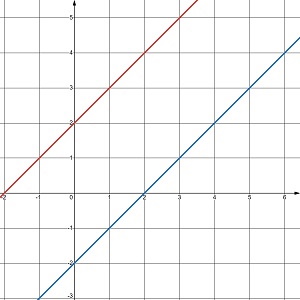
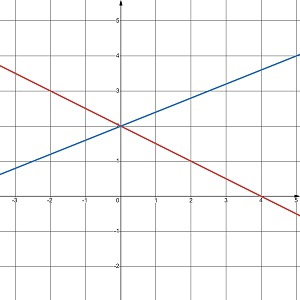
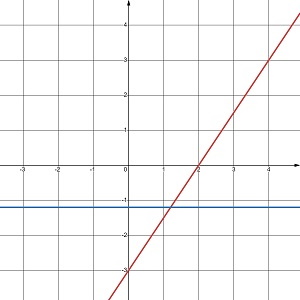
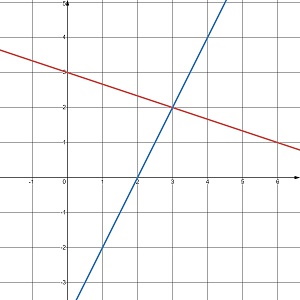
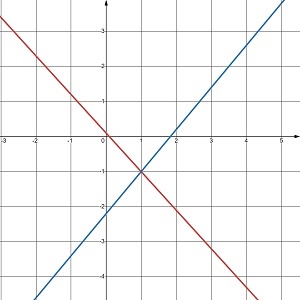
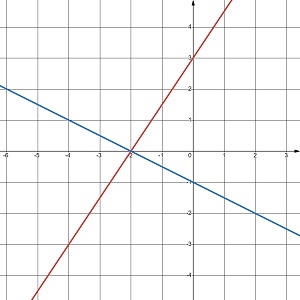
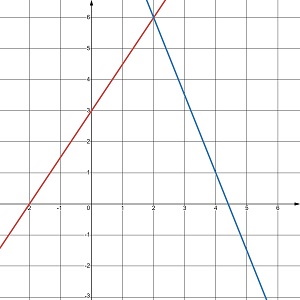
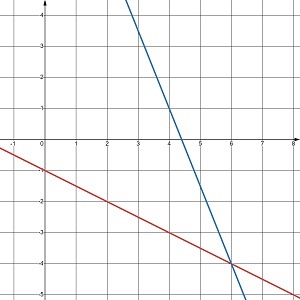
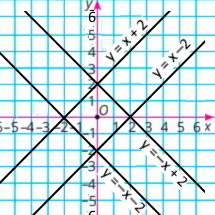
Скільки розв’язків має система рівнянь, графіки яких зображено на малюнку 24.5?
|
а. один розв’язок |
б. жодного розв’язку |
в. один розв’язок |
Завдання 1047
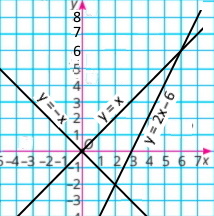
Яка з пар чисел є розв’язком системи рівнянь?
|
А (0;4) |
Б (–1;3) |
В (–7;–3) |
Г (1;4) |
|
{x – у = –4 x – 2у = –7 {0 – 4 = –4 0 – 2 • 5 = –8 |
{x – у = –4 x – 2у = –7 {–1 – 3 = –4 –1 – 2 • 3 = –7 Розв'язок |
{x – у = –4 x – 2у = –7 {–7 – (–3) = –4 –7 – 2 • (–3)= –1
|
{x – у = –4 x – 2у = –7 {1 – 4 = –3 1 – 2 • 4 = –7 |
Завдання 1048
Скільки розв’язків має система рівнянь?
|
а) {3x + 4у = 2 9x + 12у = 6 |:3 {3x + 4у = 2 3x + 4у = 2 Безліч розв’язків |
б) {2x – у = 5 4x + 2у = 10 |:2 {2x – y = 5 2x + y = 5 Один розв’язок |
в) {x – 5у = 4 –2x + 10у = 8 |:(–2) {x – 5у = 4 x – 5у = –4 Жодного розв’язку |
Завдання 1049
Чи є пара чисел (2;–1) розв’язком системи рівнянь?
|
а) {x + у = 1 x – 2y = 6 {2 + (–1) = 1 2 – 2 • (–1) = 4 Не є розв'язком |
б) {x + y = 1 4x – 3у = 11 {2 + (–1) = 1 4 • 2 – 3 • (–1) = 11 Є розв'язком |
в) {x – у = 3 2x + у = 3 {2 – (–1) = 3 2 • 2 + (–1) = 3 Є розв’язком |
Завдання 1050
Чи є пара чисел (–1; 3) розв’язком системи рівнянь?
|
а) {x + у = 2 3x – у = –6 {–1 + 3 = 2 3 • (–1) – 3 =–6 Є розв’язком |
б) {3x + у = 0 x + 2у = 5 {3 • (–1) + 3 = –3 + 3=0 –1 + 2 • 3 = –1 + 6 =5 Є розв’язком |
в) {3x – 2у = –9 3x + 2у = –3 {3 • (–1) – 2 • 3=–9 3 • (–1) + 2 • 3=3 Не є розв’язком |
Завдання 1051
Склади систему рівнянь, що має розв’язок:
|
а) (3;4) |
б) (2;–5) |
в) (0;3) |
г) (–2;0) |
|
{x – y = –1 |
{x + 2y = –8 |
{x + y = 3 |
{x – y = –2 |
Завдання 1052
Склади систему рівнянь, що має розв’язок:
|
а) (2;1) |
б) (–3;2) |
в) (5;0) |
г) (0;–4) |
|
{x + y = 3 |
{x – y = –5 |
{x + y = 5 |
{x – y = 4 |
Завдання 1053
|
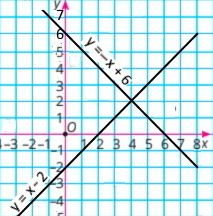
а) {x + у = 6 x – у = 2 |
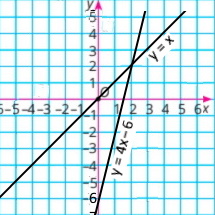
б) {x – у = 0 4x – у = 6 |
||||||||||||||||||||||||||
|
у = –х + 6 |
у = х – 2 |
у = х |
у = 4х – 6 | ||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
Відповідь: (4;2) |
Відповідь: (2;2) |
||||||||||||||||||||||||||
|
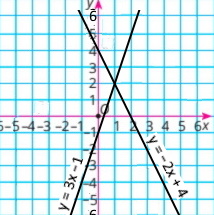
в) {2x + у = 4 3x – у = 1 |
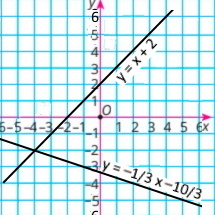
г) {x – у = –2 x + 3у = –10 |
||||||||||||||||||||||||||
|
у = –2х + 4 |
у = 3х – 1 |
у = х + 2 |
у = –1/3 х – 10/3 | ||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
Відповідь: (1;2) |
Відповідь: (–4;–2) |
||||||||||||||||||||||||||
Завдання 1054
|
а) {x – y = 0 3x – y = 4 |
б) {x + y = 7 x – y = 3 |
||||||||||||||||||||||||||
|
у = х |
у = 3х – 4 |
у = –х + 7 |
у = х – 3 | ||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
Відповідь: (2;2) |
Відповідь: (5;2) |
||||||||||||||||||||||||||
|
в) {2x – y = 2 3x – y = 5 |
г) {x + y = 4 x – y = 2 |
||||||||||||||||||||||||||
|
у = 2х – 2 |
у = 3х – 5 |
у = –х + 4 |
у = х – 2 | ||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
Відповідь: (3;4) |
Відповідь: (3;1) |
||||||||||||||||||||||||||
Завдання 1055
|
а) {4x – у = 5 3x + 2у = 12 |
б) {5x + 4у = 13 3x + 5у = 13 |
||
|
Відповідь: (2;3) |
Відповідь: (1;2) |
||
|
в) {x + 3у = 5 3x + 9у = 21 |
г) {x + у = 1 –2x – 2у = –2 |
||
|
Відповідь: не існує розв'язків |
Відповідь: безліч розв'язків |
Завдання 1056
|
а) {5x – 2у = –3 2x – 3у = 1 |
б) {–3x + 5у = 1 4x – у = 10 |
||
|
Відповідь: (–1;–1) |
Відповідь: (3;2) |
Завдання 1057
|
а) {2x + 1/2у = 6 4x + у = 12 |
б) {x – у = –2 3x – 3у = 6 |
||
|
Відповідь: безліч розв'язків |
Відповідь: не існує розв'язків |
Завдання 1058
Діана почала будувати блок–схему для того, щоб визначити, скільки розв’язків має довільна система рівнянь ax + by = c, kx + ty = p але не завершила. Допоможи їй.
|
один розв’язок |
жодного розв’язку |
безліч розв’язків |
Завдання 1059
Скільки розв’язків має система рівнянь?
|
а) {x + 3у = 5 8x + 9у = 10 1/8 ≠ 3/9 Один розв’язок |
б) {x – 4у = 1 2x – 8у = 3 1/2 = 4/8 ≠ 1/3 Жодного розв’язку |
Завдання 1060
How many solutions does the system of equations have?
|
а) {x + у = 8 2x – у = 13 1/2 ≠ 1/(–1) Один розв’язок |
b) {–x + 5у = 7 2x – 10у = –14 (–1)/2 = 5/(–10) = 7/(–14) Безліч розв’язків |
Завдання 1061
Не будуючи графіків, доведи, що система рівнянь не має розв’язків.
|
а) {8x + 2у = 15 8x + 2у = 35 8/8 = 2/2 ≠ 15/35 Жодного розв’язку, бо прямі паралельні |
б) {3x – у = 8 3x – у = 16 3/3 = (–1)/(–1) ≠ 8/16 Жодного розв’язку, бо прямі паралельні |
Завдання 1062
Не будуючи графіків, доведи, що система має безліч розв’язків. Знайди три будь–які її розв’язки.
{6x + 10у = 36
3x + 5у = 18
6/3 = 10/5 = 36/18 – безліч розв’язків, бо графіки збігаються.
Будь–які три розв’язки даної системи рівнянь:
Якщо х = 1, то 6 + 10у = 36; 10у = 30; у = 3.
Якщо х = 6, то 36 + 10у = 36; 10у = 0; у = 0.
Якщо х = 11, то 66 + 10у = 36; 10у = -30; у = -3.
Відповідь: (1;3), (6;0), (11;-3).
Завдання 1063
Розв’яжи графічно систему рівнянь
|
а) {0,5x + у = 2 –0,4x + у = 2 |
б) {1,5x – у = 3 0,3x + у = –1,2 |
||
|
Відповідь: (0;2) |
Відповідь: (1;–1,5) |
Завдання 1064
|
а) {0,2x + 0,6у = 1,8 x – 0,5у = 2 |
б) {1,1x + у = 0,1 1,2x – у = 2,2 |
||
|
Відповідь: (3;2) |
Відповідь: (–1;–1) |
Завдання 1065
Із даних рівнянь утворіть та розв’яжіть усі можливі системи.
|
а) 3x – 2y = –6; |
б) x + 2y = –2; |
в) 5x + 2y = 22. |
|
{3x – 2у = –6 x + 2у = –2 |
{3x – 2у = –6 5x + 2у = 22 |
{x + 2у = –2 5x + 2у = 22 |
|
Відповідь: (–2;0) |
Відповідь: (2;6) |
Відповідь: (6;–4) |
Завдання 1066
Розв’яжи систему рівнянь графічно та перевір, чи є одержаний розв’язок точним.
{5x – 4у = 1
12x + 22у = 33
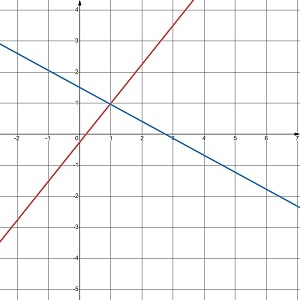
Одержаний розв’язок (1;1) не є точним.
5 • 1 – 4 • 1 = 1; 12 • 1 + 22 • 1 = 34, 34 ≠ 33
Чи задовольняє систему рівнянь пара чисел (77/79; 153/158)? Так, задовільняє.
5 • 77/79 – 4 • 153/158 = 385/79 – 612/158 = 770/158 – 612/158 = 158/158 = 1
12 • 77/79 + 22 • 153/158 = 924/79 + 3366/158 = 1848/158 + 3366/158 = 5214/158 = 33.
Завдання 1067
Розв’яжи систему рівнянь графічно та перевір, чи є одержаний розв’язок точним.
{3x + 2у = 7
11x – 20у = 55
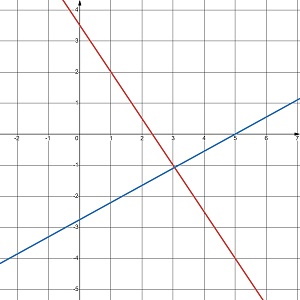
Одержаний розв’язок (3;–1) не є точним.
3 • 3 + 2 • (–1) = 9 – 2 = 7; 11 • 3 – 20 • (–1) = 33 + 20 = 53, 53 ≠ 55
Чи задовольняє систему рівнянь пара чисел (3 2/41;–1 3/41)? Так, задовільняє.
3 • 3 2/41 + 2 • (–1 3/41) = 3 • 125/41 – 2 • 44/41 = 375/41 – 88/41 = 287/41 = 7
11 • 3 2/41 – 20 • (–1 3/41) = 11 • 125/41 + 20 • 44/41 = 1375/41 + 880/41 = 2255/41 = 55
Завдання 1068
Склади рівняння з двома змінними, яке в системі з даним:
|
1) має безліч розв’язків а1/а2 = b1/b2 = c1/c2 |
2) не має жодного розв’язку a1/a2 = b1/b2 ≠ с1/с2 |
3) має один розв’язок a1/a2 ≠ b1/b2 |
|
а) {3x – у = 5 6x – 2у = 10 б) {3x – 2у = 2 6x – 4у = 4 |
а) {3x – у = 5 3x – у = 6 б) {3x – 2у = 2 3x – 2у = 7 |
а) {3x – у = 5 3x – 2у = 5 б) {3x – 2у = 2 3x – у = 2 |
Завдання 1069
|
1) має безліч розв’язків а1/а2 = b1/b2 = c1/c2 |
2) не має жодного розв’язку a1/a2 = b1/b2 ≠ с1/с2 |
3) має один розв’язок a1/a2 ≠ b1/b2 |
|
а) {5x + 4у = 1 10x + 8у = 2 б) {x + у = –4 2x + 2у = –8 |
а) {5x + 4у = 1 5x + 4у = 3 б) {x + у = –4 x + у = –1 |
а) {5x + 4у = 1 5x + у = 1 б) {x + у = –4 x + 3у = –4 |
Завдання 1070
При якому значенні а система рівнянь:
|
а) {3x – у = 3 |:3 x – ау = 1 {x – 1/3у = 1 х – ау = 1 1) має один розв’язок, коли а ≠ 1/3 2) має безліч розв’язків, коли а = 1/3 |
б) {7x + 2у = 11 |•2 ax + 4у = 22 {14x + 4у = 22 ax + 4у = 22 1) має один розв’язок, коли а ≠ 14 2) має безліч розв’язків, коли а = 14 |
Завдання 1071
При якому значенні b система рівнянь:
|
а) {bx + 2у = 7 3x – у = 5 |•(–2) {bx + 2у = 7 –6x + 2у = –10 1) не має розв’язку, коли b = –6 2) має один розв’язок, коли b ≠ –6 |
б) {4x + 8у = 5 2x + bу = –1 |•2 {4x + 8у = 5 4x + 2bу = –2 1) не має розв’язку, коли b = 4 2) має один розв’язок, коли b ≠ 4 |
Завдання 1072
Чи має розв’язок система рівнянь?
|
а) {x – y = 1 x + y = 3 2x = 6 З третього рівняння: 2х = 6, х = 3 Підставляємо в перше рівняння: 3 - у = 1, у = 2 Підставляємо х і у в друге рівняння: 3 + 2 = 5, 5 ≠ 3. Не задовільняє рівняння, тому система не має розв'язку. |
б) {3x – y = 1 x + y = 3 4y = 8 З третього рівняння: 4у = 8, у = 2. Підставляємо в друге рівняння: х + 2 = 3, х = 1 Підставляємо х і у в перше рівняння: 3 - 1 = 1. Задовільняє рівняння, тому система має розв’язок (1;2) |
|
в) {3x + y = 13 5x – 4у = –1 7x – 5у = 1 З першого рівняння: 3х + у = 13, у = 13 - 3х Підставляємо в друге рівняння: 5х - 4(13 - 3х) = -1 5х - 52 + 12х = -1 17х = 51 х = 3 Підставляємо х в перше рівняння: у = 13 - 3 • 3 = 4 Підставляємо х і у в третє рівняння: 7 • 3 - 5 • 4 = 21 - 20 = 1. Задовільняє рівняння, тому система має розв'язок (3;4). |
г) {2x + 7у = 16 3х – у = 1 x + 4у = 1 З другого рівняння: 3х - у = 1, у = 3х - 1 Підставляємо в перше рівняння: 2х + 7(3х - 1) = 16 2х + 21х - 7 = 16 23х = 23 х = 1 Підставляємо х в друге рівняння: у = 3 • 1 - 1 = 2 Підставляємо х і у в третє рівняння: 1 + 4 • 2 = 9, 9 ≠ 1. Не задовільняє рівняння, тому система не має розв'язку. |
Завдання 1073
При якому значенні k система рівнянь має розв’язок?
|
а) {3x – 2у = –1 5x – 3у = 2 2x + kу = 25 |
б) {k(x + у) + 5x = 2 9x + 11у = 7 4x – 3у = 11 |
|
{3x – 2у = –1 5x – 3у = 2 Розв'язок (7;11), тому 2x + kу = 25 2 • 7 + k • 11 = 25 14 + 11k = 25 11k = 11 k = 1
Відповідь: при k = 1 |
б) {9x + 11у = 7 4x – 3у = 11 Розв’язок (2;–1), тому k(x + у) + 5x = 2 k(2 – 1) + 5 • 2 = 2 k + 10 = 2 k = –8 Відповідь: при k = –8 |
ЦІКАВІ ЗАДАЧІ
Завдання 1074
Розв’яжи графічно систему рівнянь.
|
а) {x² – у² = 0 2x – у = 6 {(x – у)(х + у)= 0 2x – у = 6 {x – у=0 або {х + у=0 2x – у=6 2x – у=6 |
б) {x² + 2xy + у² = 9 2x + у = 5 {(x + y)² = 3² 2x + у = 5 {x + y=3 або {х + у=–3 2x + у=5 2x + у=5 |
в) {|x – у| = 2 |x + у| = 2 {x – у=2 або {x – у=2 x + у=2 x + у=–2 {x – у=–2 або {x – у=–2 x + у=2 x + у=–2 |
|
(6;6); (2;–2) |
(2;1), (8;–11) |
(2;0), (–2;0), (0;2), (0;–2) |
Завдання 1075 Числові послідовності
Допиши ще один рядок послідовності.
1 + 2 = 3
4 + 5 + 6 = 7 + 8
9 + 10 + 11 + 12 = 13 + 14 + 15
16 + 17 + 18 + 19 + 20 = 21 + 22 + 23 + 24
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 1076 Вирази
а) 3x3 – 2x² – x(3x² + 2x – 5) = 3x3 – 2x² – (3x3 + 2x² – 5x) =
= 3x3 – 2x² – 3x3 – 2x² + 5x = –4x² + 5x
Якщо x = 5, тоді –4 • 5² + 5 • 5 = –4 • 25 + 25 = –100 + 25 = –75
б) (8a² – a3)a + (a² – 8a + 5)a² = 8a3 – a4 + a4 – 8a3 + 5a² = (8a3 – 8a3) + (–a4 + a4) + 5a² =
= 5a²
Якщо a = 0,2, тоді 5 • 0,2² = 5 • 0,04 = 0,2
Завдання 1077 Множення двочленів
a) (x + 3)(x – 2) = x² – 2х + 3x – 6 = x² + x – 6
б) (a – 5)(a + 4) = a² + 4а – 5a – 20 = a² – a – 20
в) (m + n)(m – n) = m² – mn + mn – n² = m² – n²
г) (3 – z)(5 + z) = 15 + 3z – 5z – z² = 15 – 2z – z²
Завдання 1078
Щоб одержати бронзу, беруть 17 частин міді, 2 частини цинку й одну частину олова. Скільки кілограмів міді, цинку й олова слід узяти, щоб виготовити 200 кг бронзи?
Розв'язання
Нехай одна частина становить x кг. Складаємо рівняння:
17x + 2x + x = 200
20x = 200
x = 10
17 • 10 = 170 (кг) – узяли міді;
2 • 10 = 20 (кг) – узяли цинку;
1 • 10 = 10 (кг) – узяли олова.
Відповідь: 170 кг, 20 кг і 10 кг.