
Завдання 915
За графіком функції y = f (x), зображеним на рисунку 28, заповніть таблицю:
|
x |
–3 |
–2 |
0 |
2 |
6 |
7 |
|
y |
3 |
4 |
5 |
3 |
0 |
4 |
Завдання 916
За графіком функції y = f (x), зображеним на рисунку 29, заповніть таблицю:
|
x |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
f(x) |
0 |
2 |
3 |
2 |
0 |
–2 |
–3 |
–2 |
0 |
Завдання 917
За графіком функції на рисунку 30, знайдіть:
a) область визначення: –1 ≤ x < 4, область значень: 1 ≤ y < 4
б) область визначення: –1 ≤ x ≤ 3, область значень: 1 ≤ y ≤ 4
в) область визначення: –2 ≤ x < 3, область значень: 1 < y ≤ 3
г) область визначення: –3 < x < 4, область значень: y = 2
ґ) область визначення: x = 1, x = 3, область значень: y = 1, у = –2
Завдання 918
За графіком функції на рисунку 31, знайліть:
a) область визначення: –2 ≤ x < 2, область значень: –1 < y ≤ 4
б) область визначення: –2 ≤ x ≤ 2, область значень: 1 ≤ y ≤ 3
в) область визначення: –2 ≤ x < 3, область значень: 1 ≤ y < 3
г) область визначення: –3 < x < 2, область значень: y = –2
ґ) область визначення: x = –3, x = 4, область значень: y = –1, y = 3
Завдання 919
За графіком функції y =f(x) на рисунку 28 знайдіть:
1) значення аргументу, при яких у = 3; x = –3, x = 2, x = 6,5
2) значення аргументу, при яких функція дорівнює нулю; x = –5, x = 3, x = 6
3) область визначення функції; –5 ≤ x ≤ 7
4) область значень функції; –2 ≤ у ≤ 5
5) значення аргументу для від’ємних значень функції; –3 < x < 6
6) значення аргументу для додатних значень функції. –5 < x < 3; 6 < x ≤ 7
Завдання 920
За графіком функції на рисунку 32 знайдіть:
1) Якщо x = –3,5, то у = –1,5; якщо х = –1,5, то у = 3,5; якщо х = 2, то у = –1;
якщо х = 4, то у = 2;
2) у = –3, якщо х =–4; у = –1,5, якщо х = –3,5 і х = 2,5;
у = 2, якщо х = –2,5, х = –1 і х = 4;
3) якщо у = 0, то х = –3, х = 1,5 і х = 3,5;
4) область визначення: –4,5 ≤ х ≤ 5; область значень: –3,5 ≤ у ≤ 4;
5) у > 0 при –3 < х < 1,5 і 3,5 < х ≤ 5;
6) у < 0 при –4,5 ≤ х < –3 і 1,5 < x < 3,5.
Завдання 921
За графіком функції y = f(x) на рисунку 33 знайдіть:
1) область визначення функції: –6 ≤ х ≤ 6
2) область значень фукнції: –5 ≤ у ≤ 5
3) координати точок перетину графіка функції з віссю абсцис;
(–5;0), (–3;0), (3;0), (5;0)
4) координати точки перетину графіка функції з віссю ординат; (0; 5)
5) значення аргументу, при яких функція набуває від’ємних значень;
y < 0 при –5 < х < –3 і 3 < х < 5
6) значення аргументу, при яких функція набуває додатних значень.
y > 0 при –6 ≤ х < –5 і –3 < х < 3 і 5 < х ≤ 6
Завдання 922
За графіком функції y = f(x)рисунку 34 знайдіть:
1) f(–4) = 3,5; f(–2,5) = 2; f(0,5) = 0; f(2) = 0,5
2) f(х) = 2,5, якщо х = –3,5; f(х) = 1, якщо х = –2, х = 1, х = 4
f(х) = 0, якщо х = –0,5, х = 0,5, х = 2,5, х = 3,5
3) область визначення: –4 ≤ х ≤ 4,5; область значень: –1 ≤ f(х) ≤ 3,5
4) f(x) > 0 при –4 < х < –0,5; 0,5 < х < 2,5; 3,5 < х ≤ 4,5
5) f(x) < 0 при –0,5 < х < 0,5 і 2,5 < х < 3,5
Завдання 923
Чи належить графіку функції y = x² + 2 точка:
1) A(0; 2); Так, бо х = 0, у = 0² + 2 = 2
2) B(–1; 1); Ні, бо х = –1, у = (–1)² + 2 = 3, а 3 ≠ 1
3) C (–2; 6); Так, бо х = –2, у = (–2)² + 2 = 6
4) D(–3; –7)? Ні, бо х = –3, у = (–3)² + 2 = 11, а 11 ≠ –7
Завдання 924
Чи належить графіку функції y = –2x² – 1 точка:
1) A (1/2; –1,5); Так, бо х = 1/2, у = –2 • (1/2)² – 1 = –1,5
2) B(–3; 17)? Ні, бо х = –3, у = –2 • (–3)² – 1 = 3, а 3 ≠ –17
Завдання 925
Назвіть координати кількох точок, які належать графіку функції:
1) у = 7x – 4;
Якщо х = 0, то у = 7 • 0 – 4 = –4, тому точка А(0;–4) належить графіку функції.
Якщо х = 1, то у = 7 • 1 – 4 = 3, тому точка В(1;3) належить графіку функції.
2) y = x² +1;
Якщо х = 0, то у = 0² + 1 = 1, тому точка А(0;1) належить графіку функції.
Якщо х = 5, то у = 5² + 1 = 26, тому точка В(5;26) належить графіку функції.
3) у = 4 – | x |.
Якщо х = 0, то у = 4 – |0| = 4, тому точка А(0;4) належить графіку функції.
Якщо x = –4, то у = 4 – |–4| = 0, тому точка В(–4;0) належить графіку функції.
Завдання 926
Графікам яких із даних функцій належить точка A(1; 2):
1) у = 1 – 2x; Не належить, бо при х = 1, у = 1 – 2 • 1 = –1, а –1 ≠ 2
2) у = x² + 1; Належить, бо при х = 1, у = 1² + 1 = 2
3) у = 2/x; Належить, бо при х = 1, у = 2/1 = 2
4) у = 0,3x + 0,7? Не належить, бо при х = 1, у = 0,3 • 1 + 0,7 = 1, а 1 ≠ 2
Завдання 927
Чи належить графіку функції у = –x/3 точка:
1) A(9;–3); Належить, бо при х = 9, у = –9/3 = –9
2) B(6;2); Не належить, бо при х = 6, у = –6/3 = –2, а –2 ≠ 2
3) C (–1;3); Не належить, бо при х = –1, у = –(–1)/3 = 1/3, а 1/3 ≠ 3
4) D (–12;4)? Належить, бо при х = –12, у = –(–12)/3 = 4
Завдання 928
Які з фігур на рисунку 35, можуть бути графіками функцій з аргументом х? а), б)
Завдання 929
Яка з фігурна рисунку 36, може бути графіком функції з аргументом х? б)
Завдання 930
1) Побудуйте графік ламаною ABCD з вершинами A(–3;6), B(–1;2), C (3;–2), D (9;0).
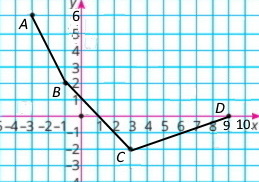
2) Якщо х = –2, то у = 4; якщо х=0, то у = 1; якщо х=2, то у = –1; якщо х=6, то у = –1
3) якщо у = 1, то х = 0; якщо у = –1, то х = 2 і х = 6; якщо у = 0, то х = 1 і х = 9
Завдання 931
Чи може ламана ABC бути графіком деякої функції, якщо:
1) A (–4; –1), B (1; 2), C (2; 4); Може бути.
2) A (–4; –1), B (1; 2), C (1; 3)? Не може бути, бо при х = 1, у набуває два значення.
Завдання 932
1) Побудуйте графік ламаної MKE, де M(–4;1), K(2;4), E(5;–2).
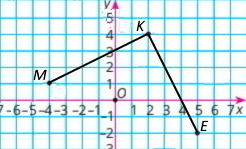
2) Якщо х = –2, то у = 2; якщо х = 0, то у = 3; якщо х = 3, то у = 2;
3) у = –2, якщо х = 5; у = 0, якщо х = 4; у = 2, якщо х = –2 і х = 3.
Завдання 933
Функцію задано формулою y = x² – 1, де –2 ≤ x ≤ 3.
1) Складіть таблицю значень функції з кроком 1.
|
x |
–2 |
–1 |
0 |
1 |
2 |
3 |
|
y |
3 |
0 |
–1 |
0 |
3 |
8 |
2) Побудуйте графік функції, користуючись складеною таблицею.
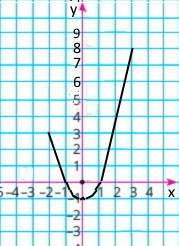
3) у < 0 при –1 < х < 1; у > 0 при –2 ≤ х ≤ –1 і 1 < х ≤ 3;
4) область значень функції –1 ≤ у ≤ 8.
Завадання 934
Функцію задано формулою у = 4 – x², де –3 ≤ x ≤ 2.
1) Складіть таблицю значень функції з кроком 1.
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
|
y |
–5 |
0 |
3 |
4 |
3 |
0 |
2) Побудуйте графік функції, користуючись складеною таблицею.
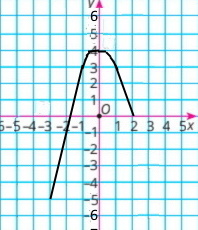
3) Користуючись графіком, знайдіть значення аргументу, при яких значення функції менші від нуля, а при яких — більші за нуль.
3) у < 0 при –3 ≤ х ≤ –2; у > 0 при –2 < х < 2;
4) область значень функції –5 ≤ у ≤ 4.
Завдання 935
Значення функції у = f (x) дорівнюють 0 при значеннях аргументу, що дорівнюють –5 і 4. Яке з наведених тверджень є правильним:
1) графік функції має з віссю ординат дві спільні точки (0;–5) і (0;4);
2) графік функції має з віссю абсцис дві спільні точки (–5;0) і (4;0)?
Завдання 936
Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) у = x² –16x;
з віссю 0х: у = 0; х² – 16х = 0; х(х – 16) = 0; х = 0 або х = 16, тому точки (0;0) і (16;0);
з віссю 0у: у = 0; у = 0² – 16 • 0 = 0, тому точка (0;0);
2) у = |x| – 2;
з віссю 0х: у = 0; |х| – 2 = 0; |х| = 2; х = –2 або х = 2, тому точки (–2;0) і (2;0);
з віссю 0у: х = 0; у = |0| – 2 = –2, тому точка (0;–2);
3) у = x3 – 9x;
з віссю 0х: у = 0; х3 – 9х = 0; х(х – 3)(х + 3) = 0; х = 0 або х = –3, або х = 3, тому
точки (0; 0), (–3;0) і (3;0);
з віссю 0у: х = 0; у = 03 – 9 • 0 = 0, тому точка (0;0);
4) у = 0,8x.
з віссю 0х і Оу: у = 0; 0,8х = 0; х = 0; точка перетину з осями координат (0;0).
Завдання 937
Не виконуючи побудови, знайдіть координати точок перетину з осями координат графіка функції:
1) у = 36 – 9x;
3 віссю 0х: у = 0; 36 – 9х = 0; 9х = 36; х = 4, тому точка (4; 0);
з віссю 0у: х = 0; у = 36 – 9 • 0 = 36, тому точка (0; 36);
2) y = x² + x;
з віссю 0х: у = 0; х² + х = 0; х(х + 1) = 0; х = 0 або х = –1, тому точки (0; 0) і (–1; 0);
з віссю 0у: х = 0; у = 0² + 0 = 0, тому точка (0; 0);
3) y = 49 – x².
з віссю 0х: у = 0; 49 – х² = 0; (7 – х)(7 + х) = 0; х = 7 або х = –7, тому точки (–7; 0) і (7; 0);
з віссю 0у: х = 0; у = 49 – 0² = 49, тому точка (0; 49).
Завдання 938
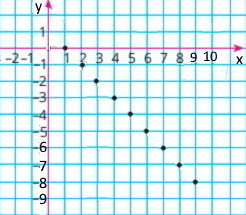
Побудуйте графік функції у = 1 – x, областю визначення якої є всі одноцифрові натуральні числа.
|
х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
у |
0 |
1 |
2 | 3 | 4 | 5 | 6 | 7 | 8 |
Завдання 939
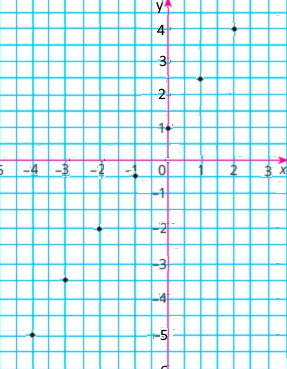
Побудуйте графік функції f(x) = 1,5x + 1, областю визначення якої є цілі числа, при яких виконується нерівність –4 ≤ x ≤ 2.
|
х |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
|
у |
–5 |
–3,5 |
–2 | –0,5 | 1 | 2,5 | 4 |
Завдання 940
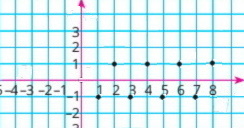
Побудуйте графік функції, областю визначення якої є всі натуральні числа та яка набуває значення 1 при парних значеннях аргументу та значення –1 при непарних значеннях аргументу.
|
х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
у |
–1 |
1 |
–1 | 1 | –1 | 1 | –1 | 1 | –1 |
Завдання 941
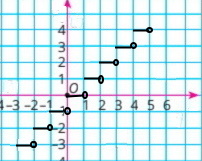
Функцію f задано описом: значення функції дорівнює найбільшому цілому числу, яке не більше за відповідне значення аргументу. Побудуйте графік цієї функції.
|
х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
у |
–1 |
1 |
–1 | 1 | –1 | 1 | –1 | 1 | –1 |
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 942
Трактористи Іван і Петро, працюючи разом, можуть зорати поле за 21 год, трактористи Петро й Остап — за 28 год, а Іван і Остап — за 20 год. За який час Іван, Петро й Остап можуть зорати це поле, працюючи втрьох?
Розв'язання
Нехай вся робота дорівнює 1. Тоді Іван і Петро за 1 год зорають разом 1/21 частини поля, Петро і Остап — 1/28 частини поля, а Іван і Остап — 1/20 частини поля.
1) 1/21 + 1/28 + 1/20 = 56/420 = 14/105 = 2/7 (ч.) – поля зорають за 1 год разом двічі;
2) 2/7 : 2 = 1/7 (ч.) – поля зорають за 1 год разом;
3) 1 : 1/7 = 7 (год) – час, за який можуть зорати поле, працюючи разом.
Відповідь: за 7 годин.
Завдання 943 Спрщення виразу
1) (c + 2)(c – 3) – (c + 1)(c + 3) = c² + 2c – 3c – 6 –(c² + 3c + c + 3) =
= c² – c – 6 – c² – 4c – 3 = –5c – 9
2) (p + 4)(p – 11) + (p + 6)² = p² – 11p + 4p – 44 + p² + 12p + 36 = 2p² + 5p – 8
3) 3(x – 5)² – (8x² – 10x) = 3(x² – 10x + 25) = 8x² + 10x = 3x² – 30x + 75 – 8x² + 10x =
= –5x² – 20x + 75
4) 7(2y – 5)² – 2(7y – 1)² = 7(4y² – 20y + 25) – 2(49y² – 14y + 1) =
= 28y² – 140y + 175 – 98y^3 + 28y – 2 = –70y² – 112y + 173
Завдання 944 Тотожність
1) (4a² + 3)² + (7– 4a²)² – 2 (4a² + 3)(4a² – 7) = 100;
(4a² + 3)² + (7– 4a²)² – 2 (4a² + 3)(4a² – 7) = ((4a² + 3) – (4a² – 7))² =
= (4a² + 3 – 4a² + 7)² = 10² = 100
2) (a² – 6ab + 9b²)(a² + 6ab + 9b²) – (a2 – 9b²)² = 0.
(a² – 6ab + 9b²)(a² + 6ab + 9b²) – (a2 – 9b²)² = (a – 3b)² (a + 3b)² – (a² – 9b²)² =
= (a² – 9b²)² – (a² – 9b²)² = 0
Завдання 945 Ознаки подільності чисел
Доведіть, що при будь–якому непарному значенні n значення виразу (4n +1)² – (n + 4)² кратне 120.
(4n + 1)² – (n + 4)² = ((4n + 1) – (n + 4))((4n + 1) + (n + 4)) =
= (3n – 3)(5n + 5) = 15(n – 1)(n + 1).
Нехай n – непарне натуральне число, тоді n – 1 і n + 1 – парні натуральні числа, причому одне з них кратне 4.
Тому добуток (n – 1)(n + 1) – кратний 8, отже, добуток 15(n – 1)(n + 1) кратний 120.
Твердження задачі доведено.
Завдання 946
Знайдіть які–небудь три натуральних значення змінної x таких, щоб вираз a² – 2x можна було розкласти на множники за формулою різниці квадратів. Отримані вирази розкладіть на множники.
1) якщо x = 2, тоді а² – 2x = а² – 4 = (a – 2)(а + 2)
2) якщо х = 8, тоді а² – 2х = а² – 16 = (a – 4)(a + 4)
3) якщо x = 18, тоді а² – 2х = а² – 36 = (a – 6)(a + 6)
Завдання 947
(Задача Бхаскари .) Є кадамба–квітка; на одну пелюстку бджілок п’ята частина сіла. Поряд росла вся у цвіту симендга, і на ній третя частина розмістилася. Різницю їхню ти знайди, тричі її ти додай, на кумай цих бджіл посади. Лише бджілка одна не знайшла собі місця ніде, усе літала туди–сюди та скрізь пахощами квітів тішилася. Тепер скажи мені: скільки бджілок усього тут зібралося?
Розв'язання
Нехай усього зібралося х бджілок. Складаємо рівняння:
x/3 + x/5 + 3(x/3 – x/5) + 1 = x
8/15x + 3 • 2x/15 + 1 = x
x – 14x/15 = 1
х/15 = 1
x = 15
Відповідь: 15 бджілок.
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
Завдання 948
У таблиці наведено відповідні значення величин x і y. Установіть, чи є ці величини прямо пропорційними.
1) х/у = 2/6 = 5/15 = 7/21 = 9/27 = 3 – величини прямо пропорційні;
2) х/у = 0,4/0,8 ≠ 1,8/3,8 – величини не є прямо пропорційними.
Завдання 949
Заповніть таблицю, якщо величина у прямо пропорційна величині x.
|
x |
0,3 |
8 |
3,2 |
0,9 |
14 |
|
y |
0,9 |
24 |
9,6 |
2,7 |
42 |
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
Завдання 950
Із квадратного аркуша паперу в клітинку, який містить цілу кількість клітинок, вирізали по лініях квадрат, що містить цілу кількість клітинок, так, що залишилася 71 клітинка. Скільки клітинок було на початковому аркуші паперу?
Розв'язання
Нехай сторона початкового квадратного аркуша паперу дорівнює х клітинок, а сторона вирізаного квадрата — у клітинок, тоді кількість клітинок у початковому квадратному аркуші паперу дорівнює х² клітинок, а у вирізаному квадраті — у².
За умовою, х² – у² = 71, або (х – у)(х + у) = 71. Оскільки 71 — просте число, то х – у = 1,
х + у = 71. Підставляємл х = у + 1 і отримуємо (у + 1) + у = 71; 2у = 70; у = 35;
х = 35 + 1 = 36. Отже, на початковому аркуші паперу було х² = 36² = 1296 клітинок.