Інші завдання дивись тут...

Завдання 838

Периметр рівностороннього трикутника та його сторона пов'язані між собою.

Якщо сторона трикутника дорівнює а, а периметр — P, то залежність змінної P від змінної а задається формулою Р = 3а.

Ця залежність є функціональною.

 

Завдання 839

Площа квадрата та його сторона пов'язані між собою.

Якщо сторона квадрата дорівнює a, а площа — S, то задати залежність змінної S від змінної a можна за формулою S = а².

Ця залежність є функціональною.

 

Завдання 840

Автомобіль рухається зі швидкістю 60 км/год. Довжина пройденого ним шляху s від часу руху t задається формулою s = 60t.

Ця залежність є функціональною, t – аргумент функції.

 

Завдання 841

У цистерні було 300 л води. Через відкритий кран щохвилини із цистерни виливається 2 л води.

Залежність об’єму V води в цистерні від часу t, протягом якого з неї виливається вода, записується так: V = 300 – 2t.

Ця залежність є функціональною. Виразимо t через V: 2t = 300 – V, t = (300 – V)/2
Область визначення цієї функції: 0 ≤ V ≤ 300
Область значень: 0 ≤ t ≤ 150

 

Завдання 842

Нехай a — довжина ребра куба, V — його об’єм. Задайте формулою залежність змінної V від змінної a. Чи є ця залежність функціональною?

Функціональна залежність між об'ємом V куба і довжиною його ребра a та задається формулою; V = а³

Ця залежність є функціональною.

 

Завдання 843

Автомобіль проїхав 120 км зі швидкістю v.

Залежність часу t від швидкості v автомобіля задається формулою: t = 120/v.  
Ця залежність є функціональною, аргументом виступає швидкість v автомобіля.

 

Завдання 844

Нехай градусні міри двох суміжних кутів дорівнюють а і р. 

Залежність ß від a записують так: ß = 180° – а

Ця залежність є функціональною, аргументом виступає кут а.
Область визначення функції: 0 ≤ а ≤ 180°

Область значень: 0 ≤ ß ≤ 180°

 

Завдання 845

У вашому класі було проведено контрольну роботу з математики. 1) Кожній дитині поставили у відповідність оцінку, яку вона отримала. 2) Кожній оцінці поставили у відповідність дитину, яка її отримала. Яке із цих правил є функцією? Функцією є правило 1), оскільки у правилі 2) кожному значенню аргументу (оцінці) відповідає не єдине значення функції (учні), позаяк одну і ту саму оцінку може мати декілька учнів.

 

Завдання 846

Розглянемо правило, згідно з яким кожному натуральному числу відповідає протилежне йому число. Чи є таке правило функцією? Так, таке правило є функцією. Кожному натуральному числу відповідає єдине, протилежне йому число.

 

Завдання 847

Кожному невід’ємному числу поставили у відповідність саме це число, а кожному від’ємному числу — число, йому протилежне. Чи є таке правило функцією?  Так, таке правило є функцією. Кожному значенню аргументу (числу) відповідає єдине значення функції.

 

Завдання 848

Кожному раціональному числу, відмінному від нуля, відповідає обернене до нього число. Чи є таке правило функцією? Так, таке правило є функцією. Кожному значенню аргументу (числу) відповідає єдине значення функції.

 

Завдання 849

Користуючись графіком залежності температури повітря від часу протягом доби, визначте:

1) О 4 год температура повітря була –4°С, о 6 год – –5°С, о 10 год – –2°С, о 18 год – 5°С, о 22 год – 0°С;
2) 5°С було о 13 год і 18 год; –2°С – о 3 год, 10 год, 23 год;
3) 0°С було о 2 год, 11 год, 22 год;
4) найнижча температура –5°С була о 6 год;
5) найвища температура 7°С була о 16 год;
6) температура повітря була нижчою від 0°С в період між 2 год та 11 год і між 22 год та 24 год, а вищою від 0°С – між 0 год та 2 год і між 11 год та 22 год;

7) температура підвищувалася від 6 год до 16 год, а знижувалася – від 0 год до 6 год та від 16 год до 24 год.

Таблиця зміни температури повітря протягом доби через кожні 2 год
t, год	0	2	4	6	8	10	12	14	16	18	20	22	24
T, °С	3	0	–4	–5	–3	–2	3	6	7	5	3	0	–3

Завдання 850

На рисунку зображено графік зміни температури розчину під час хімічного досліду.

1) Початкова температура розчину була 5°С;
2) через 30 хв після початку досліду температура розчину дорівнювала 30°С; через півтори години дорівнювала 15°С;
3) найвищою була температура 45°С через 60 хв після початку досліду;
4) температура розчину 35°С була через 40 хв та 70 хв після початку досліду.

Таблиця зміни температури розчину через кожні 10 хв протягом перших двох годин після початку досліду
t, год	0	10	20	30	40	50	60	70	80	90	100	110	120
T, °С	5	10	15	30	35	40	45	35	25	15	10	10	10

Завдання 851

На рисунку зображено графік зміни температури повітря протягом доби.

1) Температура повітря о 2 год була –5°С; о 8 год – –6°С; о 12 год – –4°С; о 16 год – 0°С; о 22 год – –2°С;
2) температура –3°С була о 14 год і 23 год; –4°С – о 0 год, о 12 год і о 24 год;
3) найнижча температура –10°С була о 6 год;
4) найвища температура 4°С була о 18 год;
5) нижчою від 0°С температура була від 0 год до 16 год та від 21 год 24 год; вищою від 0°С – від 16 год до 21 год;
6) температура повітря підвищувалася від 6 год до 18 год, а знижувалася від 0 год до 6 год та від 18 год до 24 год.

Таблиця зміни температури повітря протягом доби через кожні 2 год
t, год	0	2	4	6	8	10	12	14	16	18	20	22	24
T, °С	–4	–5	–9	–10	–6	–5	–4	–3	0	4	2	–2	–4

Завдання 852

Мотоцикліст виїхав із дому й через деякий час повернувся. На рисунку 15 зображено графік зміни відстані від мотоцикліста до дому залежно від часу (графік руху мотоцикліста).

1) За першу годину руху мотоцикліст проїхав 60 км;
2) перший раз мотоцикліст зупинився на відстані 120 км від початку руху, а другий раз – на відстані 75 км;
3) перша зупинка тривала 1 год, а друга – 30 хв;
4) через 5 год після початку руху мотоцикліст був на відстані 60 км від початку руху;
5) за останні півгодини (t = 0,5 год) мотоцикліст проїхав 45 км, тобто його швидкість становила v = 45 км : 0,5 год = 90 км/год.

 

Завдання 853

Туристка вийшла з базового табору й через деякий час повернулася. На рисунку 16 зображено графік руху туристки.

1) Через 10 год після початку руху туристка була на відстані 10 км від табору;
2) туристка витратив на зупинку 3 год;
3) туристка була на відстані 8 км від табору після виходу через 2 год;

4) до зупинки туристка пройшла 16 км за 4 год, тобто її швидкість становила 16 км : 4 год = 4 км/год;
5) за останні 2 год туристка пройшла 6 км, тобто її швидкість становила 6 км : 2 год = 3 км/год.

 

Завдання 854

Кожному числу поставили у відповідність відстань від точки, що зображає це число на координатній прямій, до початку відліку. Поясніть, чому описане правило є функцією. Знайдіть її область визначення та область значень. Позначивши цю функцію буквою f, знайдіть f (2), f (–5), f (0).

Оскільки кожному значенню аргументу (числу) ставиться у відповідність єдине значення функції (відстань від початку відліку до даної точки виражається єдиним способом), то дане правило є функцією. f(2) = 2, f(–5) = 5, f(0) = 0.

 

Завдання 855

Розглянемо функцію g, задану таким правилом: кожному одноцифровому натуральному числу поставили у відповідність останню цифру його квадрата.

1) Запишіть, чому дорівнює g (7); g (3); g (1); g (9); g (4).

7² = 49, тому g(7) = 9; 3² = 9, тому g(7) = 9; 1² = 1, тому g(1) = 1; 9² = 81, тому g(9) = 1; 4² = 16, тому g(4) = 6

2) Знайдіть область визначення та область значень функції.

Область визначення – множина натуральних чисел від 1 до 9;

Область значень – числа 1, 4, 5, 6, 9.

 

Завдання 856

Розглянемо правило, за яким числу 0 ставляться у відповідність усі парні числа, а числу 1 — усі непарні числа. Чи є це правило функцією? Ні, це правило не є функцією, оскільки кожному значенню аргументу (0 чи 1) ставиться у відповідність не єдине значення функції.

 

Завдання 857

Придумайте функцію f, областю визначення якої є всі натуральні числа, а областю значень — три числа: 0; 1; 2. Знайдіть f (7); f (15); f (101).

Функція, за якою кожному натуральному числу ставиться у відповідність остача від ділення цього числа на 3, тобто 0, 1 або 2.

f(7) = 1; f(15) = 0; f(101) = 2

 

Завдання 858

Розглянемо правило, за яким кожному натуральному числу поставили у відповідність остачу при діленні його на 7. Чи є це правило функцією? У разі ствердної відповіді знайдіть область визначення та область значень цієї функції. 

Так, це правило є функцією, оскільки кожному значенню аргументу ставиться у відповідність єдине значення функції (остача від ділення на 7). Область визначення – множина натуральних чисел, а область значень – цілі числа від 0 до 6.

 

Завдання 859

У таблиці наведено виміри температури повітря протягом доби через кожну годину . Побудуйте за цими даними графік зміни температури.

Час доби, год	0	1	2	3	4	5	6	7	8	9	10	11	12
Температура, °C	2	3	1	0	–2	–3	–5	–4	–2	0	1	4	7
Час доби, год	13	14	15	16	17	18	19	20	21	22	23	24
Температура, °C	8	9	7	5	4	3	2	1	0	–2	–3	–6

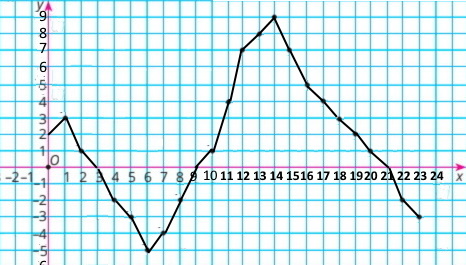
Температура підвищувалася від 0 год до 1 год та від 6 год до 14 год, а знижувалася – від 1 год до 6 год та від 14 год до 24 год.

 

Завдання 860

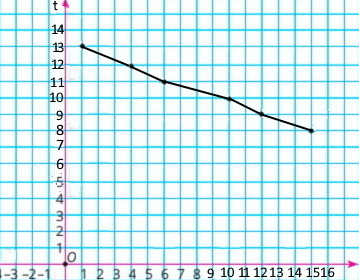
В економічних дослідженнях часто використовують криву попиту. Крива попиту — це графік, який показує, як залежить попит на товар від його ціни. У таблиці наведено залежність попиту на картоплю в деякому регіоні (у тисячах тонн) від ціни 1 кг картоплі.

Ціна 1 кг картоплі, грн	8	9	10	11	12	13
Попит, тис. т	15	12	10	6	4	1

Подайте дані, наведені в таблиці, графічно. Сполучивши отримані точки відрізками, побудуйте криву попиту на картоплю.

Завдання 861

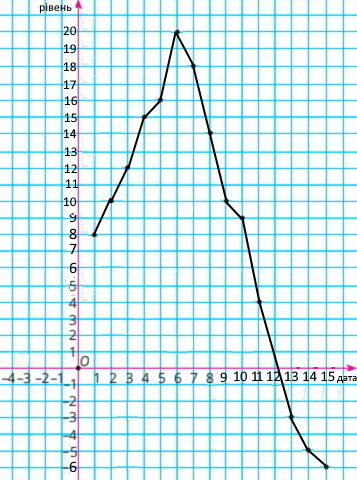
У таблиці наведено дані про рівень води в річці порівняно з ординаром (середнім рівнем води) з 1 по 15 травня.

Дата	Рівень води, см	Дата	Рівень води, см	Дата	Рівень води, см
1	8	6	20	11	4
2	10	7	18	12	0
3	12	8	14	13	–3
4	15	9	10	14	–5
5	16	10	8	15	–6

Побудуйте графік зміни рівня води в річці за вказаний час.

Завдання 862

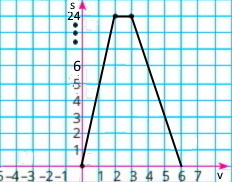
Велосипедистка виїхала з дому на прогулянку. Перші 2 год вона їхала зі швидкістю 12 км/год, потім відпочивала годину й повернулася додому зі швидкістю 8 км/год. Побудуйте графік руху велосипедистки.

Завдання 863

Початкова температура води була 6 °С. Під час нагрівання температура води підвищувалася щохвилини на 2 °С.

1) Запишіть формулу залежності температури T води від часу t її нагрівання. T = 6 + 2t

2) Складіть таблицю значень температури T за час нагрівання від 0 хв до 10 хв із кроком 1 хв.

t, °С	0	1	2	3	4	5	6	7	8	9	10
T, °С	6	8	10	12	14	16	18	20	22	24	26

3) Побудуйте графік залежності температури води від часу нагрівання протягом перших 10 хв.

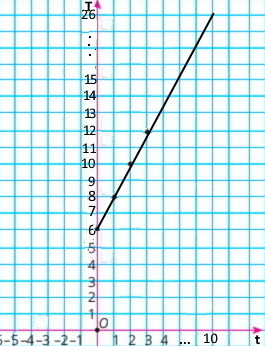
Завдання 864

Прямолінійна дорога проходить повз туристичний табір. Турист, перебуваючи на відстані 5 км від табору, почав рухатися цією дорогою зі швидкістю 4 км/год, віддаляючись від табору.

1) Знайдіть відстань s від табору, на якій перебуватиме турист через t год після початку руху.

S = 5 + 4t

2) Заповніть таблицю значень s:

t, год	0	0,25	0,5	0,75	1	1,25	1,5	1,75	2
S, км	5	6	7	8	9	10	11	12	13

3) Користуючись заповненою таблицею, побудуйте графік залежності відстані до табору від часу руху.

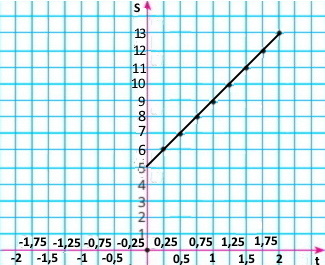
Завдання 865

У міській раді Сонячного міста представлено дві партії: партія допитливих і партія ерудитів. Усього в міській раді 20 місць. У таблиці наведено кількість депутатських місць, які отримала партія допитливих протягом 8 останніх виборів.

Вибори, №	1	2	3	4	5	6	7	8
Кількість депутатів від партії допитливих, осіб	14	12	10	16	18	15	14	10

1) Складіть подібну таблицю для партії ерудитів.

Вибори, №	1	2	3	4	5	6	7	8
Кількість депутатів від партії допитливих, осіб	6	8	10	4	2	5	6	10

2) Подайте дані кожної таблиці графічно в одній системі координат. Побудуйте «криві популярності» кожної партії, сполучивши отримані точки відрізками.

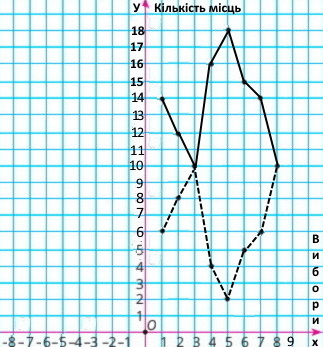
Завдання 866

У баку було 8 л гасу. Щохвилини в бак уливають 4 л.

1) Запишіть залежність кількості у літрів гасу в баку від часу x, протягом якого гас уливали в бак. у = 8 + 4х

2) Накресліть графік зміни у, надаючи x значень від 0 до 10.

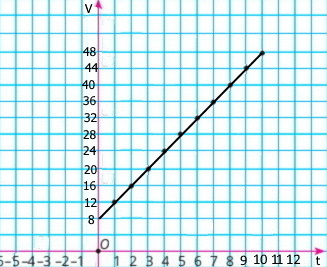
3) Користуючись графіком, визначте:

а) скільки літрів гасу буде в баку через 3 хв; через 5 хв; 20 л і 28 л відповідно.

б) через скільки хвилин у баку буде 40 л гасу. Через 8 хв.

4) Через скільки хвилин бак буде наповнено, якщо його місткість — 80 л? Через 18 хв.

 

Завдання 867

На складі було 100 т вугілля. Щодня на склад привозили 20 т вугілля.

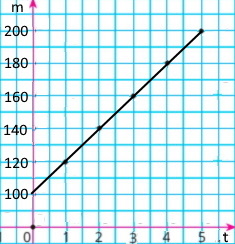
1) Виразіть формулою залежність кількості m вугілля на складі від часу t. m = 100 + 20t

2) Накресліть графік цієї залежності.

t, дні	0	1	2	3	4	5
100 + 20t	100	120	140	160	180	200

Завдання 868

Який із наведених графіків (рис. 17) ілюструє залежність змінної у від змінної x, подану нижче:

1) вартість проїзду в автобусі зростає на 1 грн через кожні 10 км шляху (x км — довжина шляху, у грн — вартість проїзду); Графік б)

2) металеву пружину розтягнули та відпустили (x с — час, у см — довжина пружини);

Графік в)

3) вартість полуниці на ринку протягом травня – червня (x днів — час, у грн — вартість)?

Графік а)

 

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

Завдання 869 Рівняння

1) –1,2x + 7,2 = 0     1,2х = 7,2     x = 6

2) –1/3х – 6 = 0     1/3х = –6     х = –18

3) 3х + 1,5 = –2,5     3х = –4     х = –4/3 = –1 1/3

4) 6 – 0,5х = 16    –0,5х = 10     х = –20

Завдання 870 Розклад на множники

1) –9/64b⁶ –3mn⁶ – 16m²n⁴ = –(9/64n⁶ + 3mn⁶ + 16m²n⁴) = –(3/8n⁶ + 4mn²)² =

= –(3/8 n⁶ + 4mn²)(3/8 n⁶ + 4mn²)

2) 20z² + 3xy – 15xz – 4yz = 5z(4z – 3x) – y(4z – 3x) = (4z – 3x)(5z – y)

3) 0,027a¹² + b⁹ = (0,3a⁴ + b³)(0,09a⁸ – 0,3a⁴b³ + b⁶)

 

Завдання 871 Ознаки подільності числа

Доведіть, що при будь–якому натуральному значенні n значення виразу:

1) (n + 25)(n + 3) – (n + 6)(n + 4) – 6 ділиться націло на 9;

(n + 25)(n + 3) – (n + 6)(n + 4) – 6 = n² + 28n + 75 – n² – 10n – 24 – 6 = 18n + 45 = 9(2n + 5) 

2) (13n – 24) (13n + 24) – (12n – 26) (12n + 26) ділиться націло на 25;

(13n – 24) (13n + 24) – (12n – 26) (12n + 26) = 169n² – 576 – 144n² + 676 = 25n² + 100 = 25(n² + 4)

3) (9n + 2)² – (3n – 2)² ділиться націло на 24.

(9n + 2)² – (3n – 2)² = 81n² + 36n + 4 – 9n² + 12n – 4 = 72n² + 48n = 24(3n² + 2n)

 

Завдання 872

Відомо, що при деякому значенні x значення виразу 2x² – 3x + 1 дорівнює 2. Знайдіть значення виразу 10x² – 15x – 20 при цьому значенні змінної x.

10x² – 15x – 20 = 5(2x² – 3x – 4) = 5(2x² – 3x + 1 – 5) = 5(2 – 5) = 5• (–3) = –15

 

Завдання 873

Знайдіть таке найменше натуральне значення a, при якому вираз x² – 4x + 2а набуває додатних значень при будь–якому значенні x.

x² – 4х + 2а = х² – 4х + 4 + 2а – 4 = (х – 2)² + 2а – 4

Вираз набуває невід'ємних значень для будь–якого х при 2а – 4 = 0, звідси а = 2. Вираз набуває додатніх значень при а > 2, тому найменше значення а = 3. 

 

Завдання 874

У готелі є тільки одномісні та двомісні номери. На кожні 3 одномісних номери припадає 2 двомісних.

1) Скільки відсотків становить кількість одномісних номерів від загальної кількості номерів?

За умовою, на кожні 3 одномісних номери припадає 2 двомісних,  означає, що: 

3x + 2x = 5x (н.) – всього номерів;

3x/5x • 100% = 0,6 • 100% = 60% – відсоток одномісних номерів.

Відповідь: 60%.

2) Скільки всього місць в готелі, якщо є 34 двомісних номери?

1) 34 : 2 = 17 (н.) – припадає на одну частину;

2) 3 • 17 = 51 (н.) – одномісниx номерів у готелі;

3) 34 • 2 = 68 (м.) – місць у двомісних номерах;

4) 51 + 68 = 119 (м.) – загальна кількість місць в готелі.

Відповідь: 119 місць.

 

УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ

Завдання 875

Натуральні числа x і у такі, що 34x = 43у. Доведіть, що число x + у складене.

Оскільки 43 – просте число, то одним із розв'язків рівняння 34х = 43у є пара чисел: х = 43, у = 34.
Усі інші розв'язки будуть кратні знайденим. Наприклад, числу 2 кратними є х = 86, у = 68 і т.д.
Якщо х + у = 43 + 34 = 77, а число 77 – складене;

Якщо х + у = 86 + 68 = 154, а число 154 – складене і т.д.

Інші завдання дивись тут...