Контрольна робота 5, тип 2.
Варіант І
Завдання 1. Хибне твердження.
А сто сорок тисяч сімсот — це 140 700
Б сто сорок тисяч сімдесят — це 14 070
В сто сорок сім тисяч сімсот — це 147 700
Завдання 2. Число 20 580 більше за 140 у … разів
Б у 147 разів
_20580 | 140
140 147
_658
560
_980
980
0
Завдання 3. Яку відстань можна пройти за 5 год зі швидкістю 65 км/год?
Б 325 км
Міркуємо так.
Розв'язання.
1) 65 • 5 = (60 + 5) • 5 = 325 (км) – відстань можна пройти.
Відповідь: 325 кілометрів.
Завдання 4.
a = 123 -----------> 9507
a = 321 ------------> 8913
a = 231 -----------> 9183
Розв'язання.
Якщо а=123, тоді 9876 - 3 • 123 = 9876 - 369 = 9507
Якщо а=321, тоді 9876 - 3 • 321 = 9876 - 963 = 8913
Якщо а=231, тоді 9876 - 3 • 231 = 9876 - 693 = 9183
Зміни 2020 року видання. Завдання 5. Порівняй.
23 000 г < 2 ц (2 ц = 200 кг = 200000 г, а 23000 г < 200000 г)
230 кг > 2 ц (2 ц = 200 кг, а 230 кг>200 кг)
2 ц > 2 кг (2 ц = 200 кг, а 200 кг>2 кг)
Завдання 5.
23000 г < 2 ц 230 кг > 2 ц
Міркуємо так.
|
2 ц = 200 кг = 200000 г 23 000 г < 200 000 г |
2 ц = 200 кг 230 кг > 200 кг |
Величини 23 000 г, 2 ц, 230 кг у порядку зростання:
23000 г, 2 ц, 230 кг
Міркуємо так.
23000 г = (23000 : 1000) кг = 23 кг
2 ц = 200 кг
230 кг
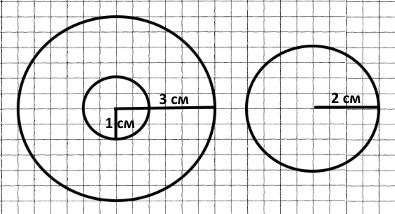
Завдання 6. Побудуй коло, радіус якого дорівнює різниці радіусів заданих кіл.
Радіус великого кола — 3 см.
Радіус малого кола — 1 см
3 см – 1 см = 2 см – радіус кола для побудови.
Завдання 7. Поле засіяли пшеницею, житом і ячменем. Житом засіяли 51 га поля, ячменем — на 17 га менше, а пшеницею засіяли стільки, скільки житом і ячменем разом. Знайди площу поля.
Розв'язання.
1) 51 – 17 = 34 (га) — площу поля засіяли ячменем.
2) 51 + 34 = 85 (га) — площу поля засіяли пшеницею.
3) 51 + 34 + 85 = 170 (га) — площа поля.
Відповідь: 170 га площа.
Зміни 2020 року видання. Завдання 8 Запиши всі трицифрові числа, використовуючи цифри 0, 3 і 5
302, 305, 350, 353, 503, 505, 530, 535
Міркуємо так.
Щоб не помилитися, застосуємо метод побудови дерева.
Знайдемо усі трицифрові числа з цифрою 3 на початку.
3
/ \
0 5
/ \ / \
3 5 0 3
Маємо 303, 305, 350, 353
Знайдемо усі трицифрові числа з цифрою 5 на початку.
5
/ \
0 3
/ \ / \
3 5 0 5
Маємо 503, 505, 530, 535