Інші завдання дивись тут...

Завдання 227 Множення чисел

20 • 6 = 120 25 • 4 = 100

300 • 4 = 1200 33 • 2 = 66

5 • 60 = 300 12 • 30 = 360

6 • 300 = 1800 200 • 4 = 800

Завдання 228 Ділення чисел

1) 240 : 3 = 80

    50 : 6 = 8 (ост. 2).

2) Наведіть власні приклади на ділення без остачі та ділення з остачею. Перевірте одне одного.

    250 : 5 = 50

    251 : 5 = 50 (ост. 1)

 

Завдання 229

1. 120 : (2 • 3) = 120 : 2 : 3 = 60 : 3 = 20

2. (48 + 36) : 6 = 48 : 6 + 36 : 6 = 8 + 6 = 14

3. (90 – 21) : 3 = 90 : 3 – 21 : 3 = 30 – 7 = 23

 

Завдання 230

Якщо дільник дорів­нює 1, то частка дорівнює діленому.

Якщо ділене дорівнює 0, то частка дорівнює нулю.

Якщо діль­ник дорівнює діленому, то частка дорівнює одиниці.

 

Завдання 231

693 : 3 = (600 + 90 + 3) : 3 = 600 : 3 + 90 : 3 + 3 : 3 = 200 + 30 + 1 = 231

836 : 4 = (800 + 36) : 4 = 800 : 8 + 36 : 4 = 200 + 9 = 209

645 : 5 = (500 + 100 + 45) : 5 = 500 : 5 + 100 : 5 + 45 : 5 = 100 + 20 + 9 = 129

246 : 6 = (240 + 6) : 6 = 240 : 6 + 6 : 6 = 40 + 1 = 41

450 : 6 = (420 + 30) : 6 = 420 : 6 + 30 : 6 = 70 + 5 = 75

 

Завдання 232

На одноколісному скейті хлопчик проїхав 36 км за 3 год. Скільки кілометрів він зможе проїхати за 2 год, якщо збільшить швидкість на 2 км/год?

Швидкість	Час	Відстань
?	3 год	36 км
?, на 2 км/год більше	2 год	?

Розв'язання

1) 36 : 3 = 12 (км/год) – швидкість спочатку;

2) 12 + 2 = 14 (км/год) – швидкість потім.

3) 14 • 2 = 28 (км)

Відповідь: хлопчик зможе проїхати 28 км.

 

Завдання 233

Електромопед за 5 год проїхав 60 км. Першу половину шляху він їхав зі швидкістю 15 км/год. На скільки менша була його швидкість на дру­гій половині шляху?

Шлях	Швидкість		Час	Відстань
I половина	15 км/год	На ?	5 год	60 км
II половина	?

Розв'язання

1) 60 : 2 = 30 (км) – половина шляху;

2) 30 : 15 = 2 (год) – витратив часу на першу половину шляху;

3) 5 – 2 = 3 (год) – витратив часу на другу половину шляху;

4) 30 : 3 = 10 (км/год) – швидкість на другій половині шляху.

5) 15 – 10 = 5 (км)

Відповідь: на 5 км/год була менша його швидкість на другій половині шляху.

 

Завдання 234 Письмове ділення

Невідоме число зменшили в 3 рази, а потім результат збільшили на 240 і одержали 720.

х : 3 + 240 = 720

х : 3 = 720 – 240

х : 3 = 480

х = 480 • 3

х = 1440

Число 640 зменшили на добуток невідомого числа й числа 8. Одержали 240.

640 – 8 • х = 240

8 • х = 640 – 240

8 • х = 400

х = 400 : 8

х = 50

 

Завдання 236

За 2 дні туристи в горах пройшли 24 км. Пер­шого дня вони пройшли у 3 рази більшу від­стань, ніж другого. Скільки кілометрів вони проходили кожного дня?

^{Короткий запис}

^{Відстань — 24 км}

^{I дн. — ?, у 3 р. більшу відстань, ніж II дн.}

^{II дн. — ?}

Розв'язання

1–й спосіб

1) 1 + 3 = 4 (ч.) – частин припадає на весь шлях;

2) 24 : 4 = 6 (км) – відстань пройшли II дня;

3) 6 • 3 = 18 (км) – відстань пройшли I дня.

2–й спосіб

1) 1 + 3 = 4 (ч.) – частин припадає на весь шлях;

2) 24 : 4 = 6 (км) – відстань пройшли II дня; 

3) 24 – 6 = 18 (км) – відстань пройшли I дня.

Відповідь: туристи пройшли першого дня 18 км, а другого дня 6 км. 

 

Завдання 237

Накресли коло. На ньому постав 5 точок. Через них попарно проведи прямі.

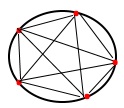
Скільки прямих? 10

 

Завдання 238

За день туристи пройшли 31 км. 4 год вони йшли зі швидкістю 4 км/год, а решту шляху — зі швидкістю 5 км/год. Скільки часу туристи були в дорозі?

Швидкість	Час		Відстань
4 км/год	4 год	?	31 км
5 км/год	?

Розв'язання

1) 4 • 4 = 16 (км) – відстань пройшли спочатку;

2) 31 – 16 = 15 (км) – відстань пройшли потім;

3) 15 – 5 = 3 (год) – час в дорозі потім.

4) 3 + 4 = 7 (год)

Відповідь: туристи були в дорозі 7 год.

 

Завдання 239 Письмове ділення

1) 8 : 3 = 2 (ост. 2)

24 дес. : 5 = 240 : 5 = (200 + 40) : 5 = 40 + 8 = 48

9 сот. : 4 = 900 : 4 = (800 + 80 + 20) : 4 = 200 + 20 + 5 = 225

17 тис. : 5 = 17000 : 5 = (15000 + 2000) : 5 = 3000 + 400 = 3400

2) Остача може бути при діленні на 5: 0, 1, 2, 3, 4

Остача може бути при діленні на 8: 0, 1, 2, 3, 4, 5, 6, 7

Остача може бути при діленні на 9: 0, 1, 2, 3, 4, 5, 6, 7, 8

 

Завдання 241 Письмове ділення

Найвища гора Карпат — Говерла — має висо­ту 2061 м. Це на 24 м більше, ніж висота гори Бребенеска, і на 60 м більше, ніж висота гори Ребра. Яка із цих гірських вершин Карпат найнижча?

Короткий запис

Говерла — 2061, це на 24 м більше, ніж Бребенеска, і на 60 м більше, ніж Ребра

Бребенеска — ?

Ребра — ?

Яка найнижча — ?

Розв'язання

1) 2061 – 24 = 2037 (м) – висота гори Бребенеска;

2) 2061 – 60 = 2001 (м) – висота гори Ребра.

Відповідь: гора Ребра найнижча.

 

Завдання 245 Ознайомлення з дробами

Яку частину прямокутного паралелепіпеда на кожному малюнку вирізано?

1/4 (одна четверта), 1/9 (одна дев'ята), 1/18 (одна вісімнадцята)

 

Завдання 246

Щоб утекти від ворога, мураха одного з видів ніби «вистрілює» щелепою в землю і відлітає від нападника на 2/25 метра по вертикалі й у 5 разів далі по горизонталі. На яку відстань мураха відлітає від ворога по горизонталі?

^{Короткий запис}

^{По вертикалі — ?, 2/25 метра}

^{По горизонталі — ?, у 5 разів більше, ніж по вертикалі}

Розв'язання

1 м = 100 см

1) 100 см : 25 • 2 = 4 • 2 = 8 (м) – відстань по вертикалі;

2) 8 • 5 = 40 (м) – відстань по горизонталі.

Відповідь: на 40 м мураха відлітає від ворога по горизонталі.

 

Завдання 247

За перший рік корінь дуба виростає на 1 м у глибину. Наступні 10 років він щороку виростає на стільки само. Якою буде довжина кореня через 10 років?

^{Короткий запис}

^{За 1 р. — 1 м}

^{За 10 р. — ?, щороку на стільки ж}

Розв'язання

1 • 10 = 10 (м)

Відповідь: довжина кореня буде 10 м через 10 років.

 

Завдання 248

За перший рік молодий дубок виростає на 14 см, а потім щорічно до 10 років виростає на половину цієї довжини. Після 10 років його висота щорічно збільшується на величину, що становить 2/5 метра. Яка може бути висота 50–річного дуба?

^{Короткий запис}

^{За 1 р. — 14 см}

^{Щорічно до 10 р. — ?, 1/2 довжини}

^{Щорічно після 10 р. — ?, 2/5 метра}

^{Всього після 50 р. — ?}

Розв'язання

1 м = 100 см

1) 14 : 2 = 7 (см) – половина довжини;

2) 14 + 7 • 9 = 14 + 63 = 77 (см) – довжина дуба до 10 років включно;

3) 100 : 5 • 2 = 20 • 2 = 40 (см) – становить довжина 2/5 метра;

4) 50 – 11 + 1 = 40 (р.) – вік від 11 до 50 років; 

5) 40 • 40 = 1600 (см) – довжина дуба від 11 до 50 років.

6) 1600 + 77 = 1677 (см) = 16 м 77 см

Відповідь: висота 50–річного дуба може бути 16 м 77 см.

 

Завдання 249

Довжина стрибка вивірки звичайної (білки) сягає 6 м, а білки–летяги — у 5 разів більша. За скільки стрибків білка звичайна подолає відстань, яку білка–летяга долає за три стрибки?

	Довжина 1 стрибка	Кількість стрибків	Відстань
Білка звичайна	6 м	?	Однакова
Білка–летяга	?, у 5 разів більше	3

Розв'язання

1) 6 • 5 = 30 (м) – довжина стрибка білки–летяги;

2) 30 • 3 = 90 (м) – відстань кожної.

3) 90 : 6 = 15 (стр.)

Відповідь: за 15 стрибків білка звичайна подолає цю відстань.

 

Завдання 250

Інші завдання дивись тут...