ГДЗ Лишенко 4 клас математика Завдання 1 – 8 Додаткові вправи Частина 2 Відповіді до підручника нова програма 2021

Завдання 1

Поясни рівність x : 7 = 42 : 21 за таблицею. Розв'яжи задачу іншим способом.

^Ціна	^{Кількість}	^{Вартість}
^{Однакова}	^{6 з.}	^{21 грн}
^{Однакова}	^?	^{42 грн}

x : 7 = 42 : 21 – однакова ціна зошита.

1 спосіб

42 : х = 21 : 7

42 : х = 3

х = 42 : 3

х = 14 (з.)

2 спосіб

1) 21 : 7 = 3 (грн.) – ціна зошита.

2) 42 : 3 = (30 + 12) : 3 = 10 + 4 = 14 (з.) – купили інших зошитів.

Відповідь: купили 14 зошитів.

Завдання 2

Автомобіль долає 360 км за 6 год. На скільки йому треба збільшити швидкість, щоб подолати цю відстань на 1 год швидше?

^{Швидкість}	^Час	^{Відстань}
^?	^{6 год}	^{360 км}
^?	^{?, на 1 год менше}	^{380 км}

Розв’язання

1) 6 – 1 = 5 (год) – час руху зі збільшеною швидкістю.

2) 360 : 6 = 60 (км/год) – початкова швидкість.

3) 360 : 5 = 72 (км/год) – збільшена швидкість.

4) 72 – 60 = 12 (км/год)

Відповідь: на 12 км/год треба збільшити швидкість.

Завдання 3

1. За 3 с спортсмен пробіг 10 м. Скільки метрів він пробіжить за хвилину?

Короткий запис

3 с — 10 м

60 с — ?

Розв'язання

1) 60 : 3 = 20 (р.) – у стільки разів більше пробіжить.

2) 10 • 20 = 200 (м) – пробіжить спортсмен за 60 с.

Відповідь: за хвилину спортсмен пробіжить 200 метрів.

2. Першого дня посадили 3 ряди груш. Другого дня посадили 4 ряди яблунь по 50 дерев порівно в кожному ряду. Скільки садили груш у одному ряду, якщо всього посадили 440 фруктових дерев?

Короткий запис

І — 3 р. груш по ? д.

ІІ — 4 р. по 50 д.

Усього — 440 д.

Розв'язання

1) 50 • 4 = 200 (д.) – посадили яблунь.

2) 440 – 200 = 240 (д.) – посадили груш.

3) 240 : 3 = 80 (д.) – груш у одному ряді.

Відповідь: у одному ряду 80 груш.

Завдання 4

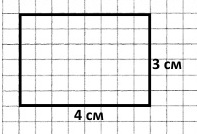
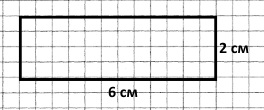
Накресли два прямокутники, що мають однакові площі, але різні сторони. Знайди їхні периметри.

Розв'язання