ГДЗ 4 клас Заїка математика завдання 221 – 230 Частина 2 Нова програма 2021 року Відповіді до підручника Ответы к учебнику

Інші завдання дивись тут...

Завдання 221

а) Уляна купила 20 зошитів за ціною 2 грн кожний. Яка вартість покупки?

б) Уляна купила 20 однакових зошитів за 40 грн. Яка ціна зошита?

Розв'язання

40 : 20 = 2 (грн)

Відповідь: ціна зошита 2 грн.

в) Уляна купила на 40 грн зошити за ціною 2 грн кожний. Скільки зошитів купила Уляна?

Розв'язання

40 : 2 = 20 (з.)

Відповідь: Уляна купила 20 зошитів.

Завдання 222

360 : 9 = 40

424 : 4 = (400 + 24) : 4 = 100 + 6 = 106

24 000 : 24 = 24 тис. : 24 = 1 тис = 1000

3200 : 8 = 32 тис. : 8 = 4 тис. = 400

Завдання 223 Розрядні доданки

1) 365 : 5 = (300 + 60 + 5) : 5 = 60 + 12 + 1 = 73 — розкладено на розрядні доданки

2592 : 8 = (2400 + 160 + 32) : 8 = 300 + 20 + 4 = 324 — розкладено на зручні доданки

2) 741 : 3 = (600 + 120 + 21) : З = 200 + 40 + 7 = 247

Завдання 224, 225 Письмове ділення

_10725 | 5

10 245

_22

_25

_592 | 8

56 74

_32

_22736 | 7

21 3248

_17

_33

_56

_2466 | 9

18 274

_66

_36

_2492 | 7

21 356

_39

_42

Завдання 226

7 • 6 < 43

5 • 7 < 38

9 • 6 < 60

8 • 8 < 70

7 • 3 < 24

4 • 8 < 33

6 • 5 < 35

8 • 6 < 49

Завдання 227

Свій день народження Сергійко збирається відсвяткувати, подорожуючи з батьками Європою. Для цієї поїздки вони обміняли валюту.

1) Скільки польських злотих сім’я зможе купити за 22 785 грн, якщо ціна одного злотого 7 грн?

^{Короткий запис}

^{1 зл. — 7 грн}

^{? — 22785 грн}

Розв'язання

_22785 | 7

21 3255 (зл.)

_17

_38

_35

Відповідь: сім'я може купити 3255 злотих.

2) Повернувшись в Україну, вони обміняли 150 злотих (залишок) на гривні. Скільки гривень сім’я повернула, якщо під час здачі в банк 1 злотий коштував 6 грн?

^{Короткий запис}

^{1 зл. — 6 грн}

^{150 зл. — ?}

Розв'язання

150 • 6 = (100 + 50) • 6 = 600 + 300 = 900 (грн)

Відповідь: сім'я повернула 900 грн.

Завдання 228

Для святкування Дня іменинника в класі купили 7 пачок зефіру, по 250 г кожна, 8 пакетів цукерок, по 350 г кожний.

а) Чого куплено більше і на скільки?

^{Короткий запис}

^{Зефіру — ?, 7 п. по 250 г кожна}

^{Цукерок — ?, 8 п. по 350 г кожний, на скільки більше — ?}

Розв'язання

1) 250 • 7 = 1750 (г) – маса зефіру.

2) 350 • 8 = 2800 (г) – маса цукерок.

3) 2800 – 1750 = 1050 (г) = 1 кг 50 г

Відповідь: на 1 кг 50 г більша маса цукерок, ніж зефіру.

б) Чому дорівнює маса куплених солодощів?

Розв'язання

1750 + 2800 = 4550 (г) = 4 кг 550 г

Відповідь: куплено 4 кг 550 г солодощів.

в) Ціна пачки зефіру 9 грн, ціна пакета цукерок — 18 грн. Вартість яких солодощів більша й на скільки? Яка вартість усіх куплених солодощів?

Розв'язання

1) 9 • 7 = 63 (грн) – вартість зефіру.

2) 18 • 8 = 144 (грн) – вартість цукерок.

3) 144 – 63 = 81 (грн) – на стільки більша вартість цукерок, ніж зефіру.

4) 63 + 144 = 207 (грн) – вартість усіх куплених солодощів.

Відповідь: на 81 грн більша вартість цукерок, ніж зефіру; солодощів куплено на 207 грн.

Завдання 229

37 + 37 + 37 + 37 + 37 + 37 + 37 + 37 + 37 + 37 = 37 • 10 = 370

117 + 883 + 117 + 883 + 117 + 883 + 117 + 883 = (117 + 883) • 4 = 1000 • 4 = 4000

(5 • 5015) • 2 = 5 • 2 • 5015 = 10 • 5015 = 50150

2 • (2 • 370) • 25 = 2 • 2 • 25 • 370 = 4 • 25 • 370 = 100 • 370 = 37000

249 • 5 + 249 • 5 = 5 • (249 + 1) = 5 • 250 = 4 • 250 + 250 = 1000 + 250 = 1250

Завдання 230

Розміри шести прямокутників виражені в сантиметрах. Периметр кожного прямокутника 24 см. Побудуй той з них, який має найбільшу площу.

24 : 2 = 12 (см) – сума довжини і ширини прямокутника.

1) Довжини сторін: 11 см і 1 см. Площа: 1 • 11 = 11 (см²)

2) Довжини сторін: 10 см і 2 см. Площа: 2 • 10 = 20 (см²)

3) Довжини сторін: 9 см і 3 см. Площа: 3 • 9 = 27 (см²)

4) Довжини сторін: 8 см і 4 см. Площа: 4 • 8 = 32 (см²)

5) Довжини сторін: 7 см і 5 см. Площа: 5 • 7 = 35 (см²)

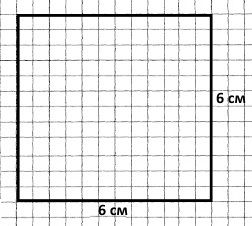
6) Довжини сторін: 6 см і 6 см. Площа: 6 • 6 = 36 (см²)

Нйбільшу площу має квадрат зі стороною 6 см.

Інші завдання дивись тут...

ГДЗ 4 клас Заїка математика завдання 221 – 230 Частина 2 Нова програма 2021 року Відповіді до підручника Ответы к учебнику

Додавання коментаря