Завдання 630
На тарілці є 2 червоні та 2 жовті яблука. Скількома способами з тарілки можна взяти:
1) 1 яблуко; 4 способи
2) 2 жовті яблука; 1 спосіб
3) 2 яблука різних кольорів? 2 способи
Завдання 631 Комбінаторика
Запишіть усі двоцифрові числа, використовуючи тільки цифри 0, 3, 5, якщо в записах чисел цифри:
1) не мають повторюватися; 30, 35, 50, 53
2) можуть повторюватися. 30, 33, 35, 50, 53, 55
Завдання 632
Запишіть усі двоцифрові числа, використовуючи тільки цифри 1, 2, 5, якщо в записах чисел цифри не мають повторюватися. 12, 15, 21, 25, 51, 55
Завдання 633
Запишіть усі трицифрові числа, використовуючи кожну з цифр 1, 4, 8 лише один раз. Скільки існує таких чисел?
148, 184, 418, 481, 814, 841 Існує шість таких чисел.
Завдання 634
Запишіть усі трицифрові числа, використовуючи кожну з цифр 0, 3, 6 лише один раз. Скільки існує таких чисел?
306, 360, 603, 630 Існує чотири таких числа.
Завдання 635
Із пункту A до пункту C ведуть різні дороги (рис. 35). Скількома різними маршрутами можна проїхати з пункту A до пункту C? Знайдіть довжину найкоротшого маршруту.
Маршрути: ABPMC, ABPNC, ADPNC, ADPMC
Від пункту А до пункту С є чотири маршрути.
Найкоротший маршрут: ABPMC (37 + 22 + 26 + 17 = 102 (км)
Завдання 636
Скільки різних двоцифрових чисел можна записати за допомогою цифр 0, 1, 2, 3, якщо в записах чисел цифри можуть повторюватися?
Відповідь: 12 двоцифрових чисел (10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33).
Завдання 637
Скільки різних двоцифрових чисел можна записати за допомогою цифр 1, 2, 3, 4, якщо в записах чисел цифри не мають повторюватися?
Відповідь: 12 двоцифрових чисел (12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43).
Завдання 638
Скількома способами можна вишикувати в одну шеренгу двох дівчат і одного хлопця так, щоб дівчата не стояли поруч?
Відповідь: 1 способом (дівчинка хлопець дівчинка).
Завдання 639
Із 3 дівчат і 2 хлопців потрібно сформувати дует, до якого входила б одна дівчина та один хлопець. Скількома способами це можна зробити?
Розв’язання
Позначимо двох хлопців: Х1, Х2
Позначимо трьох дівчат: Д1, Д2, Д3
Маємо комбінації: Х1Д1, Х1Д2, Х1Д3, Х2Д1, Х2Д2, Х2Д3
Відповідь: 6 способами.
Завдання 640
Юрко має три різні футболки і двоє різних шортів. Скільки в нього є варіантів вибрати форму для гри у футбол?
Розв’язання
Позначимо три футболки: Ф1, Ф2, Ф3
Позначимо двоє шортів: Ш1, Ш2
Маємо комбінації: Ф1Ш1, Ф1Ш2, Ф2Ш1, Ф2Ш2, Ф3Ш1, Ф3Ш2
Відповідь: 6 варіантів.
Завдання 641
Державні прапори деяких країн містять три вертикальні смуги трьох різних кольорів. Скільки є різних варіантів прапорів зі смуг білого, синього й зеленого кольорів?
Розв’язання
Позначимо три кольори: Б, С, З
Маємо комбінації: БСЗ, БЗС, СБЗ, СЗБ, ЗБС, ЗСБ
Відповідь: 6 варіантів.
Завдання 642
Водій має перевезти товар з бази в три магазини. Скільки він може скласти різних маршрутів, які відрізнялися б порядком відвідування цих магазинів?
Розв’язання
Позначимо три магазини: М1, М2, М3
Маємо комбінації: М1М2М3, М1М3М2, М2М1М3, М2М3М1, М3М1М2, М3М2М1
Відповідь: 6 маршрутів.
Завдання 643
На вершину гори веде чотири стежки. Скількома способами турист може зійти на вершину гори однією стежкою, а спуститися — іншою?
Розв’язання
Позначимо чотири стежки: 1, 2, 3, 4
Маємо комбінації: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43
Відповідь: 12 способів.
Завдання 644
Із міста А до міста В ведуть три дороги. Скільки можна дібрати різних маршрутів, щоб дістатися з міста А до міста В й повернутися назад?
Розв’язання
Позначимо три дороги: 1, 2, 3
Маємо комбінації: 11, 12, 13, 22, 23, 21, 31, 32, 33
Відповідь: 9 маршрутів.
Завдання 645
Оленка хоче зафарбувати букви в слові «мама» так, щоб дві букви мали синій колір, а дві — жовтий. Скількома способами вона може це зробити? М А М А
Розв’язання
Позначимо два кольори : СЖ
Маємо комбінації: ССЖЖ, СЖЖС, ЖЖСС, ЖСЖС, СЖСЖ, ЖССЖ
Відповідь: 6 способів.
Завдання 646
Четверо друзів збираються грати у футбол. Скількома способами вони можуть розділитися на дві команди по 2 хлопці в кожній?
Розв’язання
Позначимо четверо друзів: 1, 2, 3, 4
Маємо комбінації: 12 34, 13 24, 14 23
Відповідь: 3 способи.
Завдання 647
Іванко має 2 різні шоколадні цукерки і 2 різні льодяники. Скількома способами він може дати сестричці дві цукерки: одну шоколадну цукерку й один льодяник?
Розв’язання
Позначимо дві цукерки: Ц1, Ц2
Позначимо два льодяники: Л1, Л2
Маємо комбінації: Ц1Л1, Ц1Л2, Ц2Л1, Ц2Л2
Відповідь: 4 способи.
Завдання 648
На рисунку 36 зображено 6 карток з цифрами. 1 2 3 4 5 6.
Скількома способами із цих карток можна вибрати:
1) 2 картки з цифрами одного кольору; 4 способи (12, 23, 23, 45)
2) 3 картки з цифрами різних кольорів; 6 способів (146, 156, 246, 256, 346, 356)
3) 2 картки з цифрами різних кольорів? 11 способів (14, 15, 16, 24, 25, 26, 34, 35, 36, 46, 56)
Завдання 649
У вазі лежать 5 яблук сорту «антонівка» та по одному яблуку сорту «ренет» і «білий налив». Скількома способами з вази можна взяти 2 яблука різного сорту?
Розв’язання
Позначимо яблука сорту антонівка: 1, 2, 3, 4, 5
Позначимо яблука «ренет» і «білий налив»: р, н
Маємо комбінації: 1р, 1н, 2р, 2н, 3р, 3н, 4р, 4н, 5р, 5н, рн
Відповідь: 11 способів.
Завдання 650
Два пасажири сідають у трамвай, у якому 3 вагони. Скількома способами пасажири можуть розміститися по вагонах?
Розв’язання
Відповідь: 6 способів.
Завдання 651
Скількома способами можна помістити у дві кишені три різні монети?
Розв’язання
Відповідь: 8 способів.
Завдання 652
У кіоску продають 4 види календариків. Скількома способами можна вибрати для купівлі 2 різні календарики?
Розв’язання
12, 13, 14, 23, 24, 34
Відповідь: 6 способів.
Завдання 653
Скільки є чотирицифрових чисел, у кожному з яких сума цифр дорівнює 3?
Розв’язання
1110, 1101, 1011, 1200, 1020, 1002, 2100, 2010, 2001, 3000
Відповідь: 10 чисел.
Завдання 654
Скільки є п’ятицифрових чисел, у кожному з яких сума цифр дорівнює 2?
Розв’язання
10001, 10010, 10100, 11000, 20000
Відповідь: 5 чисел.
Завдання 655
Під час зустрічі 4 приятелі потиснули один одному руки. Скільки було рукопотискань? (Зауважимо, що коли перший приятель потискує руку другому, то це означає, що й другий потискує руку першому.
Розв’язання
12, 13, 14, 23, 24, 34
Відповідь: 6 рукопотискань.
Завдання 656
У саду ростуть чотири види фруктових дерев: 5 яблунь, 3 вишні; слив менше, ніж вишень, але більше, ніж груш. Скільки всього фруктових дерев росте в саду?
Короткий запис
Яблунь — 5
Вишень — 3
Слив — ?, менше від вишень, але більше груш.
Груш — ?
Разом — ?
Розв’язання
1) 3 – 1 = 2 (д.) – слив росте.
2) 2 – 1 = 1 (д.) – груш росте.
3) 5 + 3 + 2 + 1 = 11 (д.) – всього дерев росте.
Відповідь: 11 дерев.
Вправи для повторення
Завдання 657 Порядок дій
1) 548 204 + 490 196 = 1038400
2) 81 004 – (9046 – 1996) = 81 004 – 7050 = 73954
Завдання 658
9а – 21 > 4а + 3, якщо а = 5, бо 24 > 23
9 • 5 – 21 = 45 – 21 = 24
4а + 3 = 4 • 5 + 3 = 20 + 3 = 23
Завдання 659 Побудуйте відрізок завдовжки:
1) 6 см;
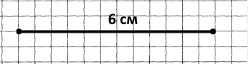
2) 4 см 8 мм.

Завдання 660
На канікулах Ігор прочитав книжку за 3 дні: першого дня він читав 1 год, другого — 3 год і третього — 4 год. Скільки сторінок має книжка, якщо першого дня Ігор прочитав на 36 сторінок менше, ніж третього?
Розв’язання
1 спосіб
1) 4 – 1 = 3 (год) – на стільки менше прочитав першого дня, ніж третього.
2) 36 : 3 = 12 (стор.) – прочитав за 1 год.
3) 1 + 3 + 4 = 8 (год) – весь час, що читав книжку.
4) 12 • 8 = 96 (с.)
2 спосіб
Нехай за 1 год Ігор читає х сторінок, тоді за 4 год — 4х сторінок. Складаємо рівняння: