Початковий рівень
Вправа 1 На одному з рисунків зображено кут, величина якого дорівнює 70°. Укажіть цей кут. В
Вправа 2. Яку координату має точка A координатного променя ОХ? Б 4
Вправа 3 Знайдіть периметр трикутника, сторони якого дорівнюють 3 см, 4 см і 5 см.
Г 12 см 3 + 4 + 5 = 12 (см)
Вправа 4 Знайдіть площу прямокутника, сторони якого дорівнюють 11 см і 10 см.
Б 110 см2 11 • 10 = 110 (см2)
Вправа 5 Знайдіть площу поверхні куба з ребром 5 мм. В 150 мм2
5 • 5 • 6 = 25 • 6 = 150 (мм2)
Вправа 6 Знайдіть об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 4 дм, 6 дм і 5 дм. Г 120 дм3
4 • 5 • 6 = 20 • 6 = 120 (дм3)
Середній рівень
Вправа 7 Кут AОB — прямий (див. рис.). Знайдіть величину кута АОС, якщо ∠СОВ = 25°. Г 65°
90° – 25° = 65°
Розв’язання
1) 36 : 4 = 9 (см) – сторона квадрата;
2) 9 • 9 = 81 (см2) – площа поля.
Відповідь: 81 см2.
Вправа 9 Запишіть 30 000 см3 у кубічних дециметрах. В 30 дм3
Вправа 10 Довжина ділянки прямокутної форми дорівнює 60 м, а площа — 720 м2. Знайдіть ширину ділянки. А 12 м
Розв’язання
720 : 60 = 12 (м) – ширина ділянки
Відповідь: 12 м.
Достатній рівень
Вправа 11
Перша сторона трикутника дорівнює 8 см, друга на 3 см довша за першу, але на 4 см коротша від третьої. Знайдіть периметр трикутника.
Розв’язання
1) 8 + 3 = 11 (см) – друга сторона трикутника;
2) 11 + 4 = 15 (см) – третя сторона трикутника;
2) 8 + 11 + 15 = 34 (см) – периметр трикутника.
Відповідь: 34 см.
Вправа 12 Накресліть прямокутник, площа якого дорівнює 24 см2, а одна зі сторін — 6 см. Знайдіть його периметр.
1) 24 : 6 = 4 (см) – друга сторона прямокутника.
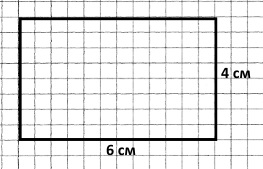
2) (6 + 4) • 2 = 20 (см) – периметр прямокутника.
Відповідь: 20 см.
Вправа 13 Промінь OM ділить розгорнутий кут АОВ на два кути так, що величина кута AOM утричі більша за величину кута MОВ. Знайдіть величину кута MOВ.
180 : 4 = 45° – величина кута МОВ.
Вправа 14 Ящик з вимірами 40 см, 30 см і 25 см заповнений піском. Знайдіть масу піску в ящику, якщо маса 1 дм3 піску дорівнює 1500 г.
Розв’язання
1) 40 • 30 • 25 = 30000 (см3) = 30 (дм3) – об'єм ящика;
2) 1500 • 30 = 45000 (г) = 45 (кг) – маса піску в ящику.
Відповідь: 45 кг.
Високий рівень
Вправа 15 Відрізок завдовжки 24 см поділили на три частини так, що довжина першої частини виявилась удвічі більшою за довжину другої, але на 4 см меншою від довжини третьої. Знайдіть довжину найкоротшої частини.
Розв’язання
2х + х + (2х + 4) = 24
5х + 4 = 24
5х = 20
х = 20 : 5
х = 4
Відповідь: 4 см.
Вправа 16 Периметр прямокутника дорівнює 28 см, а ширина на 4 см менша від довжини. Знайдіть площу прямокутника.
Розв’язання
(х + х – 4) • 2 = 28
2х – 4 = 14
2х = 18
х = 18 : 2
х = 9
9 – 4 = 5 (см) – ширина прямокутника.
9 • 5 = 45 (см2) – площа прямокутника.
Відповідь: 45 см2.
Вправа 17. Основою прямокутного паралелепіпеда є квадрат зі стороною 15 см, а сума довжин усіх ребер дорівнює 2 м. Знайдіть площу поверхні паралелепіпеда.
Розв’язання
2 м = 200 см
1) 15 • 8 = 120 (см) – сума довжин ребер основи;
2) 200 – 120 = 80 (см) – сума довжина ребер бічних граней;
3) 80 : 4 = 20 (см) – довжина бічного ребра;
4) 2 • (15 • 20 + 15 • 15 + 15 • 20) = 2 • (300 + 225 + 300) = 1650 (см2) – площа поверхні паралелепіпеда.
Відповідь: 1650 см2.
Вправа 18 В акваріумі, що має форму прямокутного паралелепіпеда завширшки 30 см і завдовжки 40 см, є вода. На скільки сантиметрів опуститься рівень води в акваріумі, якщо з нього забрати 12 л води?
Розв’язання
12 л = 12000 см3
1) 30 • 40 = 1200 (см2) – площа основи акваріума;
2) 12000 : 1200 = 10 (см)
Відповідь: рівень води в акваріумі опуститься на 10 см.