
Завдання 1096
До якого числа можна дописати справа 36, щоб дане число збільшилося в 103 рази?
Розв'язання
Нехай шукане число дорівнює а, то приписавши до нього справа 36, матимемо число а • 100 + 36. За умовою ця сума в 103 рази більша за а. Маємо рівняння:
100а + 36 = 103а
103а − 100а = 36
3а = 36
а = 36 : 3
а = 12
Відповідь: число 12.
Завдання 1097 Ознаки подільності чисел
Чи при кожному натуральному значенні n число 10n + 17 ділиться на 9? Так, бо сума усіх цифр даного числа дорівнює 9.
Завдання 1098
Заповни порожні клітинки стрічки, зображеної на малюнку, так, щоб сума чисел у кожних трьох сусідніх клітинках дорівнювала 10.
|
8
|
7
|
-5
|
8
|
7
|
-5
|
8
|
7
|
-5
|
8
|
7
|
-5
|
8
|
Завдання 1099 Ознаки подільності чисел
До числа 10 допиши зліва і справа по одній цифрі так, щоб утворене чотирицифрове число ділилося на 72.
Позначимо цифру, яку треба дописати, буквою а, за умовою число вигляду а10а має ділитися на 72, тому ділиться на 2, 3, 4, 6, 8, 9, бо 72 = 2 • 2 • 2 • 3 • 3. Отже, достатньо перевірити, щоб парне шукане число бути кратним 8 і 9.
Якщо цифра 2, то число 2102 не задовільняє умову, тому не підходить.
Якщо цифра 4, то число 4104 задовільняє умову, тому підходить.
Якщо цифра 6, то число 6106 не задовільняє умову, тому не підходить.
Якщо цифра 8, то число 8108 не задовільняє умову, тому не підходить.
Відповідь: треба дописали до числа 10 ліворуч і праворуч цифру 4.
Завдання 1100 Віднови цифри, замінені зірочками:
|
а) 1111 = ** • ***
б) 1265 = * • ** • *3
в) 1001 = * • *1 • **
г) 1166 = * • *3 • **
ґ) 2001 = * • *3 • **
|
а) 1111 = 11 • 101
б) 1265 = 5 • 11 • 23 або 1265 = 1 • 55 • 23
в) 1001 = 7 • 11 • 13 або 1001 = 1 • 11 • 91
г) 1166 = 2 • 53 • 11
ґ) 2001 = 3 • 23 • 29 або 2001 = 1 • 23 • 87
|
840|2 420|2 210|2 105|3 35|5 7|7 1| |
Завдання 1111
Знайди двоцифрове число, сума цифр якого дорівнює 14 і яке на 36 більше від числа, записаного тими самими цифрами в зворотному порядку. Оскільки сума цифр дорівнює 14, то цифрами шуканого числа можуть бути тільки: 7 і 7, 8 і 6 або 9 і 5. Перевірка показує, що задачу задовольняє тільки число 95. Перевірка: 95 – 59 = 36.
Завдання 1102
Батькові стільки років, скільки дочці та синові разом. Син удвоє старший за дочку і на 20 років молодший за батька. Скільки років кожному?
Розв'язання
Нехай дочці х років, тоді синові 3х років. Складаємо рівняння:
х + 2х = 2х + 20
х = 20 (р.) – років дочці;
2 • 20 = 40 (р.) – років синові;
40 + 20 = 60 (р.) – років батькові.
Відповідь: 20 років; 40 років; 80 років.
Завдання 1103
Перший рибалка дав для спільного обіду 2 окуні, другий — одного окуня, а третій — 600 грн. Як мали поділити між собою гроші два перші рибалки?
Міркуємо так. Усього 3 рибалки і 3 окуні. Кожен з них з'їв по 1 окуню, тобто другий рибалка з'їв свого окуня, перший рибалка з'їв свого окуня і віддав іншого окуня третьому рибалці, тому третій рибалка з'їв окуня, що упіймав перший рибалка, отже, третій рибалка має 600 грн віддати першому рибалці.
Завдання 1104
Скільки зайців та качок убив мисливець, якщо в кошику, куди він їх поклав, було 10 голів і 28 ніг?
Розв'язання
У зайців 4 лапи (ніг), а в качок 2 лапи (ніг).
1 спосіб
1) 10 • 4 = 40 (н.) – було б ніг, якби всі були зайцями;
2) 40 – 28 = 12 (н.) – "зайві" ноги, що належать качкам;
3) 4 – 2 = 2 (н.) – на стільки більше ніг у зайця, ніж у качки;
4) 12 : 2 = 6 (г.) – качок убив мисливець;
5) 10 – 6 = 4 (г.) – зайців убив мисливець.
2 спосіб
1) 10 • 2 = 20 (н.) – було б ніг, якби всі були качками;
2) 28 – 20 = 8 (н.) – "зайві" ноги, належать зайцям;
3) 4 – 2 = 2 (н.) – на стільки більше ніг у зайця, ніж у качки;
4) 8 : 2 = 4 (г.) – зайців убив мисливець;
5) 10 – 4 = 6 (г.) – качок убив мисливець.
Відповідь: 4 зайці і 6 качок.
Завдання 1105
Швидкість сокола більша за швидкість чайки на 75 км/год. Чайка літає швидше від стрижа в 1,5 раза. Знайди швидкість сокола, якщо вона більша за швидкість стрижа в 2 рази.
Розв'язання
Нехай швидкість стрижа х км/год, тоді швидкість сокола 2х км/год, а чайки — 1,5х км/год. Складаємо рівняння:
2х – 1,5х = 75
0,5х = 75
х = 75 : 0,5
х = 150 (км/год) – швидкість стрижа.
2х = 2 • 150 = 300 (км/год)
Відповідь: швидкість сокола 300 км/год.
Завдання 1106
Пасажир прийшов на вокзал за 5 хв до відходу електрички. Якби відстань до вокзалу була на 1 км більшою, то, йдучи з такою самою швидкістю, він запізнився б на 5 хв. З якою швидкістю йшов пасажир?
Розв'язання
1) 5 + 5 = 10 (хв) – час руху пасажира;
2) 1 : 10 = 0,1 (км/хв) – швидкість пасажира.
Відповідь: 0,1 км/хв.
Завдання 1107
З пункту A в пункт B кур’єр приніс посилку за 35 хв. Повертаючись в A, він більшив швидкість на 0,6 км/год, тому витратив на дорогу 30 хв. Чому дорівнює відстань між пунктами A і B?
Розв'язання
1 спосіб
0,6 км/год = 10 м/хв
Нехай вперед зв'язківець йішов зі швидкістю х м/хв, а назад — зі швидкістю (х + 10) м/хв. Складаємо рівняння:
35х = 30(х + 10)
35х = 30х + 300
35х – 30х = 300
5х = 300
х = 300 : 5
х = 60 (км/хв) – швидкість пасажира;
60 м/хв • 35 хв = 2100 м = 2,1 км.
2 спосіб
0,6 км/год = 10 м/хв. Нехай швидкість зв'язківця х м/хв. Складаємо рівняння:
х/30 – х/35 = 10
35/1050 х – 30/1050 х = 10
5/1050 х = 10
х = 10 : 5/1050
х = 10/1 • 1050/5
х = 2100
Відповідь: 2100 м, або 2,1 км.
Завдання 1108
Електричка пройшла повз мене за 5 c, а повз платформу завдовжки 150 м — за 15 с. З якою швидкістю їхала електричка?
Розв'язання
Відстань, яка дорівнює довжині електрички, вона здолала за 5 с, а відстань 150 м — за 10 с.
1) 15 – 5 = 10 (с) – час руху електрички;
2) 150 : 10 = 15 (м/с) – швидкість електрички.
Відповідь: 15 м/с.
Завдання 1109
Через 2 роки хлопчик буде вдвоє старшим, ніж був 2 роки тому. А дівчинка через 3 роки буде в 3 рази старшою, ніж була 3 роки тому. Хто з них старший?
Розв'язання
Розв'язання
Нехай тепер хлопчикові х років, тоді 2 роки тому йому було (х–2) роки, а через 2 роки буде — (х+2). Складаємо рівняння.
х + 2 = 2(х – 2)
х + 2 = 2х – 4
2х – х = 2 + 4
х = 6 (р.) – вік хлопчика.
Якщо дівчинці тепер у років, то 3 роки тому їй було (у–3), а через 3 роки буде (у + 3). Складаємо рівняння:
у + 3 = 3(y – 3)
у + 3 = 3у – 9
3у – у = 3 + 9
2у = 12
у = 12 : 2
у = 6 (р) – вік дівчинки.
Відповідь: їхній вік однаковий, бо кожному 6 років.
Завдання 1110
Маса повної каністри з водою дорівнює 23 кг, а заповненої наполовину — 12,5 кг. Яка маса порожньої каністри?
Розв'язання
1) 23 − 12,5 = 10,5 (кг) − маса половини молока;
2) 12,5 − 10,5 = 2 (кг) − маса порожньої каністри.
Відповідь: 2 кг.
Завдання 1111
20 туристів — чоловіки, жінки та діти — разом несли вантаж 200 кг. Скільки серед них було дітей, якщо кожний чоловік ніс 20 кг, кожна жінка — 5 кг, а кожна дитина — 3 кг?
Розв'язання
Нехай було x чоловіків, y жінок і k дітей, тоді x + у + k = 20 (1).
Разом несли вантажу: 20х + 5у + 3k = 200, звідси
20x/5 + 5y/5 + 3k/5 = 200/5 або 4х + у + 3k/5 = 40 (2).
Число k повинно ділитися на 5.
Якщо k = 5, тоді, підставляючи в рівняння (1) і (2), маємо:
x + у + 5 = 20, звідси х + у = 15
4х + у + 3 = 40, звідки 4x + y = 37
Не існує пари натуральних чисел, що задовільняє ці рівняння одночасно.
Якщо k = 10, тоді, підставляючи в рівняння (1) і (2), маємо:
x + у + 10 = 20, звідси х + у = 10
4х + у + 6 = 40, звідки 4x + y = 34
Розв'язки рівнянь: х = 8 і у = 2.
Відповідь: 10 дітей.
Завдання 1112
Одне з двох чисел закінчується нулем. Якщо цей нуль закреслити, то вийде друге число. Знайди ці числа, якщо їх сума дорівнює 924.
Розв'язання
Нехай друге число х, тоді перше число 10х, а їхня сума 11х. Складаємо рівняння.
х + 10х = 924
11х = 924
х = 924 : 11
х = 84 – друге число;
84 • 10 = 840 – перше число.
Відповідь: 840 і 84.
Завдання 1113
Числа 1, 2, 3, 4, 5, 6, 7, 8 і 9 розмісти у кругах так, щоб сума чисел на кожній стороні дорівнювала 17.
2 9 5 1
8 6
4 7
3
Завдання 1114
Познач у зошиті 9 точок, як зображено на малюнку. Не відриваючи олівця від паперу, проведи 4 відрізки так, щоб вони пройшли через усі 9 точок.
Завдання 1115
З 9 монет одна фальшива (легша за інші). Як виявити фальшиву монету двома зважуваннями на шалькових терезах?
Міркуємо так. Треба всі 9 монет порівну розкласти на 3 купки. Якщо якась із двох таких купок виявиться легшою, то фальшива монета в тій купці. Якщо ж вони є в рівновазі, то фальшива монета в треті купці. Так в результаті першого зважування, можна відкинути 6 монет. Далі зважуємо будь-які дві монети із залишених. Якщо якась із них легша — вона фальшива. Якщо дві ці монети врівноважуються, то фальшивою є третя.
Завдання 1116
Андрій, Борис, Віра і Ганна розмістили свої пости з математичним проєктом в соціальній мережі. Найбільше від усіх лайків отримав пост Ганни, пост Віри — не менше, ніж пост Бориса. Чи правда, що пости дівчат отримали більше лайків, ніж пости хлопців? Так, бо в порядку спадання кількості постів діти розташувалися так: Ганна, Віра, Борис. Пост Андрій може бути після поста Бориса.
Г + В > Б + А
Завдання 1117
Скількома способами можна розмістити трьох гостей на трьох стільцях? 6 способів.
1 • 2 • 3 = 6
Завдання 1118
Скільки різних трицифрових чисел можна утворити із цифр 1, 2 і 3 так, щоб цифри не повторювалися? Шість (123; 132; 213; 231; 312; 321)
Завдання 1119
В автомобілі 4 вільні місця. Скількома способами можуть розміститися на них 4 пасажири? 24 способи.
1 спосіб
1) 1, 2, 3, 4
2) 1, 2, 4, 3
3) 1, 3, 2, 4
4) 1, 3, 4, 2
5) 1, 4, 2, 3
6) 1, 4, 3, 2
по 6 способів 4 рази, тому 6 • 4 = 24 способи.
2 спосіб
1 • 2 • 3 • 4 = 24
Завдання 1120
Кожна з п’яти подруг написала одне повідомлення кожній іншій. Скільки всього повідомлень вони написали? 20 повідомлень.
4 • 5 = 20
Завдання 1221
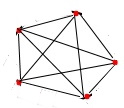
На класній дошці позначили 5 точок і кожну з них сполучили відрізком з кожною іншою. Скільки утворилося відрізків? Десять.
4 + 3 + 2 + 1 = 10
Завдання 1122
Скількома способами можна нанизати на нитку 6 різних намистин? 36 способів
1, 2, 3, 4, 5, 6
2, 1, 3, 4, 5, 6
2, 3, 1, 4, 5, 6
2, 3, 4, 1, 5, 6
2, 3, 4, 5, 1, 6
2, 3, 4, 5, 6, 1
по 6 способів для 6 намистин, тому 6 • 6 = 36 способів.
Скількома способами можна нанизати на нитку 7 різних намистин? 49 способів
1, 2, 3, 4, 5, 6, 7
2, 1, 3, 4, 5, 6, 7
2, 3, 1, 4, 5, 6, 7
2, 3, 4, 1, 5, 6, 7
2, 3, 4, 5, 1, 6, 7
2, 3, 4, 5, 6, 1, 7
2, 3, 4, 5, 6, 7, 1
по 7 способів для 7 намистин, тому 7 • 7 = 49 способів.
Завдання 1123
Котра тепер година, якщо до закінчення доби залишилася п’ята частина часу, який пройшов від її початку?
Розв'язання
Нехай до закінчення доби залишилося х год, а від її початку минуло (24 - х) год. Складаємо рівняння:
5х = 24 – х
6х = 24
х = 24 : 6
х = 4
24 – 4 = 20 (год)
Відповідь: тепер 20 год.
Завдання 1124
Стародавня задача. Селянин купував на ярмарку коня, корову і вівцю. За коня він віддав 5/8 усіх своїх грошей, за корову — половину того, що дав за коня, за вівцю — останніх 5 карбованців. Скільки коштували кінь і корова?
Розв'язання
Нехай у селянина було х грн, тоді дав за коня 5/8х грн, а за корову 5/16х грн. Складаємо рівняння.
5/8х + 5/16х + 5 = х
16/16х – 10/16х – 5/16х = 5
1/16х = 5
х = 5 : 1/16
х = 5 • 16/1
х = 80
80 • 5/8 = 50 (грн) – заплатив за коня;
80 • 5/16 = 25 (грн) – заплатив за корову.
Відповідь: 50 грн і 25 грн.
Завдання 1125 Найменше спільне кратне
Андрій ходить до бібліотеки раз на 3 дні, Борис — раз на 4 дні, Віктор — раз на 5 днів. Утрьох вони зустрілися в бібліотеці в суботу. Коли наступного разу всі вони знову зустрінуться в бібліотеці?
Розв'язання
Після суботи до наступної зустрічі усіх трьох хлопців мало пройти число днів, кратне числам 3, 4 і 5.
НСК(3;4;5) = 2 • 2 • 3 • 5 = 60
60 : 7 = 8 (ост. 4). Отже, до першої зустрічі має пройти 8 тижнів і 4 дні. Четвертий день після суботи — середа.
Відповідь: у середу.
Завдання 1126
Якщо на одну шальку терезів покласти шматок сала, а на другу — 3/4 такого самого шматка сала і гирі на 3/4 кг, то терези врівноважаться. Знайди масу шматка сала.
Розв'язання
1 спосіб
1) 1 – 3/4 = 1/4 – становить гиря масою 3/4 кг;
2) 3/4 : 1/4 = 3/4 • 4 = 3(кг) – маса шматка сала.
2 спосіб
Нехай маса сала х кг, тоді на другій шальці кладемо 3/4х кг сала. Складаємо рівняння:
3/4х + 3/4 = х
х – 3/4х = 3/4
1/4х = 3/4
х = 3/4 : 1/4
х = 3/4 • 4/1
х = 3
Відповідь: 3 кг.
Завдання 1127
Пішов мисливець на полювання з собакою. Йдуть вони лісом, і раптом собака побачив зайця. Відстань від собаки до зайця дорівнює 40 стрибкам собаки, а відстань, яку собака пробігає за 5 стрибків, заєць пробігає за 6 стрибків. За скільки стрибків собака наздожене зайця? (Стрибки роблять одночасно і собака, і заєць.)
Розв'язання
1) 6 − 5 = 1 (стрибок) − на стільки наближаються щоразу.
2) Щоразу за 6 стрибків собака наблизиться на відстань, що дорівнює своєму одному стрибку, тому наздожене зайця.
40 • 6 = 240 (стрибків)
Відповідь: за 240 стрибків.
Завдання 1128
Собака доганяє зайця, який знаходиться від нього за 150 футів. Він стрибає на 9 футів кожного разу, коли заєць стрибає на 7 футів. Скільки разів має стрибнути собака, щоб наздогнати зайця?
Розв'язання
1) 9 − 7 = 2 (ф.) − на стільки наближаються за 1 стрибок.
2) 150 : 2 = 75 (р.)
Відповідь: собака має стрибнути 75 разів.
Завдання 1129
Є шестилітрова банка олії та дві порожні банки: трилітрова і чотирилітрова. Як налити 1 літр олії в трилітрову банку?
З шестилітрової банки олію наливаємо в 4-х літрову банку, а з неї виливаємо в 3-х літрову. Потім виливаємо з 3-х літрової банки олію в шестилітрову банку, а з 4-х літрової переливаємо у 3-х літрову банку 1 л води.