
Завдання 202
У першій таблиці величини пропорційні, у другій таблиці — ні.
Завдання 203 Прямо пропорційні величини
а) маса товару і його вартість; Так
б) довжина дроту і його маса; Так
в) маса тіла і його об’єм; Так
г) довжина ребра куба і його об’єм; Ні
ґ) периметр квадрата і довжина його сторони. Так
д) площа квадрата і довжина його сторони. Ні
Завдання 204
Приклади. Кількість і вартість товару.
Завдання 205 Обернено пропорційні величини
А Кількість цукерок і їх ціна; Ні
Б Кількість роботів і час виконання ними роботи; Так
В Кількість спідниць і кількість витраченої на них тканини; Ні
Г Швидкість і час на заданій ділянці. Так
Завдання 206
Автомобіль проїхав 240 км. За скільки годин він проїде цю відстань, якщо його швидкість:
10 км/год: 240 : 10 = 24 (год)
20 км/год: 240 : 20 = 12 (год)
30 км/год: 240 : 30 = 8 (год)
40 км/год: 240 : 40 = 6 (год)
60 км/год: 240 : 60 = 4 (год)
80 км/год: 240 : 80 = 3 (год)
Завдання 207
10 зошитів коштують 120 грн.Скільки коштують 2, 3, 4, 5, 9, 30, 50 таких зошитів?
120 : 10 = 12 (грн) – ціна зошита;
12 • 2 = 24 (грн) – коштують 2 зошита;
12 • 3 = 36 (грн) – коштують 2 зошита;
12 • 4 = 28 (грн) – коштують 2 зошита;
12 • 5 = 60 (грн) – коштують 2 зошита;
12 • 9 = 108 (грн) – коштують 2 зошита;
12 • 30 = 360 (грн) – коштують 2 зошита;
12 • 50 = 600 (грн) – коштують 2 зошита.
Завдання 208
Мідний дріт довжиною 20 м важить 1 кг. Скільки важать 40 м такого дроту?
Мідний дріт довжиною 20 м важить 1 кг. Яка довжина дроту масою 2 кг?
Мідний дріт довжиною 40 м важить 2 кг. Скільки важать 20 м такого дроту?
Мідний дріт довжиною 40 м важить 2 кг. Яка довжина дроту масою 1 кг?
Завдання 209
За деякий час автобус проїхав 160 км. Яку відстань за цей час він проїде, якщо рухатиметься зі швидкістю:
а) у 2 рази більшою; У 2 рази більшу, тобто 160 • 2 = 320 (км)
б) у 2 рази мешою? У 2 рази меншу, тобто 160 : 2 = 80 (км)
Завдання 210
На пошиття певної кількості костюмів пішло 250 м тканини. Скільки тканини піде на пошиття костюмів, якщо їх кількість:
а) у 2 рази менша, У два рази менше, тобто 250 : 2 = 125 (м)
б) у 3 раз більша? У три рази більше, тобто 250 • 3 = 750 (м)
Завдання 211
|
Довжина тканини, м
|
8
|
16
|
4
|
5
|
7
|
10
|
|
Вартість, грн
|
600
|
1200
|
300
|
375 | 525 | 750 |
Завдання 212
Установи кількість сторінок в одному блокноті. Скільки сторінок в 4 і 5 таких блокнотах.
1 блокнот — 50 сторінок
4 блокноти — 175 сторінок
5 блокнотів — 200 сторінок
Завдання 213
|
Об'єм, л
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
Маса, кг
|
0,8
|
1,6 |
2,4
|
3,2
|
4 | 4,8 | 5,6 |
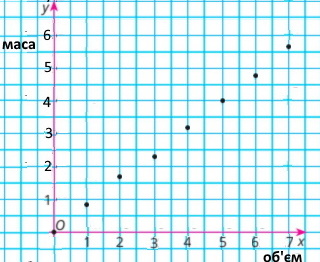
Завдання 214
3 0,5 т руди можна виплавити 0,3 т чавуну.
1 : 0,5 • 0,3 = 0,6 (т) – чавуну можна виплавити з 1 т руди.
2 : 0,5 • 0,3 = 1,2 (т) – чавуну можна виплавити з 2 т руди.
3 : 0,5 • 0,3 = 1,8 (т) – чавуну можна виплавити з 3 т руди.
10 : 0,5 • 0,3 = 6 (т) – чавуну можна виплавити з 10 т руди.

Завдання 215
Маса 2 м3 дров дорівнює 1600 кг. Знайди масу 112 кубометрів таких дров.
Розв'язання
2 м3 — 1600 кг
112 м3 — х кг
2/112 = 1600/х; х = 1600 • 112 : 2 = 89600 (кг)
Відповідь: 89600 кг.
Завдання 216
Із 10 кг жита виходить 9 кг борошна. Скільки треба змолотити жита, щоб отримати 900 кг борошна?
Розв'язання
10 кг — 9 кг
х кг — 900 кг
10/х = 9/900; х = 900 • 10 : 9 = 1000 (кг)
Відповідь: 1000 кг.
Завдання 217
За малюнком знайдіть вартість кожної з упаковок з однаковими пиріжками.
Розв'язання
4 шт. — 136 грн
х шт. — 272 грн
4/х = 136/272; х = 4 • 272 : 136 = 8 (п.) – пиріжків у другому пакунку;
4 шт. — 136 грн
12 шт. — х грн
4/12 = 136/х; х = 136 • 12 : 4 = 408 (грн) – вартість третього пакунка;
4 шт. — 136 грн
6 шт. — х грн
4/6 = 136/х; х = 136 • 6 : 4 = 204 (грн) – вартість четвертого пакунка;
4 шт. — 136 грн
х шт. — 340 грн
4/х = 136/340; х = 340 • 4 : 136 = 10 (п.) – пиріжків у п'ятому пакунку.
Завдання 218
Велосипедистка за 0,3 год проїхала 4,2 км. Скільки кілометрів вона проїде за 2 год, рухаючись з такою ж швидкістю?
Розв'язання
0,3 год — 4,2 км
2 год — х км
0,3/2 = 4,2/х; х = 4,2 • 2 : 0,3 = 28 (кг)
Відповідь: 28 кг.
Завдання 219
Із 100 кг свіжих яблук можна отримати 5,8 кг сушених. Скільки сушених яблук вийде із 750 кг свіжих?
Розв'язання
100 кг — 5,8 кг
750 кг — х км
100/750 = 5,8/х; х = 750 • 5,8 : 100 = 43,5 (кг)
Відповідь: 43,5 кг.
Завдання 220
Скільки треба взяти картоплі, щоб отримати 90 кг крохмалю, якщо з 30 кг картоплі виходить 5,4 кг крохмалю?
Розв'язання
30 кг — 5,4 кг
х кг — 90 км
30/х = 5,4/90; х = 30 • 90 : 5,4 = 500 (кг)
Відповідь: 500 кг.
Завдання 221
Заробітну плату Сашку нараховують за кількістю годин, які він відпрацював. В минулому місяці Сашко відпрацював 180 год і отримав 32 400 грн. Скільки грошей має він отримати в цьому місяці, якщо відпрацював 188 год?
Розв'язання
180 год — 32400 грн
188 год — х грн
180/188 = 32400/х; х = 188 • 32400 : 180 = 33840 (кг)
Відповідь: 33840 кг.
Завдання 222
Чи пропорційна площа квадрата довжині його сторони?
Розв'язання
a — s
2a — х
a/2a = s/х; х = 2a • s : a = 2s
Відповідь: так, пропорційна.
Завдання 223
За місяць 2 бригади можуть звести 4 поверхи будинку. Як зміниться термін зведення цих 4 поверхів, якщо:
а) кількість бригад зросте у 3 рази; Зменшиться у 3 рази
б) кількість бригад зменшиться у 2 рази. Збільшиться у 2 рази
Завдання 224
На пошиття 16 спідниць є 20 м тканини. Як зміниться кількість спідниць, що можна пошити з цієї тканини, якщо на одну спідницю витрачати:
а) у 5 разів менше тканини; Збільшиться у 5 разів
б) у 2 рази більше тканини? Зменшиться у 2 рази
Завдання 225
|
Швидкість, км/год
|
20
|
80
|
40
|
80
|
|
Час, год
|
24
|
6
|
12
|
6 |
Завдання 226
Олена хоче купити 4 альбоми за ціною 180 грн. Скільки альбомів вона зможе купити за ці ж гроші, якщо ціна альбому стане 90 грн?
Розв'язання
4 альб. — 180 грн
х альб. — 90 грн
4/х = 180/90; х = 90 • 4 : 180 = 2 (альб.)
Відповідь: 2 альбоми.
Завдання 227
За 24 хв насос викачує 144 м3 води. За який час три насоси викачають цей об’єм води?
Розв'язання
1 н. — 24 хв
3 н. — х хв
1/3 = х/24; х = 24 • 1 : 3 = 8 (хв)
Відповідь: за 8 хвилини.
Завдання 228
З 20 кг морської води можна добути 0,5 кг солі. Скільки потрібно взяти морської води, щоб отримати 45 кг солі? Скільки солі можна добути з 1300 кг морської води?
Розв'язання
20 кг — 0,5 кг
х кг — 45 кг
20/х = 0,5/45; х = 20 • 45 : 0,5 = 1800 (кг)
20 кг — 0,5 кг
1300 кг — х кг
20/1300 = 0,5/х; х = 1300 • 0,5 : 20 = 32,5 (кг)
Відповідь: 1800 кг; 32,5 кг.
Завдання 229
Маса 0,25 дм3 бронзи дорівнює 2,2 кг. Знайдіть:
а) масу 2 м3 бронзи;
Розв'язання
0,25 дм3 — 2,2 кг
2000 дм3 — х кг
0,25/2000 = 2,2/х; х = 2,2 • 2000 : 0,25 = 17600 (кг)
Відповідь: 17600 кг.
б) об’єм бронзової деталі, якщо її маса 4,4 кг.
Розв'язання
0,25 дм3 — 2,2 кг
х дм3 — 4,4 кг
0,25/х = 2,2/4,4; х = 4,4 • 0,25 : 2,2 = 0,5 (дм3)
Відповідь: 0,5 дм3.
Завдання 230
Три робітниці можуть виконати замовлення за 8 днів. За скільки днів можуть виконати це замовлення 4 робітниці?
Розв'язання
3 р. — 8 дн.
4 р. — х дн.
3/4 = х/8; х = 8 • 3 : 4 = 6 (дн.)
Відповідь: 6 днів.
Завдання 231
Двоє робітників виконують деяке замовлення за 12 днів. Скільки ще потрібно робітників, щоб виконати це замовлення за 8 днів, якщо продуктивність праці залишиться незмінною?
Розв'язання
2 р. — 12 дн.
х р. — 8 дн.
2/х = 8/12; х = 12 • 2 : 8 = 3 (р.) – виконають замовлення за 8 днів;
3 – 2 = 1 (р.) – потрібно робітників.
Відповідь: 1 робітник.
Завдання 232
За 3 год Ганна пройшла 16 км. За який час вона пройде 30 км, рухаючись із такою самою швидкістю? Скільки кілометрів вона пройде за 5 год? Округли до десятих.
Розв'язання
3 год — 16 км
х год — 30 км
3/х = 16/30; х = 30 • 3 : 16 = 5,625 (год) ≈ 5,6(год)
3 год — 16 км
5 год — х км
3/5 = 16/х; х = 16 • 5 : 3 = 26,7 (км)
Відповідь: 26,7 км.
Завдання 233
Велосипедист, рухаючись зі швидкістю 12 км/год, на шлях від міста до села витратив 5 год. З якою швидкістю він має рухатись, щоб проїхати цю відстань за 4 год?
Розв'язання
5 год — 12 км/год
4 год — х км/год
5/4 = х/12; х = 12 • 5 : 4 = 15 (км/год)
Відповідь: 15 км/год.
Завдання 234
Туристки йшли до бази відпочинку 5 год зі швидкістю 4 км/год, а поверталися назад на велосипедах зі швидкістю 10 км/год. Скільки часу вони витратили на зворотній шлях?
Розв'язання
5 год — 4 км/год
х год — 10 км/год
5/х = 10/4; х = 5 • 4 : 10 = 2 (год)
Відповідь: 2 год.
Завдання 235
Для фарбування 7,5 м² підлоги потрібно 0,75 кг фарби. Скільки фарби потрібно, щоб пофарбувати підлогу, розміри якої 3,5 м і 4,2 м?
Розв'язання
1) 3,5 • 4,2 = 14,7 (м²) – площа підлоги;
2) 7,5 м² — 0,75 кг
14,7 м² — х кг
7,5/14,7 = 0,75/х; х = 14,7 • 0,75 : 7,5 = 1,47 (кг)
Відповідь: 1,47 кг.
Завдання 236
На фарбування 20 м² стіни потрібно 2,5 кг штукатурки. Скільки штукатурки потрібно, щоб пофарбувати коридор, загальна довжина стін якого 13,6 м, а висота 2,5 м?
Розв'язання
1) 13,6 • 2,5 = 34 (м²) – загальна площа стін.
2) 20 м² — 2,5 кг
34 м² — х кг
20/34 = 2,5/х; х = 2,5 • 34 : 20 = 4,25 (кг)
Відповідь: 4,25 кг.
Завдання 237
Маса 3 м3 льоду дорівнює 2,7 т. Знайди масу льодяного куба (у кг), якщо його ребро дорівнює 0,5 м.
Розв'язання
1) 0,5 • 0,5 • 0,5 = 0,125 (м3) – об'єм куба.
2) 3 м3 — 2,7 т
0,125 м3 — х т
3/0,125 = 2,7/х; х = 2,7 • 0,125 : 3 = 0,1125 (т) = 112,5 (кг)
Відповідь: 112,5 т.
Завдання 238
Щоб отримати 60 кг мельхіору, треба сплавити 9 кг нікелю, 12 кг цинку, решту — міді. Скільки кілограмів кожного з цих металів треба взяти, щоб отримати 100 кг мельхіору?
Розв'язання
1) 60 кг — 9 кг
100 кг — х кг
60/100 = 9/х; х = 9 • 100 : 60 = 15 (кг) – потрібно нікелю;
2) 60 кг — 12 кг
100 кг — х кг
60/100 = 12/х; х = 12 • 100 : 60 = 20 (кг) – потрібно цинку;
3) 100 – (15 + 20) = 100 – 35 = 65 (кг) – потрібно міді.
Відповідь: 15 кг; 20 кг; 65 кг.
Завдання 239
Щоб отримати 0,5 кг латуні, потрібно сплавити 300 г міді і 200 г цинку. Скільки кілограмів кожного з металів треба взяти, щоб отримати 70 кг латуні?
1) 0,5 кг — 300 кг
70 кг — х кг
0,5/70 = 300/х; х = 70 • 300 : 0,5 = 42000 (г) = 42 (кг) – потрібно міді;
2) 0,5 кг — 200 кг
70 кг — х кг
0,5/70 = 200/х; х = 70 • 200 : 0,5 = 28000 (кг) = 28 (кг) – потрібно цинку.
Відповідь: 42 кг; 28 кг.
Завдання 240
Зроби необхідні вимірювання та обчисли периметр і площу цієї деталі за кресленням.
Завдання 241 Покажи на прикладах, що завжди:
а) якщо a/b = c/d, то (a + b)/b = (c + d)/d
15/3 = 45/9 (5 = 5), 15/3 + 3/3 = 45/9 + 9/9, (15 + 3)/3 = (45 + 9)/9 (6 = 6)
б) якщо a/b = c/d, то a/с = (a + b)/(c + d)
15/3 = 45/9 (5 = 5), 15/45 = (15+3)/(45+9) (15/45 = 18/54, 3/9 = 3/9)
Вправи для повторення
Завдання 242 Рівняння
|
а) 5,2x – 3,8 = 14
5,2x = 14 + 3,8
5,2x = 17,8
х = 17 8/10 : 5 2/10
х = 17 4/5 : 5 1/5
х = 89/5 : 26/5
х = 89/5 • 5/26
х = 89/26
х = 3 11/26
|
б) 3,9 – 1,2x = 0,3
1,2x = 3,9 – 0,3
1,2x = 3,6
х = 3,6 : 1,2
х = 3
|
Завдання 243
Сума кутів трикутника більша від одного з них на 150° і від другого – на 75°. Знайди міру третього кута трикутника.
Розв'язання
1) 180° – 150° = 30° – перший кут;
2) 180° – 75° = 105° – другий кут;
3) 180° – (30° + 105°) = 180° – 135° = 45° – третій кут.
Відповідь: 30°, 105°, 45°.
Завдання 244 Вирази
Якщо x = y = –4, 36x + 64y = 36 • (–4) + 64 • (–4) = –4 • (36 + 64) = –4 • 100 = –400