1) на осі абсцис лежать точки: E і G;
на осі ординат лежать точки: F і H;
2) координати всіх зображених точок: E(–3;0), A(–3;2), F(0;3), G(2;0), B(3;4), C(4;–2), D(–2;–2), H(0;–3)
3) абсциси точок А, F, H, С: –3, 0, 0, 4
4) ординати точок С, D, E, А: –2, –2, 0, 2
5) чверті, у яких лежать точки B, A, D, C: I, II, III, IV
Завдання 1378
|
Точка
|
Абсциса
|
Ордината
|
Чверть
|
|
K(4;–9)
L(–15; –10)
M(1,4; 0,5)
N(–1/4;3/5)
|
4
–15
1,4
–1/4
|
–9
–10
0,5
3/5
|
IV
II
I
II
|
Завдання 1379
A(–3;2,5), E(–2,5;0), B(0;3), C(1;2,5), F(2,5;0), D(3;2), Z(3;–3), G(0;–1,5), X(–1;–2), Y(–3;–3)
Завдання 1380
A(–3;2), F(–2;0), B(–1;2), C(0;2), G(1,5;0), E(2;1), D(2;3), M(2;–1), L(0;–2), K(–2;–3)
Завдання 1381
A(–4;4), B(4;4), C(4;–4), D(–4;–4), N(6;7), M(–2;7), K(6;–1)
Завдання 1382
1) лежать на осі абсцис точки з координатами: (–2;0), (1;0), (5;0)
2) лежать на осі ординат точки з координатами: (0;–2), (0;1), (0;5)
3) мають ординату 3 точки з координатами: (–4;3), (0;3), (7;3)
4) мають абсцису –2 точки з координатами: (–2;–5), (–2;0), (–2;11)
Завдання 1383
Координати чотирьох точок, які лежать у різних координатних чвертях:
(5;5), (–5;5), (–5;–5), (5;–5)
Завдання 1384
Табір туристів розташований у точці О, стороні однієї клітинки відповідає відстань 1 км. Знайдіть координати місця, у яке прийдуть туристи, вийшовши з табору та пройшовши:
1) 4 км на захід і 3 км на південь: (–4;–3)
2) 3 км на схід і 5 км на північ: (–1;–2)
3) 2 км на захід і 4 км на північ: (–3;–6)
4) 2 км на схід: (–1;–6)
Завдання 1385, 1386
 |
 |
Завдання 1387, 1388
 |
 |
Завдання 1389
Цей чотирикутник називається прямокутник.

Завдання 1390, 1391, 1392
 |
 |
 |
Завдання 1393, 1394
 1) перетину з осями координат:
С(0;2) i D(2;0)
2) абсциса дорівнює –1: E(–1;3)
3) ордината дорівнює –2: F(4;–2)
|
 1) перетину з осями координат:
A(–2;0) i B(0;1)
2) абсциса дорівнює 4: F(4;3)
3) ордината дорівнює –2: E(–6;–2)
|
Завдання 1395
Через точку В проведіть пряму, паралельну прямій АС, а через точку А — пряму, перпендикулярну до прямої ВС.

Завдання 1396, 1397
 |
 |
Завдання 1398
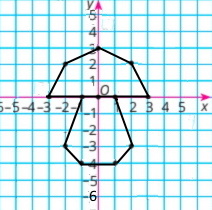
Усі точки лежать на колі.
Завдання 1399, 1400
 2) Координати точки N(3;–2)
3) (4,5 + 3) • 2 = 15 (см) – периметр;
4,5 • 3 = 13,5 (см²) – площа.
|
 2) Координати точок C(–1;3) і D(3;3)
3) 4 • 4 = 16 (см) – периметр;
4 • 4 = 16 (см²) – площа.
|
Завдання 1401
Зобразіть на координатній площині всі точки (x; y), для яких:
|
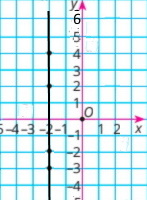
1) x = –2; y — довільне;
 |
3) |x| ≤ 1; y ≥ 0;
 |
|
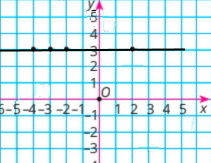
2) x — довільне; 1 ≤ y ≤ 3;
 |
4) –2 ≤ x ≤ 3; |y| ≤ 1.
|
Завдання 1402
Зобразіть на координатній площині всі точки (x; y), для яких:
|
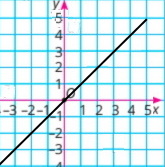
1) x — довільне; y = 3;
 |
2) |x| ≤ 1; |y| ≤ 2.
|
Завдання 1403 Ознаки подільності числа
У записі натурального числа n переставили деякі цифри й одержали число, утричі менше від n. Обґрунтуйте, що число n ділиться на 9. Одержане число утричі менше, а сума цифр числа однакова, тому число n ділиться на 3, а, отже, воно ділиться й на 9.
Завдання 1404
1) 1,2 – 9/20 = 1,2 – 0,45 = 0,75
2) –3 2/7 + 1 9/14 : 0,5 = –3 2/7 + 23/14 : 1/2 = –3 2/7 + 23/7 = –3 2/7 + 3 2/7 = 0
3) 4,15 – (2 1/2 – 1 3/4) = 4,15 – (2,5 – 1,75) = 4,15 – 0,75 = 3,4
Завдання 1405 Рівняння
|
1) 2(y – 4) = y
2у – у = 8
у = 8
|
2) 3(z + 1) = 5(z – 5)
3z – 5z = –25 – 3
–2z = –28
z = 14
|
3) 2/7 (2х – 1) = 6
2x – 1 = 6 : 2/7
2x – 1 = 21
2x = 22
x = 11
|
Завдання 1406
Автомобіль має перевезти вантаж з міста А до міста В, відстань між якими 180 км. Водій автомобіля планував їхати 3 год й о 10 годині ранку бути в місті В. Однак він виїхав із запізненням і, щоб прибути до міста В вчасно, збільшив заплановану швидкість на 20%. О котрій годині автомобіль виїхав з міста А?
Розв'язання
1) 180 : 3 = 60 (км/год) – запланована швидкість;
2) 60 + 60 • 0,2 = 72 (км/год) – збільшена швидкість;
3) 180 : 72 = 2,5 (год) – час в дорозі;
4) 10 год – 2,5 год = 7,5 год = 7 год 30 хв – час виїзду з міста А.
Відповідь: о 7 год 30 хв ранку.
Завдання 1407
Скільки грамів солі потрібно додати до 160 г води, щоб одержати 20-відсотковий розчин солі?
Розв'язання
160 г — 80%
х г — 20%
160/x = 80/20; х = 160 • 20 : 80; х = 40 (г)
Відповідь: потрібно 40 г солі.


