Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

Розв’язуємо усно

Завдання 1 Збільште суму чисел 24 и 18 на 36.

(24 + 18) + 36 = (24 + 36) + 18 = 60 + 18 = 78

 

Завдання 2 Подвойте суму чисел 418 и 232.

(418 + 232) • 2 = 650 • 2 = (600 + 50) • 2 = 1200 + 100 = 1300

 

Завдання 3 Знайдіть третину від суми чисел 103 і 47.

(103 + 47) : 3 = 150 : 3 = 50

 

Завдання 4

З автобуса на зупинці вийшло 15 пасажирів. Дев’ятеро з них пішли до пішохідного переходу, а решта людей почали переходити дорогу, обходячи автобус спереду. Скільки людей вчинили неправильно?

Розв’язання

15 – 9 = 6 (л.) – люди, що вчинили неправильно.

Відповідь: 6 людей. 

 

Завдання 5 У коробці лежать сині та зелені олівці. Зелених олівців є 19, що на 17 менше, ніж синіх. Скільки олівців лежить у коробці?

Розв'язання

1) 19 + 17 = 36 (шт.) ‒ синіх олівців у коробці.

2) 19 + 36 = 55 (шт.) ‒ всього олівців у коробці.

Відповідь: у коробці лежить 55 олівців.

 

Завдання 6 Є два відра місткістю 9 л і 4 л. Як, користуючись ними, можна налити в діжку 6 л води?

Розв'язання

9 ‒ 4 ‒ 4 + 9 ‒ 4 = 1 + 5 = 6 (л.)

Налити в діжку 9 л води, забрати з діжки 2 рази по 4 л води, налити 9 л води, забрати з діжки 4 л води або набрати 9 л води у відро і відлити 2 рази по 4 л у інше відро, отриману 1 л налити у діжку, потім набрати 9 л води і відлити 4 л води у інше відро, отримані 5 л води налити в діжку.

 

Вправи

Вправа 212 Письмове віднімання

1) _27146      24317       2829	2) _ 56789        9876       46913	3) _524278      344929      179349
4) _46000185       8123456      37876729	5) _72430034      23082408      49347626	8) _1000000000        637891452        362108548

Вправа 213 

_60015    7428  52587

_372894   216156   156738

_38020301  18479563  19540738

_537866285   496707539    41158746

Вправа 214 

_82314    8425  73889

Перевірка: +73889    8425  82314

_24000203    4091574   19908629

Перевірка: +19908629    4091574  24000203

Вправа 215 

_46002  28396  17606

Перевірка: +17606   28396   46002

_251762    28187   223575

Перевірка: +223575    28187   251762

Вправа 216 На скільки:

1) число 4328 менше від числа 21 514;

2) число 258 143 більше за число 164 275?

Розв'язання

1) _ 21514        4328       17186

2) _ 258143       164275         93868

Вправа 217 На скільки:

1) число 34 725 більше за число 28 816;

2) число 16 546 менше від числа 56 289?

Розв'язання

1) _ 34725       28816        5909

2) _ 56289       16546       39743

Вправа 218 У записі 10 000 000 – 1 265 948 = КИЛСОНЕ буквами позначено цифри числа, що є результатом віднімання. Із цих букв складається прізвище видатного українського композитора. Щоб розшифрувати слово, достатньо в наведеній таблиці під кожною цифрою записати літеру, яка стоїть на місці цієї цифри в правій частині даного запису. Яке прізвище цього композитора?

Розв'язання

1) _ 10000000        1265948        8734052

3742580 ЛИСЕНКО

Вправа 219 У таблиці наведено максимальні відстані від Сонця до деяких планет Сонячної системи:

Меркурій	57 910 000 км
Венера	108 210 000 км
Земля	149 600 000 км
Юпітер	816 355 600 км
Сатурн	1 506 750 000 км
Уран	3 007 665 000 км

Знайдіть, на скільки:

1) Земля знаходиться ближче до Сонця, ніж Сатурн;

_1506750000

   149600000

  1357150000 (км) ‒ на стільки Земля знаходиться ближче до Сонця, ніж Сатурн.

2) Уран розташований далі від Сонця, ніж Меркурій.

_3007665000

    57910000

 2949755000 (км) ‒ на стільки Уран розташований далі від Сонця, ніж Меркурій.

 

Вправа 220 У таблиці наведені розміри штрафів, установлених у Тридесятому царстві за перевищення дозволеної швидкості вуху.

Перевищення Швидкості км/год	10 – 20	21 – 30	31 - 40	Більше 40
Розмір штрафу грн	400	600	800	2000

Який штраф має сплатити автомобіль, якщо він їхав:

1) зі швидкістю 74 км/год на ділянці дороги з максимально дозволеною швидкістю 60 км/год?

74 – 60 = 14 (км/год) – перевищення швидкості.

400 грн – штраф має сплатити водій автомобіля в Тридесятому царстві, якщо він їхав зі швидкістю 74 км/год на ділянці дороги з максимально дозволеною швидкістю 60 км/год.

2) зі швидкістю 128 км/год на ділянці дороги з максимально дозволеною швидкістю 80 км/год?

128 – 80 = 48 (км/год) – перевищення швидкості.

2000 грн – штраф має сплатити водій автомобіля в Тридесятому царстві, якщо він їхав зі швидкістю 128 км/год на ділянці дороги з максимально дозволеною швидкістю 80 км/год.

 

Вправа 221 Власна швидкість катера дорівнює 26 км/год, а його швидкість проти течії — 24 км/год. Знайдіть швидкість катера за течією річки.

Розв'язання

1) 26 ‒ 24 = 2 (км/год) ‒ власна швидкість катера.

2) 26 + 2 = 28 (км/год) ‒ швидкість катера за течією річки.

Відповідь: 28 км/год.

 

Вправа  222 Швидкість катера за течією річки дорівнює 28 км/год, а швидкість течії — 3 км/год. Знайдіть швидкість катера проти течії річки.

 

Вправа  223 Обсяг одного файлу — 306 Мб (мегабайтів), що на 28 Мб більше, ніж обсяг другого файлу. Чи можна записати ці два файли на диск, на якому 600 Мб вільного місця?

^{Короткий запис}

^{I — 306 Мб, що на 28 Мб більше, ніж II}

^{II — ?}

^{Вільного місця — 600 Мб}

 

Вправа 224 Довжина сухопутного кордону України дорівнює 5624 км, а довжина морської берегової лінії (без затоки Сиваш) на 2931 км менша від неї. Чому дорівнює загальна довжина сухопутного кордону і берегової лінії України?

Розв'язання

1) _5624      2931      2693 (км) ‒ довжина берегової лінії.

2) +5624      2693      8317 (км) Відповідь: загальна довжина сухопутного кордону і берегової лінії дорівнює 8317 км.

Вправа 225 Павлина зібрала 74 гриби, що на 16 грибів більше, ніж зібрав Петро. Скільки грибів зібрали Павлина та Петро разом?

Розв'язання

1) 74 ‒ 16 = 58 (гр.) ‒ грибів зібрав Петро.

2) 74 + 58 = 132 (гр.) ‒ грибів зібрали Павлина і Петро разом.

Відповідь: 132 гриби.

 

Вправа 226 Площа Франції дорівнює 544 000 км², що на 94 000 км² більше за площу Швеції, яка на 154 000 км² менша від площі України. Скільки квадратних кілометрів становить площа України?

Розв'язання

1) 544 000 ‒ 94 000 = 450 000 (км²) ‒ площа Швеції.

2) 450 000 + 154 000 = 604 000 (км²) ‒ площа України.

Відповідь: площа України становить 604 000 км².

 

Вправа 227 

2) (7829 ‒ 5878) ‒ (20 000 ‒ 18 453) = 404		_7829   5878   1951	_20000   18453    1547	_1951   1547    404
3) (5689 ‒ 3458 + 1723) ‒ (25 002 ‒ 24 848) + 2967 = 6767
_5689  3458  2231	+2231  1723  3954	_25002  24848     154	_3954    154   3800	+3800   2967   6767

Вправа 228 

1) 84 218 ‒ 57 134 + 34 615 = 61699			_84218  57134  27084	+27084   34615   61699
2) (44 516 ‒ 17 398) ‒ (14 259 + 12 262) = 597		_44516  17398  27118	+14259   12262   26521	_27118  26521     597

Вправа 229 Дорогу з Горіхівки в Гайове побудували за три місяці. За перший місяць побудували частину дороги завдовжки 21 км, за другий — на 8 км меншу, ніж за перший. Разом за ці два місяці побудували на 13 км більше, ніж за третій. Яка відстань між Горіхівкою та Гайовим?

^{Короткий запис}

^{I - 21 км}

^{II - ?, на 8 км менше, ніж I}

^{III - ?, на 13 км менше, ніж I i II разом}

^{Разом - ?}

Розв'язання

1) 21 ‒ 8 = 13 (км) ‒ за другий місяць.

2) 21 + 13 = 34 (км) ‒ за перший і другий місяці разом.

3) 34 ‒ 13 = 21 (км) ‒ за третій місяць.

4) 21 + 21 + 13 = 55 (км) 

Відповідь: відстань між Горіхівкою та Гайовим становить 55 км.

 

Вправа 230 Щукін, Карпов і Сомов відправилися на риболовлю. Разом вони зловили 192 рибки, причому Щукін зловив 53 рибки, що на 15 більше, ніж зловив Карпов. Скільки рибок зловив Сомов?

Розв'язання

1) 53 ‒ 15 = 38 (р.) ‒ зловив Карпов.

2) 53 + 38 = 91 (р.) ‒ зловили Щукін та Карпов разом.

3) 192 ‒ 91 = 101 (р.) ‒ зловив Сомов.

Відповідь: Сомов зловив 101 рибку.

 

Вправа 231 Аладдін, Жасмин і Джин збирали в саду султана персики. Аладдін і Жасмин зібрали разом 112 кг персиків, а Жасмин і Джин — 193 кг персиків. Скільки кілограмів персиків зібрав кожен з них, якщо всього було зібрано 240 кг?

Розв'язання

1) 240 ‒ 112 = 128 (кг) ‒ зібрав Джин.

2) 193 ‒ 128 = 65 (кг) ‒ зібрала Жасмин.

3) 112 ‒ 65 = 47 (кг) ‒ зібрав Алладін.

Відповідь: Алладін зібрав 47 кг персиків, Жасмин ‒ 65 кг, Джин ‒ 128 кг.

 

Вправа 232 У саду Марічка вирощує квіти. Жоржин і троянд у неї 78, а решта — гладіолуси, причому гладіолусів на 9 менше, ніж троянд. Скільки квітів кожного виду росте в саду, якщо всього їх 124?

Розв'язання

1) 124 ‒ 78 = 46 (кв.) ‒ гладіолусів.

2) 46 + 9 = 55 (кв.) ‒ троянд.

3) 78 ‒ 55 = 23 (кв.) ‒ жоржин.

Відповідь: у саду росте 46 гладіолусів, 55 троянд, 23 жоржини.   

 

Завдання 233

Довжина печери Оптимістична, є найбільшою у світі. Довжина ходів печери Озерна (або печери Блакитних озер) дорівнює 128 км, що на 105 км більше за довжину ходів печери Кришталева. Довжина ходів печери Вертеба на 14 км менша від довжини ходів печери Кришталева. Довжина ходів печери Оптимістична на 222 км більша за довжину ходів печери Вертеба. Знайдіть довжину ходів печери Оптимістична.

Розв’язання

1) 128 – 105 = 23 (км) – довжина печери Кришталева.

2) 23 – 14 = 9 (км) – довжина печери Вертеба.

3) 9 + 222 = 231 (км) – довжина печери Оптимістична.

Відповідь: 231 кілометрів.

 

Вправа 234 Перевірте, чи є правильною нерівність:

1) 24 017 ‒ 15 035 < 12 386 ‒ 2987
Правильна 8982 < 9399			_24017  15035   8982	_12386    2987    9399
2) 1674 ‒ (673 + 437) > 1885 ‒ (648 + 664)
Неправильна 564 > 573	+673   437 1110	_1674   1110    564	+648   664   1312	_1885   1312    573

Вправа 235 Перевірте, чи є правильною нерівність:         

6011 ‒ (1539 ‒ 438) < 5791 ‒ (2418 ‒ 1336)
Неправильна 4910 < 4709	_1539    438   1101	_6011  1101  4910	_2418  1336  1082	_5791  1082  4709

Вправа 236 Дії з іменованими величинами

_76 м 39 см   41 м 24 см   35 м 15 см	_64 м 45 см   27 м 86 см   36 м 59 см	_22 км 527 м   17 км 783 м    4 км 744 м
_12 год 24 хв    9 год 18 хв    3 год 06 хв	35 хв 17 с _34 хв 77 с   15 хв 35 с   19 хв 42 с	53 год 32 хв _52 год 92 хв  44 год 56 хв   8 год 36 хв

Вправа 237 

1) _3 дм 2 см      2 дм 6 см             6 см	2) _ 4 км 008 м       1 км 019 м       2 км 989 м
3)  16 год 26 хв    _15 год 86 хв       9 год 52 хв       6 год 34 хв	4)   10 хв 04 с    _  9 хв 64 с        5 хв 40 с        4 хв 24 с

Вправа 238 

Поїзд відходить від станції А о 7 год 37 хв і в той самий день прибуває на станцію В о 9 год 12 хв. Скільки часу рухається поїзд від станції А до станції В?

Розв'язання

9 год 12 хв   _8 год 72 хв    7 год 37 хв    1 год 35 хв Відповідь: поїзд рухається 1 год 35 хв.

Вправа 239 Поїзд відходить від станції А і в той самий день прибуває на станцію В о 15 год 20 хв. О котрій годині поїзд відходить від станції А, якщо на шлях від А до В він витрачає 6 год 48 хв?

Розв'язання

15 год 20 хв _14 год 80 хв    6 год 48 хв    8 год 32 хв  Відповідь: поїзд відходить від станції о 8 год 32 хв.

Вправа 240 Замість зірочок поставте такі цифри, щоб віднімання було виконано правильно.

_ ****      ***        1

_1000    999       1

_*65**    *172    77*69

_86541    9172    77369

_72**    *359   2*19

_7278    4359   2919

Вправа 241 Замість зірочок поставте такі цифри, щоб віднімання було виконано правильно:

_ *567*      *9*7   86*46

_ 95673      8927   86746

_**5*2    7*1*   76746

_84562    7816   76746

_*94*76   1*78*9   13*80*

_294676  157869  136807

Вправа 242** На зупинці з тролейбуса вийшло 15 пасажирів, а ввійшло 8. На другій зупинці вийшло 6 пасажирів і ввійшло 12. Скільки пасажирів було в тролейбусі до першої зупинки, якщо після другої зупинки їх стало 31?

Розв'язання.

1) 15 + 6 = 21 (п.) ‒ пасажирів вийшло.

2) 8 + 12 = 20 (п.) - пасажирів зайшло.

3) 31 + 21 - 20 = 32 (п.) ‒ пасажирів було до першої зупинки. 

Відповідь: до першої зупинки було 32 пасажири.

 

Вправа 243 Між сніданком і обідом Євген з’їв 7 слив з тих, що лежали на тарілці. Після обіду мати поклала туди ще 14 слив. Між обідом і вечерею Євген з’їв 9 слив. Після вечері мати поклала ще 5 слив, і на тарілці стало 20 слив. Скільки слив було на тарілці спочатку?

Розв'язання

1) 7 + 9 = 16 (сл.) ‒ слив з'їв Євген.

2) 14 + 5 = 19 (сл.) ‒ слив поклала мама.

3) 20 + 16 ‒ 19 = 17 (сл.) ‒ слив було спочатку.

Відповідь: на тарілці спочатку було 17 слив.

 

Вправа 244 Першого дня фермер зібрав у своєму саду 26 ящиків яблук, а другого — 14 таких ящиків яблук. Скільки кілограмів яблук зібрав фермер першого дня і скільки — другого, якщо другого дня він зібрав на 192 кг менше, ніж першого?

1) 26 ‒ 14 = 12 (ящ.) ‒ на стільки менше зібрав другого дня, ніж першого. 2) 192 : 12 = 16 (кг) ‒ у одному ящику. 3) 16 • 26 = 416 (кг) ‒ зібрав першого дня. 4) 16 • 14 = 224 (кг) ‒ зібрав другого дня.

_192| 12  12    16   72   72    0

х 16    26    96   32    416

х 16   14   64  16   224

Відповідь: першого дня фермер зібрав 416 кг яблук, другого дня ‒ 224 кг яблук.

 

Вправа 245 Один поїзд був у дорозі 7 год, а другий — 13 год. Другий поїзд пройшов на 360 км більше, ніж перший. Скільки кілометрів пройшов кожний поїзд, якщо вони рухалися з однаковими швидкостями?

1) 13 ‒ 7 = 6 (год) ‒ на стільки більше був у дорозі другий поїзд, ніж перший.

2) 360 : 6 = 60 (км/год) ‒ швидкість поїзда.

3) 60 • 7 = 420 (км) ‒ пройшов один поїзд.

4) 60 • 13 = 60 • (10 + 3) = 780 (км) ‒ пройшов другий поїзд.

Відповідь: перший поїзд пройшов 420 км, другий ‒ 780 км.

 

Вправа 246 Знайдіть значення виразу, обираючи зручний порядок обчислення:

1) (412 + 116) ‒ 112 = (412 ‒ 112) + 116 = 416 

2) (593 + 675) ‒ 275 = (675 ‒ 275) + 593 = 993 

3) 844 ‒ (244 + 318) = 844 ‒ 244 ‒ 318 = 282

4) 729 ‒ (396 + 229) = 729 ‒ 229 ‒ 396 = 104

 

Вправа 247 Знайдіть значення виразу, обираючи зручний порядок обчислення:

1) (176 + 343) ‒ 243 = 176 + (343 ‒ 243) = 276 

2) (684 + 915) ‒ 484 = (684 ‒ 484) + 915 = 1115 

3) 1287 ‒ (487 + 164) = 1287 ‒ 487 ‒ 164 = 636

4) 971 ‒ (235 + 371) = 971 ‒ 371 ‒ 235 = 365

 

Вправа 248 Спростіть вираз:

1) (35 + х ) ‒ 15 = х + 35 ‒ 15 = х + 20 

2) (432 + b) ‒ 265 =  432 ‒ 265 + b = 167 + b

3) 96 ‒ ( m + 48) = 96 ‒ m ‒ 48 = (96 ‒ 48) ‒ m = 48 ‒ m

4) 516 ‒ (216 + х) = 516 ‒ 216 ‒ х = 300 ‒ х 

 

Вправа 249 Спростіть вираз

1) (а + 546) ‒ 328 = а + 546 ‒ 328 = а + 218 

2) (с + 961) ‒ 592 = с + 961 ‒ 592 = с + 369 

3) 272 ‒ (125 + у) = 272 ‒ 125 ‒ y = 147 ‒ y

4) 925 ‒ (р + 735) = 925 ‒ р ‒ 735 = (925 ‒ 735) ‒ р = 190 ‒ р

 

Вправа 250 Як зміниться різниця, якщо:

1) зменшуване збільшити на 8; збільшиться на 8

3) від’ємник збільшити на 5; зменшиться на 5

Висловіть припущення (гіпотезу), як зміниться різниця, якщо:

зменшуване збільшити на число x? Збільшиться на х

a ‒ b, (a + x) ‒ b = (a ‒ b) + х

від’ємник збільшити на число x? Зменшиться на х

a ‒ b, a ‒ (b + x) = (a ‒ b) ‒ х

 

Вправа 251 У двоцифровому числі 6 десятків. Між цифрами цього числа вписали цифру 0. На скільки отримане трицифрове число більше за дане двоцифрове?

Розв'язання

_60*    6*  540

Відповідь: отримане трицифрове число більше на 540, ніж двоцифрове.

 

Вправа 252 У записі 1 2 3 4 5 6 7 8 9 поставте між деякими цифрами знак ≪+≫ або знак ≪‒≫ так, щоб значення отриманого виразу дорівнювало 100.

Розв'язання

123 + 45 ‒ 67 + 8 ‒ 9 = 100

 

Вправи для повторення.

Вправа 253

1) 25 • (63 ‒ 741 : 19) = 600	_741 | 19  57     39  171  171     0	_ 63    39    24	х 25   24  100  50    600
2) (900 ‒ 7218 : 9) • 12 = 1176	_7218 | 9      72       802      18       18        0	_ 900    802      98	х  98     12   196   98     1176
3) 3926 : 13 • 8 + 2584 = 5000	_3926 | 13      39       302     26      26       0	+ 2584    2416    5000	х 302      8   2416
4) 690 ‒ 2944 : 64 • 15 = 690 ‒ 690 = 0		_2944 | 64  256     46   384   384      0	х 46    15  230  46    690

Вправа 254 На відрізку АВ позначили точку С. Відстань між серединами відрізків АС і ВС становить 12 см. Яка довжина відрізка АВ?

Розв'язання

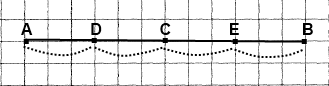
АВ = АС + СВ = (АD + DС) + (СЕ + ЕВ) = (АD + ЕВ) + (DС + СЕ) =

= 2(DС + СЕ) = 2 • 12 см = 24 см ‒ довжина відрізка АВ.

 

Вправа 255 Накресліть координатний промінь і позначте на ньому точки А (1), В (7), С (3), D (9). На цьому ж промені позначте точки, які віддалені від точки В: 1) на 3 одиничних відрізки; 2) на 8 одиничних відрізків. Знайдіть координати цих точок.

Розв'язання

1) 7 + 3 = 10, Е(10)     7 - 3 = 4, E'(4)

2) 7 + 8 = 15, F(15)

Учимося застосовувати математику

Вправа 256 У магазині купили 2 кг 400 г картоплі, 1 кг 140 г моркви, 1 кг 70 г цибулі та 700 г солоних огірків. Чи донесе покупець придбані овочі з магазину додому в пакеті, на якому є маркування, зображене на рисунку 75?

Розв'язання

2 кг 400 г + 1 кг 140 г + 1 кг 70 г + 700 г = 4 кг 1310 г = 5 кг 310 г

5 кг 310 г > 5 кг

Відпвідь: не донесе. 

 

Вправа 257 Із села Південне до села Сонячне ведуть три маршрути (рис. 76). У баку автомобіля є 30 л бензину, витрата якого на проїзд 100 км становить 10 л. Який маршрут має обрати водій цього автомобіля, щоб доїхати з Південного в Сонячне, не заправляючись.

^{Короткий запис}

^{10 л — 100 км}

^{30 л — ?}

^{Чи вистачить — ?}

Розв'язання.

1) 30 : 10 = 3 (р.) ‒ у стільки разів більше бензину.

2) 100 • 30 = 300 (п.) ‒ на таку відстань вистачить бензину.

 

Вправа 258  Дані про виступи україн­ських школярів на Міжнародних математич­них олімпіадах протягом 2015-2021 років.

Місце проведення	Рік	Кількість медалей
		Золоті	Срібні	Бронзові	Разом медалей
Таїланд	2015	2	3	1	6
Гонконг	2016	0	2	4	6
Бразилія	2017	1	2	2	5
Румунія	2018	4	2	0	6
Велика Британія	2019	1	4	1	6
Росія (онлайн)	2020	-	6	0	6
Росія (онлайн)	2021	3	2	1	6
Усього медалей		11	21	9	41

Вправа 259 (Знайдіть помилку) Василь Ледащенко замість того, щоб самостійно розв’язати задачу 249 (3), скористався ГДЗ1. Знайдіть помилку в цьому «розв’язанні». 272 – (125 + y) = 272 – 125 – y = 147 – y.

 

Задача від Мудрої Сови

Вправа 260 У скільки разів шлях по сходах з першого поверху на десятий довший за шлях з першого поверху на другий? З першого на другий поверх треба пройти 1 поверх, а з першого на десятий ‒ дев'ять поверхів, тому шлях у 9 разів довший.

 

--------------------------- у підручнику за 2013, 2018 роки ---------------------------- 

Вправа 216 Відстань між Сімферополем і Запоріжжям, що становить 365 км, Омеля подолав на своїй печі за три дні. За перших два дні він проїхав 246 км, а за перший і третій — 268 км. Скільки кілометрів проїжджала піч кожного дня?

Розв'язання.

1) 365 ‒ 246 = 119 (км) ‒ подолав третього дня.

2) 268 ‒ 119 = 149 (км) ‒ подолав першого дня.

3) 246 ‒ 149 = 97 (км) ‒ подолав другого дня.

Відповідь: першого дня піч проїхала 149 км, другого ‒ 97 км, третього ‒ 119 км.

 

Вправа 218* Юрко збирає моделі автомобілів, літаків і пароплавів, причому автомобілів і літаків у нього 56 моделей, а літаків — на 12 моделей більше, ніж пароплавів. Скільки моделей кожного виду є в Юрка, якщо вся його колекція складається з 82 моделей?

Розв'язання

1) 82 ‒ 56 = 26 (м.) ‒ пароплавів.

2) 26 + 12 = 38 (м.) ‒ літаків.

3) 56 ‒ 38 = 18 (м.) ‒ автомобілів.

Відповідь: у Юрка є 26 моделей пароплавів, 38 моделей літаків, 18 моделей автомобілів.

 

Вправа 236** Заповніть наявні пропуски в таблиці, у якій наведено дані про виступи українських школярів на Міжнародних математичних олімпіадах протягом 2003‒2012 років.

Місце проведення	РІК	Золоті медалі	Срібні медалі	Бронзові медалі	Разом медалей
Японія	2003	1	2	3	6
Греція	2004	1	5	0	6
Мексика	2005	2	2	2	6
Словенія	2006	1	2	2	5
В'єтнам	2007	3	1	2	6
Іспанія	2008	2	2	2	6
Німеччина	2009	3	1	2	6
Казахстан	2010	1	2	3	6
Нідерланди	2011	1	2	3	6
Аргентина	2013	0	3	2	5
Всього	медалей	15	22	21	58

Вправа 207 У серпні корова Зірочка дала 278 л молока, а у вересні — на 26 л менше. Скільки літрів молока дала Зірочка за ці два місяці?

Розв'язання

1) 278 ‒ 26 = 252 (л) ‒  у вересні.

2) 278 + 252 = 530 (л) ‒ за два місяці.

Відповідь: корова Зірочка за два місяці дала 530 літрів молока.

 

Вправа 212* Петро, Василь і Микола здали на завод цукрові буряки. Петро здав 56 ц буряків, що на 18 ц більше, ніж Василь. Разом вони здали на 28 ц буряків більше, ніж Микола. Скільки всього центнерів цукрових буряків вони здали?

Розв'язання

1) 56 ‒ 18 = 38 (ц) ‒ здав Василь.

2) 56 + 38 = 94 (ц) ‒ здали Петро та Василь разом.

3) 94 ‒ 28 = 66 (ц) ‒ здав Микола.

4) 56 + 38 + 66 = 160 (ц)

Відповідь: хлопці здали 160 ц цукрових буряків.

 

Вправа 213 За три дні Рокфор з’їв 230 головок сиру. За перший день він з’їв 74 головки, що на 16 головок більше, ніж за другий. Скільки сиру з’їв Рокфор за третій день?

Розв'язання

1) 74 ‒ 16 = 58 (г.) ‒ за другий день.

2) 74 + 58 = 132 (г.) ‒ за перший та другий день разом.

3) 230 ‒ 132 = 98 (г.) ‒ за третій день.

Відповідь: за третій день Рокфор з’їв 98 головок сиру.

 

Вправа 237**  Дані про виступи україн­ських школярів на Міжнародних математич­них олімпіадах протягом 2008-2017 років.

Місце проведення	Рік	Кількість медалей
		Золоті	Срібні	Бронзові	Разом медалей
Іспанія	2008	2	2	2	6
Німеччина	2009	3	1	2	6
Казахстан	2010	1	2	3	6
Нідерланди	2011	1	2	3	6
Аргентина	2012	0	3	2	5
Колумбія	2013	1	3	1	5
ЮАР	2014	2	3	1	6
Таїланд	2015	2	3	1	6
Гонконг	2016	0	2	4	6
Бразилія	2017	1	2	2	5
Усього медалей		13	23	21	57

 Інші завдання дивись тут ...