© ГДЗ 8next.com, 2013, 2018, 2022
Розв’язуємо усно
Завдання 1 Яких чисел не вистачає в ланцюжку обчислень?
Розв'язання

Завдання 2 Розв'яжіть рівняння:
|
1) х + 13 = 28 х = 28 ‒ 13 х = 15 |
2) 20 ‒ х = 12 х = 20 ‒ 12 х = 8 |
3) х ‒ 11 = 79 х = 79 + 11 х = 90 |
4) 10 + х = 16 х = 16 ‒ 10 х = 6 |
|
1) 2х ‒ 3 = 7 2) х + 20 = 20 + х 3) 36 ‒ Зх = 20 |
4) х • х • х + 25 = 150 5) 0 • х = 10 6) х + 12 = 22 ‒ х |
Розв'язання
1) 2 • 5 ‒ 3 = 7; 7 = 7
2) 5 + 20 = 20 + 5; 25 = 25
3) 36 ‒ З • 5 = 36 ‒ 15 = 21; 21 ≠ 20
4) 5 • 5 • 5 + 25 = 125 + 25 = 150; 150 = 150
5) 0 • 5 = 0; 0 ≠ 10
6) 5 + 12 = 22 ‒ 5; 17 = 17
Відповідь: число 5 є коренем рівнянь 1), 2), 4), 6).
Завдання 4 У Петрика і Михайлика було порівну цукерок. Петрик віддав Михайликові 8 цукерок. На скільки цукерок у Михайлика стало більше, ніж у Петрика?
Розв'язання
Нехай х (ц.) ‒ було цукерок у кожного хлопця, тоді
(х ‒ 8) (ц) ‒ цукерок стало у Петрика,
(х + 8) (ц) ‒ цукерок стало в Михайлика.
х + 8 ‒ (х ‒ 8) = х + 8 ‒ х + 8 = 16 (ц.) ‒ на стільки цукерок у Михайлика стало більше, ніж у Петрика.
Відповідь: у Михайлика стало на 16 цукерок більше, ніж у Петрика.
Завдання 5 (Задача-жарт) Двоє коней пробігли 20 км. Скільки кілометрів пробіг кожний кінь? Кожний кінь пробіг 20 км.
Вправи
Вправа 304 Як можна позначити кут, зображений на рисунку 82? Укажіть його вершину та сторони.
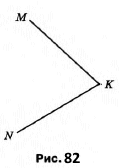
Позначення кута: ∠MKN, ∠NKM, ∠K. Вершина: K. Сторони: MK, NK.
Вправа 305 На якому з рисунків 83, а, б, в промінь ОК є бісектрисою кута АОВ.
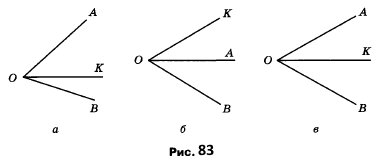
На рисунку в) промінь ОК ділить кут О навпіл, тому є бісектрисою кута.
Вправа 306 Назвіть усі кути, зображені на рисунку 84.
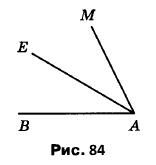
∠ВАМ, ∠ВАЕ, ∠ЕАМ
Вправа 307 Накресліть кут AOC і проведіть промінь OM між його сторонами. Запишіть кути, які утворилися..
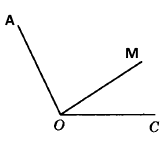
∠АОМ, ∠МОС, ∠АОС
Вправа 308 Які з променів, зображених на рисунку 85, перетинають сторону кута ВОС?
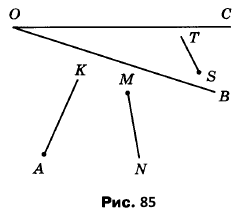
Промінь АК (перетинає дві сторони), промінь ST (перетинає одну сторону).
Вправа 309 Які з променів, зображених на рисунку 86, перетинають сторону кута ВОС?
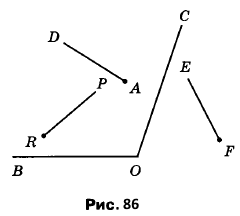
Промені RP, FE
Вправа 310 Накресліть кут MNE і проведіть промені NA і NC між його сторонами. Запишіть усі кути, що утворилися.
Розв'язання.
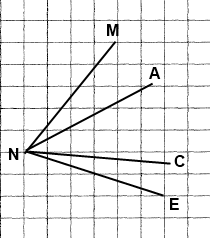
Кути: ∠MNE, ∠MNA, ∠ANC, ∠CNE, ∠MNC, ∠ANE
Вправа 311 На рисунку 87 <ABE = <CBF. Чи є ще на цьому рисунку рівні кути?
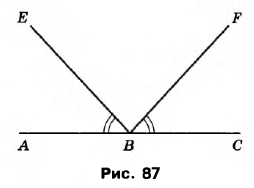
∠ABF = ∠ЕBС
Вправа 312 На рисунку 88 <AOB = <DOE, <BOC = <COD. Чи є ще на цьому рисунку рівні кути?
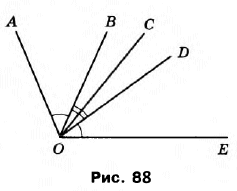
∠AOС = ∠ЕOС, ∠АОD = ∠ЕОВ
Вправа 313 На рисунку 89 кути FOK і МОЕ рівні. Які ще кути, зображені на цьому рисунку, рівні?
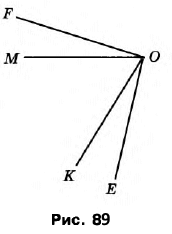
∠FOМ = ∠КОЕ
Вправи для повторення
Вправа 314 Складіть числовий вираз і знайдіть його значення:
1) добуток суми чисел 18 і 20 та числа 8;
1) (18 + 20) • 8 = (10 + 8 + 20) • 8 = 80 + 64 + 160 = 304
2) частка різниці чисел 128 і 29 та числа 11;
(128 ‒ 29) : 11 = 99 : 11 = 9
3) частка добутку чисел 15 і 6 та їх різниці.
(15 • 6) : (15 ‒ 6) = 90 : 9 = 10
Вправа 315 Учні п’ятих класів їхали двома автобусами на екскурсію. Коли з одного автобуса, у якому було 42 учні, 8 учнів перейшли у другий автобус, то в обох автобусах учнів стало порівну. Скільки учнів було в другому автобусі спочатку?
Розв'язання
1) 42 ‒ 8 = 34 (уч.) ‒ учнів стало в першому автобусі.
2) 34 ‒ 8 = 26 (уч.) ‒ учнів у другому автобусі спочатку.
Відповідь: у другому автобусі спочатку було 26 учнів.
Задача від Мудрої Сови
Вправа 316 Відстань між містами А і В дорівнює З0 км. Із міста А в місто В виїхав велосипедист, який рухався зі швидкістю 15 км/год. Одночасно з ним з міста В у напрямку міста А вилетів птах зі швидкістю З0 км/год. Зустрівшись із велосипедистом, птах розвернувся і полетів назад. Прилетівши в місто В, він знову розвернувся і полетів назустріч велосипедисту. Зустрівшись із ним, птах розвернувся і полетів назад у місто В. Птах літав у такий спосіб доти, доки велосипедист не приїхав у місто В. Скільки кілометрів пролетів птах?
Розв'язання
1 спосіб
1) 30 км : 15 км/год = 2 год ‒ час руху велосипедиста.
Примітка. 2 год - це час руху і птаха, бо птах літав доти, доки велосипедист не приїхав у місто.
2) 30 км/год • 2 год = 60 км ‒ відстань пролетів птах за 2 год.
2 спосіб
1) 30 км/год : 15 км/год = 2 (рази) - у стільки разів більша швидкість птаха, ніж велосипедиста.
2) 30 км • 2 = 60 км ‒ відстань пролетів птах.
Відповідь: птах пролетів 60 км.
------------------------ до підручника 2013, 2018 років ----------------
Вправа 315 Розв'яжіть рівняння:
|
1) х + 504 968 = 1 017 216 х = 1 017 216 ‒ 504 968 х = 512 248 |
_1017216 504968 512248 |
|
2) 120 340 526 ‒ х = 7 908 049 х = 120 340 526 ‒ 7 908 049 х = 112 432 477 |
_120340526 7908049 112432477 |
Вправа 296 На XXX Олімпійських іграх, що відбулися у 2012 р. в Лондоні (Велика Британія), олімпійська збірна України здобула 20 медалей. Наші спортсмени отримали 11 золотих і срібних медалей, а золотих і бронзових — 15. Скільки медалей кожного виду завоювала на цій олімпіаді наша збірна?
Розв'язання.
1) 20 ‒ 11 = 9 (м.) ‒ бронзових медалей.
2) 15 ‒ 9 = 6 (м.) ‒ золотих медалей.
3) 11 ‒ 6 = 5 (м.) ‒ срібних медалей.
Відповідь: збірна завоювала 6 золотих медалей, 5 срібних медалей і 9 бронзових медалей.