© ГДЗ 8next.com, 2013, 2018, 2022
Запитання
1. Який чотирикутник називають прямокутником?
Якщо в чотирикутнику всі кути прямі, то його називають прямокутником.
2. Що називають довжиною і шириною прямокутника?
Сусідні сторони прямокутника називають його довжиною і шириною.
3. Яку властивість мають протилежні сторони прямокутника?
Протилежні сторони (сторони, що не мають спільних вершин) прямокутника рівні.
4. Яку фігуру називають квадратом?
Прямокутник, у якого всі сторони рівні, називають квадратом.
5. За якою формулою обчислюють периметр прямокутника?
Р = 2а + 2Ь = 2 (а + b), де а і Ь — сторони прямокутника.
6. За якою формулою обчислюють периметр квадрата?
Р = 4а, де а — сторона квадрата.
Розв’язуємо усно
Завдання 1 Один із доданків збільшили на 19. Як треба змінити другий доданок, щоб сума не змінилася? Сума збільшиться на 19. Щоб сума не змінилась її треба зменшити на 19, тому другий доданок треба зменшити на 19.
Завдання 2 Від’ємник зменшили на 47. Як треба змінити зменшуване, щоб різниця не змінилася? Різниця збільшилась на 47. Щоб різниця не змінилась її треба зменшити на 47, тому зменшуване треба зменшити на 47.
Завдання 3 Зменшуване збільшили на 26. Як треба змінити від’ємник, щоб різниця не змінилася? Різниця збільшилась на 26. Щоб різниця не змінилась, її треба зменшити на 26, тому треба від'ємник збільшити на 26.
Завдання 4 Периметр рівнобедреного трикутника дорівнює 32 см, а одна з його сторін — 12 см. Знайдіть довжини двох інших сторін трикутника. Скільки розв’язків має задача?
Розв'язання
1 варіант
1) 32 ‒ 12 = 20 (см) ‒ сума довжин бічних сторін.
2) 20 : 2 = 10 (см) ‒ довжина бічної сторони рівнобедреного трикутника.
Відповідь: бічні сторони рівнобедреного трикутника дорівнюють по 10 см.
2 варіант
1) 12 • 2 = 24 (см) ‒ сума довжин бічних сторін.
2) 32 ‒ 24 = 8 (см) ‒ довжина основи рівнобедреного трикутника.
Відповідь: бічна сторона рівнобедреного трикутника дорівнює 12 см, основа ‒ 8 см.
Завдання 5 Знайдіть сторону рівностороннього трикутника, якщо вона менша від його периметра на 10 см.
Розв'язання
Нехай х (см) ‒ сторона рівностороннього трикутника, тоді 3х (см) ‒ периметр рівностороннього трикутника.
3х ‒ х = 10
2х = 10
х = 10 : 2
х = 5 (см)
Відповідь: сторона рівностороннього трикутника дорівнює 5 см.
Завдання 6 Обчисліть значення у за формулою у = х • х + 12, якщо:
1) х = 1;
Якщо х = 1, тоді у = х • х + 12 = 1 • 1 + 12 = 13
2) х = 10.
Якщо х = 10, тоді у = х • х + 12 = 10 • 10 + 12 = 112
Вправи
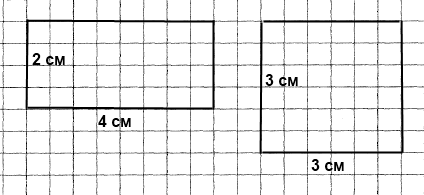
Вправа 387° Побудуйте: 1) прямокутник, сторони якого дорівнюють 4 см і 2 см; 2) квадрат зі стороною 3 см.
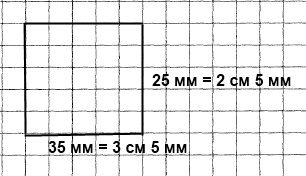
Вправа 388° Побудуйте прямокутник, сторони якого дорівнюють 25 мм і 35 мм.
Вправа 389° Обчисліть периметр:
1) прямокутника, сторони якого дорівнюють 42 см і 23 см;
Р = (42 см + 23 см) • 2 = 130 см = 1 м 30 см
Відповідь: периметр прямокутника 1 м 30 см.
2) квадрата із стороною 8 дм.
Р = 8 дм • 4 = 32 дм
Відповідь: периметр квадрата 32 дм.
Вправа 390°Знайдіть периметр прямокутника, сторони якого дорівнюють 13 мм і 17 мм.
Розв'язання
Р = (13 мм + 17 мм) • 2 = 60 мм = 6 см
Відповідь: периметр прямокутника 6 см.
Вправа 391° Довжина однієї із сторін прямокутника дорівнює 14 см, що на 5 см більше за довжину другої сторони. Знайдіть периметр прямокутника.
Розв'язання
1) 14 ‒ 5 = 9 (см) ‒ довжина другої сторони.
2) (14 + 9) • 2 = 46 (см) ‒ периметр прямокутника.
Відповідь: периметр прямокутника 46 см.
Вправа 392 Периметр прямокутника дорівнює 34 см, а одна із його сторін — 12 см. Знайдіть довжину сусідньої сторони прямокутника.
Розв'язання
1) 12 • 2 = 24 (см) ‒ сума двох протилежних сторін прямокутника.
2) 34 ‒ 24 = 10 (см) ‒ сума інших протилежних сторін прямокутника.
3) 10 см : 2 = 5 (см) ‒ довжина сусідньої сторони прямокутника.
Відповідь: довжина сусідньої сторони прямокутника дорівнює 5 см.
Вправа 393 Одна сторона прямокутника дорівнює 8 см, а сусідня — у 4 рази більша. Знайдіть периметр прямокутника.
Короткий запис
I — 8 cv
II — ?, у 4 рази більша
Периметр — ?
Розв'язання
1) 8 • 4 = 32 (см) ‒ довжина сусідньої сторони.
2) (8 + 32) • 2 = 80 (см) ‒ периметр прямокутника.
Відповідь: периметр прямокутника 80 см.
Вправа 394 Квадрат зі стороною 12 см і прямокутник, одна із сторін якого дорівнює 8 см, мають рівні периметри. Знайдіть невідому сторону прямокутника.
Розв'язання
1) 12 • 4 = 48 (см) ‒ периметр квадрата/ прямокутника.
2) 8 • 2 = 16 (см) ‒ сума двох протилежних сторін прямокутника.
3) 48 ‒ 16 = 32 (см) ‒ сума двох інших протилежних сторін прямокутника.
4) 32 : 2 = 16 (см) ‒ довжина невідомої сторони прямокутника.
Відповідь: довжина невідомої сторони 16 см.
Вправа 395 Два рівних прямокутники приклали один до одного так, що їхні більші сторони збіглися. У результаті цього утворився квадрат, периметр якого дорівнює 432 см. Знайдіть периметр прямокутника.
Розв'язання
1) 432 : 4 = 108 (см) ‒ довжина більшої сторони прямокутника.
2) 108 : 2 = 54 (см) ‒ довжина меншої сторони прямокутника.
3) (108 + 54) • 2 = 162 • 2 = 324 (см) ‒ периметр прямокутника.
Відповідь: периметр прямокутника дорівнює 324 см.
Вправа 396 Прямокутник, сусідні сторони якого дорівнюють 42 см і 14 см, та квадрат мають рівні периметри. Знайдіть сторону квадрата.
Розв'язання
1) (42 + 14) • 2 = 112 (см) ‒ периметр прямокутника.
2) 112 : 4 = 28 (см) ‒ довжина сторони квадрата.
Відповідь: довжина сторони квадрата 28 см.
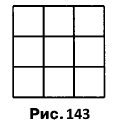
Вправа 397** Скільки квадратів зображено на рисунку 143? 14 квадратів
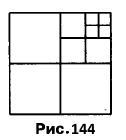
Вправа 398 Скільки квадратів зображено на рисунку 144? 13 квадратів
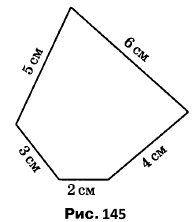
Вправа 399 З куска дроту зробили модель п’ятикутника (рис. 145). Які з моделей перелічених фігур, довжини сторін яких, виражені в сантиметрах, є натуральними числами, можна зробити з цього куска дроту: 1) квадрат; 2) п’ятикутник, усі сторони якого рівні; 3) рівносторонній трикутник?
Розв'язання
Р = 5 см + 6 см + 4 см + 2 см + 3 см = 20 см.
1) можна зробити квадрат зі стороною 5 см (20 см : 4 = 5 см)
2) можна зробити п'ятикутник зі сторонами 4 см кожна (20 см : 5 = 4 см)
3) не можна зробити рівносторонній трикутник, бо число 20 не ділиться націло на 3.
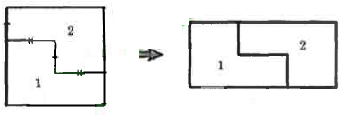
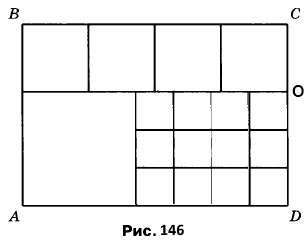
Вправа 400 Прямокутник ABCD розрізали на квадрати так, як показано на рисунку 146. Сторона найменшого квадрата дорівнює 4 см. Знайдіть довжини сторін прямокутника ABCD.
Розв'язання
Сторона найбільшого квадрата 4 см • 3 = 12 см.
АD = BC = 12 см • 2 + 4 см = 28 см
ВА = СD = CO + OD = 28 см : 4 + 4 см • 3 = 7 см + 12 см = 19 см
Вправа 401 Нарисуйте прямокутник, сусідні сторони якого дорівнюють 3 см і 6 см. Розбийте його на три рівні прямокутники. Обчисліть периметр кожного з утворених прямокутників. Скільки розв’язків має задача? Два розв'язки
Розв'язання
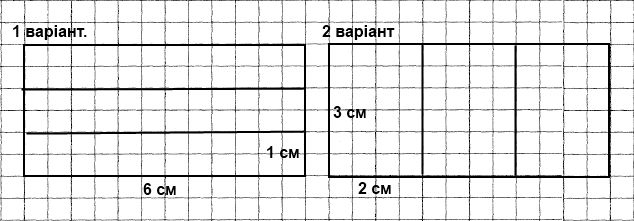
1 варіант
Р = (6 см + 1 см) • 2 = 14 см ‒ периметр малого прямокутника.
2 варіант
Р = (3 см + 2 см) • 2 = 10 см ‒ периметр малого прямокутника.
Вправа 402 Чи є серед прямокутників з периметром 12 см такий, що його можна розбити на два рівних квадрати? У разі позитивної відповіді виконайте рисунок та обчисліть периметр кожного з утворених квадратів.
Розв'язання
12 : 2 = 6 см ‒ сума довжини та сторони прямокутника.
Розглянемо прямокутник зі сторонами 4 см і 2 см
Через середину сторони 4 см проведемо відрізок, щоб розбити прямокутник, тоді матимемо два квадрати зі стороною 2 см.
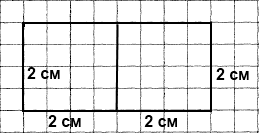
Р = 2 см • 4 = 8 см ‒ периметр квадрата.
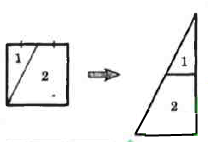
Вправа 403 Як треба розрізати квадрат на чотири рівні частини, щоб із них можна було скласти два квадрати?
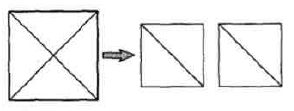
Вправа 404 Як треба розрізати рівнобедрений прямокутний трикутник на чотири рівні частини, щоб із них можна було скласти квадрат?
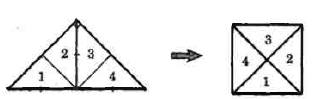
Вправа 405 Як треба розрізати прямокутник із сторонами 8 см і 4 см на чотири частини, щоб із них можна було скласти квадрат?
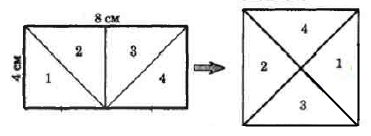
Вправа 406 Як треба розрізати квадрат на трикутник і чотирикутник, щоб із них можна було скласти трикутник?
Вправи для повторення
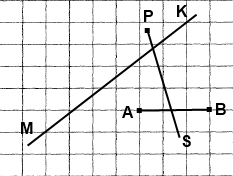
Вправа 407 Проведіть пряму МК, промінь PS і відрізок АВ так, щоб промінь PS перетинав відрізок АВ і пряму МК, а пряма МК не перетинала відрізок АВ.
Вправа 408 У крамниці є лимони, апельсини та мандарини, загальна маса яких дорівнює 740 кг. Якби продали 55 кг лимонів, 36 кг апельсинів и 34 кг мандаринів, то маси лимонів, апельсинів і мандаринів, що залишилися, виявилися б рівними. Скільки кілограмів фруктів кожного виду є в крамниці?
Розв'язання
1) 55 + 36 + 34 = 125 (кг.) ‒ продали фруктів.
2) 740 ‒ 125 = 615 (кг) ‒ усіх фруктів залишилось.
3) 615 : 3 = 205 (кг) ‒ фруктів кожного виду залишилось.
4) 205 + 55 = 260 (кг) ‒ лимонів є в крамниці.
5) 205 + 36 = 241 (кг) ‒ апельсинів є в крамниці.
6) 205 + 34 = 239 (кг) ‒ мандаринів є в крамниці.
Відповідь: у крамниці є 260 кг лимонів, 241 кг апельсинів і 239 кг мандаринів.
Вправа 409
1) Знайдіть суму коренів рівнянь (х ‒ 18) ‒ 73 = 39 і 24 + (у ‒ 52) = 81
Розв'язання
|
(х ‒ 18) ‒ 73 = 39 х ‒ 18 = 39 + 73 х ‒ 18 = 112 х = 112 + 18 х = 130 |
24 + (у ‒ 52) = 81 у ‒ 52 = 81 ‒ 24 у ‒ 52 = 57 у = 57 + 52 у = 109 |
Сума коренів рівняння: х + у = 130 + 109 = 239 |
2) Знайдіть суму коренів рівнянь (65 ‒ х) + 14 = 51 і (у + 16) + 37 = 284
Розв'язання
|
(65 ‒ х) + 14 = 51 65 ‒ х = 51 ‒ 14 65 ‒ х = 37 х = 65 ‒ 37 х = 28 |
(у + 16) + 37 = 284 у + 16 = 284 ‒ 37 у + 16 = 247 у = 247 ‒ 16 у = 231 |
Сума коренів рівняння: х + у = 28 + 231 = 259 |
Вправа 410 (Знайдіть помилку) Василь Ледащенко замість того, щоб самостійно розв’язати задачу 396, скористався ГДЗ і списав таке: 42 + 14 = 56 (см); сторона квадрата дорівнює 56 : 4 = 14 (см). Знайдіть помилку в цьому «розв’язанні».
Правильне розв'язання задачі.
1) (42 + 14) • 2 = 112 (см) ‒ периметр прямокутника.
2) 112 : 4 = 28 (см) ‒ довжина сторони квадрата.
Учимося застосовувати математику
Вправа 411 Парк має форму прямокутника, сусідні сторони якого дорівнюють 460 м і 240 м. Навколо парку встановлено огорожу, а в парку на відстані 2 м від огорожі вздовж неї прокладено бігову доріжку, яка також має форму прямокутника. Яринка, яка дотримується здорового способу життя, щоранку до початку уроків бігає по цій доріжці, двічі оббігаючи парк. Яку відстань пробігає Яринка?
Розв’язання
1) 460 – (2 + 2) = 456 (м) – довжина прямокутної ділянки бігової доріжки.
2) 240 – (2 + 2) = 236 (м) – ширина прямокутної ділянки бігової доріжки.
3) (456 + 236) • 2 = 692 • 2 = 1384 (м) – периметр прямокутної доріжки.
4) 1384 • 2 = 2768 (м) = 2 км 768 м – пробігає Яринка.
Відповідь: Яринка пробігає 2 км 768 м.
Вправа 412 У спортивному залі потрібно розмітити різними кольорами баскетбольний і волейбольний майданчики, які мають форму прямокутників. Сусідні сторони баскетбольного майданчика дорівнюють 26 м і 14 м, а волейбольного — 18 м і 9 м. Щоб провести лінію завдовжки 1 м, потрібно 50 г фарби. Скільки потрібно фарби, щоб обвести лініями контури обох майданчиків?
Розв’язання
1) (26 + 14) • 2 = 80 (м) – периметр баскетбольного майданчика.
2) (18 + 9) • 2 = 54 (м) – периметр волейбольного майданчика.
3) 80 + 54 = 134 (м) – довжина усіх ліній.
4) 50 • 134 = 6700 (г) = 6 кг 700 г – потрібно фарби.
Відповідь: для обох майданчиків потрібно 6 кг 700 г фарби.
Вправа 413
Від міського будинку, у якому проживає сім’я Петренків, до їхньої дачі можна доїхати автобусом, або електричкою, або маршрутним таксі. У таблиці наведено час, який потрібно витратити на кожну ділянку шляху. За який найменший час сім’я Петренків може доїхати до дачі? Яким видом транспорту вони мають
при цьому скористатися?
|
Вид транспорту |
Час на дорогу від будинку до зупинки транспорту |
Час на проїзд у транспорті |
Час на дорогу від зупинки транспорту до дачі |
|
Автобус |
10 хв |
1 год 15 хв |
5 хв |
|
Електричка |
8 хв |
56 хв |
10 хв |
|
Маршрутне таксі |
7 хв |
1 год 5 хв |
8 хв |
Розв’язання
1) 10 хв + 1 год 15 хв + 5 хв = 1 год 30 хв – час автобусом.
2) 8 хв + 56 хв + 10 хв = 74 хв = 1 год 14 хв – час електричкою.
3) 7 хв + 1 год 05 хв + 8 хв = 1 год 20 хв – час маршрутним таксі.
Відповідь: найменший час електричкою 1 год 14 хв.
Задача Мудрої Сови
Вправа 414 Як за допомогою п’ятилітрового бідона й трилітрової банки набрати на березі річки 4 л води?
Розв'язання
3 + (2 + 1) ‒ 5 + 3 = 4 (л)
1. Набрати банкою 3 л води і вилити в бідон.
2. Ще раз набрати банкою 3 л води і наповнити бідон до 5 л, при цьому в банці залишиться 1 л води.
3. Вилити всю воду з бідона і перелити в нього 1 л води, що залишилася в банці.
4. Набрати банкою 3 л води і вилити в бідон, в якому буде 4 л води.
---------------------------- у виданнях 2013, 2018 років ----------------------------------
Завдання 4 Кожна сторона трикутника дорівнює 12 см. Як називають такий трикутник? Чому дорівнює його периметр?
Р = 12 см • 3 = 36 см ‒ периметр трикутника.
Як називають такий трикутник? Рівносторонній трикутник.
Вправа 384* Як треба розрізати квадрат із стороною 6 см на дві частини по ламаній, яка містить три ланки, щоб з отриманих частин можна було скласти прямокутник?