Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

 

Розв'язуємо усно

Завдання 1 Які цифри можна підставити замість зірочки, щоб дріб 372/3*5 був правильним?

Розв’язання

^{Дріб, у якого чисельник менший від знаменника, називають правильним.}

Маємо 372 < 3*5

Відповідь: при 7, 8, 9.

 

Завдання 2 На шаховій дошці стоять 14 фігур, з яких 5 — чорні.

^{14 – 5 = 9 (ф.) – білі фігури.}

Яку частину всіх фігур становлять білі фігури? 9/14

Яку частину чорних фігур становлять білі? 9/5

Яку частину білих фігур становлять чорні? 5/9

 

Завдання 3 Від суми чисел 19 і 23 відніміть 34.

(19 + 23) – 34 = 42 – 34 = 8

 

Завдання 4 До суми чисел 18 і 16 додайте їх різницю.

(18 + 16) + (18 – 16) = 34 + 2 = 36

 

Завдання 5 Подвойте суму 37 + 100 + 63.

(37 + 100 + 63) • 2 = 200 • 2 = 400

 

Завдання 6 Назвіть у порядку спадання числа: 9/49; 8/49; 1 (49/49); 24/49; 50/49; 100/49

100/49, 50/49, 1, 24/49, 9/49, 8/49.

 

Вправи

Вправи 800° Виконайте дії:

1) 7/18 + 5/18 = (7+5)/18 = 12/18

2) 11/24 + 8/24 = (11+8)/24 = 19/24

3) 23/47 – 14/47 = (23–14)/47 = 9/47

4) 31/58 – 16/58 = (31–16)/58 = 15/58

5) 3/29 + 6/29 – 8/29 = (3+6–8)/29 = 1/29

6) 29/64 – 14/64 – 9/64 = (29–14–9)/64 = 6/64

 

Вправи 801° Виконайте дії:

1) 4/15 + х = 11/15     х = 11/15 – 4/15     х = (11–4)/15     х = 7/15

2) 16/21 – х = 9/21     х = 16/21 – 9/21     х = (16–9)/21     х = 7/21

3) х – 4/35 = 12/35     х = 12/35 + 4/35     х = (12+4)/35     х = 16/35

Вправи 803° 

1) 7/10 + х = 9/10     х = 9/10 – 7/10     х = (9–7)/10     х = 2/10

2) 29/32 – х = 15/32    х = 29/32 – 15/32    х = (29–15)/32    х = 14/32

Вправи 804° За перший день Михайлик прочитав 5/16 книжки, а за другий день — 7/16 книжки. Яку частину книжки прочитав Михайлик за два дні?

^{Короткий запис}

^{I — ?, 5/16 книжки}

^{II — ?, 7/16 книжки}

^{Разом — ?}

Розв’язання

5/16 + 7/16 = (5+7)/16 = 12/16 – частину книжки прочитав за два дні.

Відповідь: за два дні Михайлик прочитав 12/16 частину книжки.

 

Вправи 805° Для перевезення вантажу використали кілька вантажівок. На одну з них поклали 6/19 вантажу, а на другу — 8/19 вантажу. Яку частину вантажу перевезли ці дві машини?

^{Короткий запис}

^{I — ?, 6/19 вантажу}

^{II — ?, 8/19 вантажу}

^{Разом — ?}

Розв’язання

6/19 + 8/19 = (6+8)/19 = 14/19 – частину вантажу перевезли дві машини.

Відповідь: дві машини перевезли 14/19 частину вантажу.

 

Вправи 806° Кіт Базиліо з’їв на обід 9/20 кг сосисок, а лисиця Аліса — на 3/20 кг більше, ніж Базиліо. Скільки кілограмів сосисок з’їли на обід Базиліо та Аліса разом?

^{Короткий запис}

^{Базіліо — 9/20 кг}

^{Аліса — ?, на 3/20 кг більше, ніж Базіліо}

^{Разом — ?}

Розв’язання

1) 9/20 + 3/20 = (9+3)/20 = 12/20 кг – сосисок з'їла лисиця Аліса.

2) 9/20 + 12/20 = (9 + 12)/20 = 21/20 кг – сосисок з'їли разом.

Відповідь: кіт Базиліо та лисиця Аліса разом з'їли 21/20 кг сосисок на обід.

 

Вправи 807° Вирушивши на прогулянку, черепаха Тортила за першу годину проповзла 23/50 км, що на 5/50 км більше, ніж за другу годину. Скільки кілометрів проповзла Тортила за дві години?

^{Короткий запис}

^{I — 23/50 кмб що на 5/50 км більше, ніж II}

^{II — ?}

^{Разом — ?}

Розв’язання

1) 23/50 – 5/50 = (23–5)/50 = 18/50 км – проповзла за другу годину.

2) 23/50 + 18/50 = (23+18)/50 = 41/50 км – проповзла за дві години разом.

Відповідь: за дві години Тортила проповзла 41/50 км.

 

Вправи 808 Розв’яжіть рівняння.

1) 52/63 – х/63 = 25/63    х/63 = 52/63 – 25/63    х/63 = (52–25)/63    х/63 = 27/63    х = 27	3) (12/13 + х) – 5/13 = 9/13 12/13 + х = 9/13 + 5/13 12/13 + х = (9+5)/13 12/13 + х = 14/13 х = 14/13 – 12/13 х = (14–12)/13 х = 2/13
2) х/38 + 14/38 = 23/38 х/38 = 23/38 – 14/38 х/38 = (23–14)/38 х/38 = 9/38 х = 9	4) (х – 21/31) + 14/31 = 25/31 х – 21/31 = 25/31 – 14/31 х – 21/31 = (25–14)/31 х – 21/31 = 11/31 х = 11/31 + 21/31 х = (11+21)/31 х = 32/31

Вправи 809 Розв’яжіть рівняння.

1) х/72 – 13/72 = 29/72    х/72 = 29/72 + 13/72    х/72 = (29+13)/72    х/72 = 42/72    х = 42	3) 15/17 – (b – 3/17) = 6/17 b – 3/17 = 15/17 – 6/17 b – 3/17 = (15–6)/17 b – 3/17 = 9/17 b = 9/17 + 3/17 b = (9+3)/17 b = 12/17
2) (29/42 – а) – 13/42 = 11/42 29/42 – а = 11/42 + 13/42 29/42 – а = (11+13)/42 29/42 – а = 24/42 а = 29/42 – 24/42 а = (29–24)/42 а = 5/42	4) 29/43 – (m + 13/43) = 5/43 m + 13/43 = 29/43 – 5/43 m + 13/43 = (29–5)/43 m + 13/43 = 24/43 m = 24/43 – 13/43 m = (24–13)/43 m = 11/43

Вправи 810 Овочевий магазин продав 240 кг картоплі. Першого дня було продано 3/16 картоплі, а другого дня — 7/16. Скільки кілограмів картоплі було продано за два дні?

^{Короткий запис}

^{Картоплі — 240 кг}

^{I — 3/16 від картоплі}

^{II — 7/16 від картоплі}

^{Разом — ?}

Розв’язання

1 спосіб

1) 3/16 + 7/16 = (3+7)/16 = 10/16 – частину картоплі продано за два дні.

2) 240 : 16 • 10 = 15 • 10 = 150 (кг) – картоплі продано за два дні.

2 спосіб

1) 240 : 16 • 3 = 45 (кг) – картоплі продано першого дня.

2) 240 : 16 • 7 = 105 (кг) – картоплі продано другого дня.

3) 45 + 105 = 150 (кг) – картоплі продано за два дні.

Відповідь: за два дні продано 150 кг картоплі. 

 

Вправи 811 Довжина побудованої дороги становить 92 км. За перший місяць побудували 6/23  дороги, а за другий місяць —  9/23. Скільки кілометрів дороги було побудовано за два місяці?

^{Короткий запис}

^{Дорога — 92 км}

^{I — 6/23 дороги}

^{II — 9/23 дороги}

^{Разом — ?}

Розв’язання

1 спосіб

1) 6/23 + 9/23 = 15/23 – частину дороги побудували за два місяці.

2) 92 : 23 • 15 = 60 (км) – дороги побудували за два місяці.

2 спосіб

1) 92 : 23 • 6 = 24 (км) – дороги побудували за перший місяць.

2) 92 : 23 • 9 = 36 (км) – дороги побудували за другий місяць.

3) 24 + 36 = 60 (км) – дороги побудували за два місяці.

Відповідь: за два місяці було побудовано 60 км дороги.

 

Вправи 812 Три трактористи зорали разом поле. Бригадир записав, що один із них зорав 5/13 поля, другий — 4/13, а третій — 6/13. Чи не помилився бригадир?

^{Короткий запис}

^{I — 5/13}

^{II — 4/13}

^{III — 6/13}

^{Разом — ?}

Розв’язання

5/13 + 4/13 + 6/13 = (5+4+6)/13 = 15/13 – частини поля.

15/13 ≠ 13/13 (13/13 = 1 — все поле)

Відповідь: бригадир помилився.

 

Вправи 813 Фермерка вирішила виділити під моркву 3/20 городу, під буряк — 4/20, під цибулю — 6/20, під горох — 2/20, під картоплю — 7/20. Чи зможе вона реалізувати свій план?

^{Короткий запис}

^{Морква — 3/20}

^{Буряк — 4/20}

^{Цибуля — 6/20}

^{Горох — 2/20}

^{Картопля — 7/20}

^{Разом — ?}

Розв’язання

3/20 + 4/20 + 6/20 + 2/20 + 7/20 = (3+4+6+2+7)/20 = 22/20 – частини поля.

22/20 ≠ 20/20 (20/20 = 1 — весь город)

Відповідь: не зможе.

 

Вправи для повторення

Вправи 814 За 200 г вафель заплатили 39 грн, а за 300 г печива — 63 грн. Що дорожче, 1 кг вафель чи 1 кг печива, і на скільки гривень?

Розв’язання

39 грн = 3900 к., 63 грн = 6300 к., 1 кг = 1000 г

1) 3900 : 200 • 1000 = 19500 (к.) = 195 (грн) – вартість 1 кг печива.

2) 6300 : 300 • 1000 = 21000 (к.) = 210 (грн) – вартість 1 кг вафлів.

3) 210 – 195 = 15 (грн) – на стільки дорожчий 1 кг печива.

Відповідь: на 15 грн дорожчий 1 кг печива, ніж вафель.

 

Вправи 815 Знайдіть усі натуральні числа, при діленні яких на 7 неповна частка дорівнюватиме остачі.

Розв’язання

^{Формула а = bq + r, q - неповна частка, r - остача. За умовою r=q=x, тому а = bх + х}

а : 7 = х (ост. х), причому х < 7  (остача менша від дільника)

а = 7х + х = 8х, причому х < 7 

При х = 1, а = 8 • 1 = 8

При х =2, а = 8 • 2 = 16

При х = 3, а = 8 • 3 = 24 

При х = 4, а = 8 • 4 = 32

При х = 5, а = 8 • 5 = 40

При х = 6, а = 8 • 6 = 48

Відповідь: 8, 16, 24, 32, 40, 48.

 

Задача від Мудрої Сови

Задача 816 У коробці лежать 4 білих, 5 чорних і 6 червоних кульок. Яку найменшу кількість кульок треба вийняти з коробки, щоб серед них обов’язково виявилося:

1) 3 кульки одного кольору. 

6 + 5 – 4 = 7 (к.) – найменша кількість кульок.

2) кульки всіх трьох кольорів.

Якщо витягнути 5 + 6 = 11 кульок, то серед них може не бути білої кульки, тому треба витягнути щонайменше 12 кульок.

 

---------------------------- у підручнику 2018 року --------------------------

Завдання 1 Порівняйте:

1) 18/29 > 15/29 ^{(більший дріб, у якого більший чисельник)}

2) 14/33 > 14/35 ^{(більший дріб, у якого менший  знаменник)}

3) 9/10 < 1 ^{(9/10 – правильний дріб, правильний дріб менший від 1)}

4) 10/9 > 1 ^{(1 = 9/9, більший дріб, у якого більший чисельник)}

5) 9/9 = 1 ^{(9/9 = 1, якщо чисельник дробу дорівнює знаменнику, то дріб дорівнює 1)}

6) 9/10 < 10/9 ^{(9/10 – правильний дріб, 10/9 – неправильний дріб, правильний дріб завжди менший від неправильного дробу)}

 

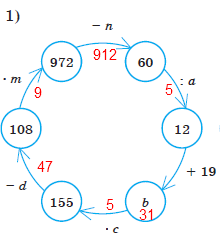
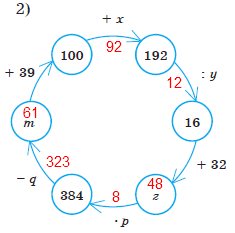
Вправи 759 Знайдіть числа, яких не вистачає в ланцюжку обчислень.

Інші завдання дивись тут ...