1) (−4,2 + 10) : (−0,2) = 5,8 : (−0,2) = −2,9
2) −20,4 − 4 + 0,2 = −24,4 + 0,2 = −24,2
Вправа 2 Ознаки подільності чисел
Щоб число 792* ділилося націло на 6, але не ділилося націло на 10, замість зірочки треба поставити цифру 6, отже, маємо число 7926
Вправа 3
Щоб число 1845* ділилося націло на 9, але не ділилося націло на 6, замість зірочки треба поставити цифру 9, отже, маємо число 18459.
Завдання 1255
Графік зміни температури повітря протягом доби.
1) О 4 год температура повітря –4°С, о 6 год — –5°С, о 10 год — –2°С, о 18 год — 5°С, о 22 год — 0°С;
2) Температура повітря 5°С була о 13 год та о 18 год, а –2°С — о 3 год, о 10 год та о 23 год;
3) Температура повітря була нульовою о 2 год, о 11 год та о 22 год.
4) Найнижча температура –5°С була о 6 год;
5) Найвища температура +7°С була о 16 год;
6) Температура повітря була нижчою від 0 °С з 2 год до 11 год та з 22 год до 24 год, а вищою за 0 °С — з 0 год до 2 год та з 11 год до 22 год;
7) Температура повітря підвищувалася з 6 год до 16 год, а знижувалася — з 0 год до 6 год та з 16 год до 24 год.
Завдання 1256
На рисунку зображено графік зміни температури повітря протягом доби.
1) О 2 год температура повітря була –5°С, о 8 год — –6°С, о 12 год — –4°С, о 16 — 0°С, о 22 год — –1°С.
2) Температура повітря була –3°С о 14 год, –6°С — о 3 год та о 8 год, 0°С — о 16 год та о 21 год;
3) Найнижча температура –10°С була о 6 год;
4) Найвища температура +4°С була о 19 год;
5) Температура повітря нижчою від 0°С була з 0 год до 16 год та з 21 год до 24 год, а вищою за 0°С — з 16 год до 21 год;
6) Температура повітря підвищувалася з 6 год до 19 год, а знижувалася — з 0 год до 6 год та з 19 год до 24 год.
Завдання 1257
На рисунку зображено графік зміни температури розчину під час хімічного досліду.
1) Початкова температура розчину +10°С;
2) Через 30 хв після початку досліду температура була 80°С, а через півтори години — 15°С;
3) Найвища температура розчину 45°С була через 60 хв після початку досліду;
4) Температура розчину 35°С була через 40 хв і через 70 хв після початку досліду.
Завдання 1258
Мотоцикліст виїхав з дому й через деякий час повернувся назад. У дорозі він двічі зупинявся для відпочинку. На рисунку зображено графік зміни відстані мотоцикліста від дому залежно від часу (графік руху мотоцикліста).
1) За першу годину руху мотоцикліст проїхав 60 км;
2) Першу зупинку від дому мотоцикліст зробив на відстані 120 км, другу зупинку — 75 км;
3) Перша зупинка тривала 1 год, друга зупинка — 30 хв;
4) Через 5 год після початку руху мотоцикліст був від дому на відстані 60 км;
5) Протягом останньої пів години мотоцикліст рухався зі швидкістю 45 км : 1/2 год = 45 • 2 = 90 км/год.
Завдання 1259
На рисунку 165 зображено графік руху туристки.
1) Через 10 год після початку руху туристка була на відстані 10 км;
2) Вона витратила на зупинку 3 год;
3) На відстані 8 км від дому туристка була через 2 год та через 11 год;
4) До зупинки туристка йшла зі швидкістю 16 км : 4 год = 4 км/год;
5) Протягом останніх двох годин туристка йшла зі швидкістю 6 км : 2 год = 3 км/год.
Завдання 1260
У таблиці наведено результати вимірювання температури повітря протягом доби через кожну годину.
|
Час доби, год
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
Температура, °С
|
2
|
3 | 1 | 0 | –2 | –3 | –5 | –4 | –2 | 0 | 1 | 4 | 7 |
|
Час доби, год
|
13
|
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|
Температура, °С
|
8
|
9 | 7 | 5 | 4 | 3 | 2 | 1 | 0 | –2 | –3 | –6 |
Графік зміни температури.
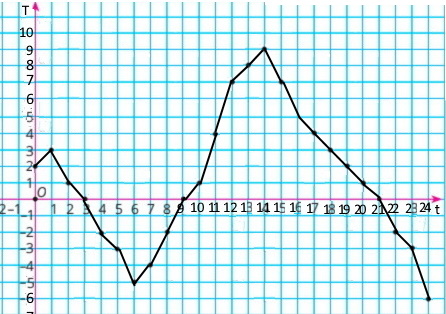
Температура підвищувалася з 0 год до 1 год та з 6 год до 14 год, а знижувалася з 1 год до 6 год та з 14 год до 24 год.
Завдання 1261
Велосипедист виїхав із дому на прогулянку. Спочатку він їхав 2 год зі швидкістю 12 км/год, потім відпочив годину і повернувся додому зі швидкістю 8 км/год.
Розв'язання
1) 12 • 4 = 24 (км) – проїхав зі швидкістю 12 км/год;
2) 24 : 8 = 3 (год) – проїхав зі швидкістю 8 км/год.
Таблиця залежності відстані від часу.
|
t
|
0
|
2
|
3
|
6
|
|
s
|
0
|
24
|
24 | 0 |
Графік руху велосипедиста.
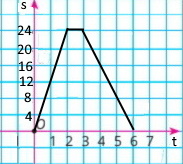
Завдання 1262, 1263 Побудуйте графіки функцій:
|
y = –2x
|
y = 3x
|
||||||||||||
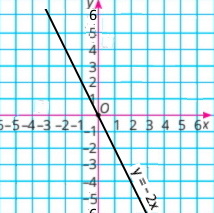 |
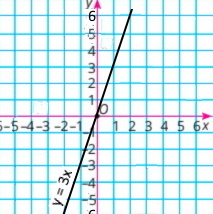 |
Вправи для повторення
Завдання 1264
Листоноша має 3 різних конверти і 4 різних поштових марки. Скільки в нього є варіантів вибору конверта з маркою?
Розв'язання
3 • 4 = 12 варіантів.
Відповідь: у листоноші є 12 варіантів вибору конвертів з маркою.
Завдання 1265
Василько прочитав 24% сторінок книжки, а потім ще 7/15 сторінок книжки. Після цього йому залишилося прочитати 44 сторінки. Скільки сторінок у книжці?
Розв'язання
Нехай в книжці х сторінок, тоді спочатку прочитав 0,24х сторінок, а потім — 7/15х сторінок. Складаємо рівняння:
х − 0,24х − 7/15х = 44
х − 6/25 х − 7/15х = 44
75/75 х − 18/75 х − 35/75 х = 44
22/75 х = 44
х = 44 : 22/75
х = 44 • 75/22
х = 150
Відповідь: у книзі 150 сторінок.
Завдання 1266 Вирази
1) Якщо a = −0,5, b = 2/3, тоді a : b – ab = −0,5 : 2/3 − (−0,5) • 2/3 =
−1/2 : 2/3 − (−1/2) • 2/3 = −1/2 • 3/2 + 1/3 = −3/4 + 1/3 = −9/12 + 4/12 = −5/12
2) якщо b = 2/7, c = −4/9, тоді (b + c)/(b − c) = (2/7 + (−4/9))/(2/7 − (−4/9)) =
= (2/7 − 4/9)/(2/7 + 4/9) = (18/63 − 28/63)/(18/63 + 28/63)) = −10/63 : 46/63 =
= −10/63 • 63/46 = −10/46 = −5/23
3) якщо x = −0,3, y = −0,4, тоді (x² + y²)/(x − y) = (−0,3² + (−0,4²))/(−0,3 − (−0,4)) =
= (0,09 + 0,16) : 0,1 = 0,25 : 0,1 = 2,5
Задача від Мудрої Сови
Завдання 1267
У кожну клітинку квадрата розміром 6 х 6 клітинок записали одне з чисел –1, 0, 1. Чи можуть суми чисел, які записані в кожному рядку, у кожному стовпчику і по двох великих діагоналях, бути різними? Не можуть. Кожна зі вказаних сум може приймати одне з 13 значень: –6; –4; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6. Усього сум 14 (6 рядків, 6 стовпців і 2 діагоналі). Отже, знайдуться дві рівні суми.
