ПРЯМА — це рівна лінія без початку і кінця.
Пряма є необмеженою.
Прямі проводять за допомогою лінійки, при цьому зображується тільки частина фігури.

Найчастіше прямі позначають малими латинськими буквами: a, b, c, d, k, l, m, n тощо.
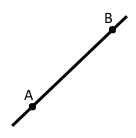
Пряму, на якій позначено дві точки, наприклад А, В, записують АВ або ВА (так позначати пряму дозволяє основна властивість прямої).
ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМОЇ І ТОЧКИ
◊ Аксіома. Яка б не була пряма є точки, які їй належать, та не належать.
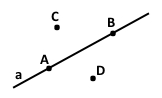
Кажуть: «точка А і В належить прямій а», «точка А і В лежить на прямій а», «пряма а проходить через точку А і В».
Записують А є а, B є а.
Кажуть: «точка C і D не належить прямій а», «точка С і D не лежить на прямій а», «пряма а не проходить через точку С і D».
Записують C ¢ а, D ¢ а.
◊ Аксіома. Основна властивість прямої. Через дві точки можна провести пряму і до того тільки одну.

Через дві точки можна провести багато різних кривих ліній, але пряма задається цими точками однозначно. У цьому й полягає суть основної властивості прямої.
◊ Через одну точку проходить безліч прямих.
Якщо прямі мають спільну точку, то кажуть, що вони перетинаються у тій точці.
◊ Аксіома. З трьох точок на прямій одна і тільки одна лежить між двома іншими.
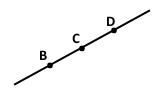
Якщо три точки лежать на одній прямій, тоді точка С лежить між точками В і D.
Наслідок. Якщо кажуть, що одна точка лежить між двома іншими, то ці три точки лежать на одній прямій.
ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХ
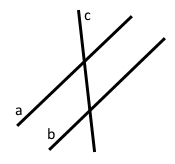
◊ Якщо дві прямі мають спільну точку, то вони перетинаються.
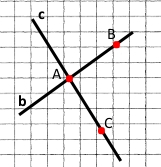
Точка А – спільна, вона належить обом прямим. А є b, А є c.
Прямі b і c перетинаються в точці А.
◊ Дві прямі на площині називають паралельними, якщо вони не перетинаються.

Прямі а і b паралельні, вони не перетинаються, тобто не мають жодної спільної точки.
Позначають а ǁ b.
Кажуть «пряма а є паралельна прямій b».