![]()
Серія "Вчимось разом" до підручника "Математика 3 клас Скворцова С.О., Онопрієнко О.В."
СТОРІНКА 97
Завдання 1
4) Складена задача на знаходження від’ємника
У ведмедика Пуха в шафі було 8 горнят меду. Після того як кілька горнят він сховав у погріб, у шафі залишилась 1/4 запасів. Скільки горнят меду ведмедик сховав у погріб?
|
Було |
Сховав |
Залишилося |
|
8 горнят |
? |
1/4 від було |
Короткий запис
Було — 8 горнят
Сховав — ?
Залишилось — ?, 1/4 від було
Схема
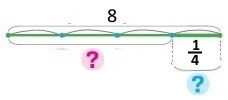
Вираз 8 – 8 : 4
|
Короткий запис №1 Залишилось — ?, 1/4 від 8 горнят |
Короткий запис №2 Було — 8 горнят Сховав — ? Залишилось — 2 горнята |
План розв’язування
1) Скільки горнят меду залишилось у шафі?
2) Скільки горнят меду ведмедик заховав у погріб?
Розв’язання
1) 8 : 4 = 2 (г.) – горнят меду ведмедик залишив у шафі
2) 8 – 2 = 6 (г.) – горнят меду ведмедик сховав у погріб
Відповідь: у погріб ведмедик сховав 6 горнят меду
5) Складена задача на збільшення на частину числа
Ведмедик Пух планував з'їсти за місяць 8 горнят меду, а з'їв на 1/4 горнят більше, ніж запланував. Скількома горнятами меду поласував ведмедик упродовж місяця?
Короткий запис
Планував — 8 горнят
З’їв — ?, на ? (1/4 планував) горнят більше
Схема
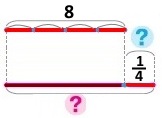
Вираз 8 + 8 : 4
|
Короткий запис №1 Планував — 8 горнят Більше — ?, 1/4 планував |
Короткий запис №2 З’їв — ?, на 2 горнята більше |
План розв’язування
1) На скільки більше з'їв, ніж планував?
2) Скількома горнятами меду поласував ведмедик упродовж місяця?
Розв’язання
1) 8 : 4 = 2 (г.) – на стільки більше з’їв, ніж планував
2) 8 + 2 = 10 (г.) – горнятами меду поласував ведмедик упродовж місяця
Відповідь: протягом місяця поласував 10 горнятами меду
Завдання 2
Якщо доданок збільшити (зменшити) на деяке число, то сума збільшиться (зменшиться) на таке саме число.
Якщо множник збільшити (зменшити) у декілька разів, то добуток збільшиться (зменшиться) у стільки ж разів.
|
36 + 30 = 66 36 + 27 = 36 + 24 + 3 = 63 30 > 27 на 3 66 > 63 на 3 |
3 • 2 = 6 3 • 4 = 12 2 < 4 у 2 рази 6 < 12 у 2 рази |
8 • 3 = 24 2 • 3 = 6 8 > 2 у 4 рази 24 > 6 у 4 рази |
2 спосіб
36 + 30 = 66
36 + 27 = 36 + (30 – 3) = (36 + 30) – 3 = 66 – 3 = 63
3 • 2 = 6
3 • 4 = 3 • (2 • 2) = (3 • 2) • 2 = 6 • 2 = 12
8 • 3 = 24
2 • 3 = (8 : 4) • 3 = (8 • 3) : 4 = 24 : 4 = 6
Завдання 3 Рівняння
|
54 – х = 38 х = 54 – 38 х = 16 54 – 16 = 38 38 = 38 |
а • 4 = 32 а = 32 : 4 а = 8 8 • 4 = 32 32 = 32 |
64 : р = 8 р = 64 : 8 р = 8 64 : 8 = 8 8 = 8 |
с : 7 = 4 с = 4 • 7 с = 28 28 : 7 = 4 4 = 4 |
|
54 – х = 38 54 – х = 54 – 16 х = 16 |
а • 4 = 32 а • 4 = 8 • 4 а = 8 |
64 : р = 8 64 : р = 64 : 8 р = 8 |
с : 7 = 4 с : 7 = 28 : 7 с = 28 |
Завдання 4 Порядок дій
80 – 5 • 9 + 38 = 80 – 45 + 38 = 35 + 38 = 73
100 – 29 + 28 : 4 = 100 – 29 + 7 = 71 + 7 = 78
(53 – 29) : 4 = (53 – 23 – 6) : 4 = 24 : 4 = 6
32 : 8 • 7 = 4 • 7 = 28 24 : 6 + 48 = 4 + 48 = 52
27 – 19 + 7 • 7 = 27 – 19 + 49 = 8 + 49 = 57
СТОРІНКА 98
Завдання 1
Якщо від’ємник збільшити (зменшити) на деяке число, то різниця зменшиться (збільшиться) на таке саме число.
Якщо дільник збільшити (зменшити) у декілька разів, то частка зменшиться (збільшиться) у стільки ж разів.
Якщо ділене збільшити (зменшити) на деяке число, то частка збільшиться (зменшиться) у стільки ж разів.
|
12 – 2 = 10 12 – 5 = 7 2 < 5 на 3 10 > 7 на 3 |
12 : 2 = 6 12 : 4 = 3 2 < 4 у 2 рази 6 > 3 у 2 рази |
9 : 3 = 3 18 : 3 = 6 9 < 18 у 2 рази 3 < 6 у 2 рази |
2 спосіб
12 – 2 = 10
12 – 5 = 12 – (2 + 3) = 12 – 2 – 3 = 10 – 3 = 7
12 : 2 = 6
12 : 4 = 12 : (2 • 2) = (12 : 2) : 2 = 6 : 2 = 3
9 : 3 = 3
18 : 3 = (9 • 2) : 3 = (9 : 3) • 2 = 3 • 2 = 6
Завдання 2 Замінили кожний дріб часткою двох натуральних чисел:
1/7 = 1 : 7 1/9 = 1 : 9 1/12 = 1 : 12 1/100 = 1 : 100
Дроби в порядку зростання (від меншого до більшого): 1/100, 1/12, 1/9, 1/7
Як змінюється знаменник — дільник? Зменшується.
Як змінюється дріб — частка? Збільшується.
Завдання 3
1/9 від 63 = 63 : 9 = 6
ціле, якщо його 1/6 дорівнює 8, тоді 8 • 6 = 48
1/4 від 32 = 32 : 4 = 8
Завдання 4
1) Проста задача на знаходження частини числа
Щоб приготувати варення, кухар узяв сливи і цукор. Слив було 8 кг, а маса цукру становила половину маси слив. Скільки кілограмів цукру взяв кухар?
Короткий запис
Сливи — 8 кг
Цукор — ?, 1/2 слив
Схема
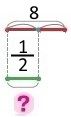
Розв’язання
8 : 2 = 4 (кг) – кілограмів цукру взяв кухар
Відповідь: кухар взяв 4 кілограми цукру
2) Складена задача на знаходження суми
Щоб приготувати варення, кухар узяв сливи і цукор. Слив було 8 кг, а маса цукру становила половину маси слив. Скільки всього кілограмів слив і цукру взяв кухар?
|
Сливи |
Цукор |
Всього |
|
8 кг |
половина слив |
? |
Короткий запис
Сливи — 8 кг
Цукор — ?, половина слив
Всього — ?
Схема
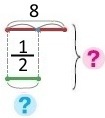
Вираз 8 + (8 : 2)
|
Короткий запис №1 Сливи — 8 кг Цукор — ?, половина слив |
Короткий запис №2 Цукор — 4 кг Всього — ? |
План розв’язування
1) Скільки кілограмів цукру взяв кухар?
2) Скільки всього кілограмів слив і цукру взяв кухар?
Розв’язання
1) 8 : 2 = 4 (кг) – кілограмів цукру взяв кухар
2) 8 + 4 = 12 (кг) – всього кілограмів слив і цукру взяв кухар
Відповідь: кухар взяв 12 кілограмів слив і цукру
Змінили запитання так, щоб в її розв'язанні останньою була дія віднімання.
Складена задача на різницеве порівняння. Щоб приготувати варення, кухар узяв сливи і цукор. Слив було 8 кг, а маса цукру становила половину маси слив.
|
На скільки більше кілограмів слив, ніж цукру, взяв кухар? Короткий запис Сливи — 8 кг; на ? більше Цукор — ?, половина слив |
На скільки кілограмів менше цукру, ніж слив, узяв кухар? Короткий запис Сливи — 8 кг Цукор — ?, половина слив; на ? менше |
СТОРІНКА 99
Завдання 5
1) Складена задача на різницеве порівняння
Для настилання підлоги привезли 42 соснові дошки, а смерекових дошок — у 7 разів менше. На скільки більше привезли соснових дошок, ніж смерекових?
Короткий запис
Соснові — 42 дошки; на ? дошок більше
Смерекові — ?, у 7 разів менше
Схема
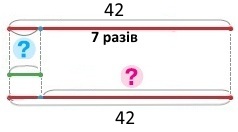
Вираз 42 – 42 : 7
|
Короткий запис №1 Соснові — 42 дошки Смерекові — ?, у 7 разів менше |
Короткий запис №2 Соснові — 42 дошки, на ? дошок більше Смерекові — 6 дошок |
План розв’язування
1) Скільки привезли смерекових дошок?
2) На скільки більше привезли соснових дошок, ніж смерекових?
Розв’язання
1) 42 : 7 = 6 (д.) – смерекових дошок привезли
2) 42 – 6 = 36 (д.) – на стільки більше привезли соснових дошок, ніж смерекових
Відповідь: привезли на 9 дошок більше соснових, ніж смерекових
2) Складена задача на різницеве порівняння
Для настилання підлоги привезли дошки — смерекові і 42 соснові. Кількість смерекових дошок становила 1/7 від соснових. На скільки більше привезли соснових дошок, ніж смерекових?
Короткий запис
Соснові — 42 дошки; на ? дошок більше
Смерекові — ?, 1/7 соснових
Схема
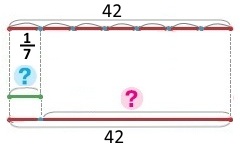
Вираз 42 – 42 : 7
|
Короткий запис №1 Соснові — 42 дошки Смерекові — ?, 1/7 соснових |
Короткий запис №2 Соснові — 42 дошки, на ? дошок більше Смерекові — 6 дошок |
План розв’язування
1) Скільки привезли смерекових дошок?
2) На скільки більше привезли соснових дошок, ніж смерекових?
Розв’язання
1) 42 : 7 = 6 (д.) – смерекових дошок привезли
2) 42 – 6 = 36 (д.) – на стільки більше привезли соснових дошок, ніж смерекових
Відповідь: привезли на 9 дошок більше соснових, ніж смерекових
Завдання 6 Яких значень може набувати змінна с, щоб дріб 1/с був більшим за 1/8?
Серед дробів з однаковими чисельниками у більшого дробу менший знаменник, тому
с < 8
Завдання 7 До невідомого числа додали добуток чисел 6 і 7 та одержали результат, що дорівнює сумі чисел 37 і 45
х + 6 • 7 = 37 + 45
х + 42 = 37 + 3 + 42
х + 42 = 40 + 42
х = 40
2 спосіб
х + 6 • 7 = 37 + 45
х + 42 = 82
х = 82 – 42
х = 40