Комбінована контрольна робота 10. Варіант 1
Завдання 1.
34 048 : (407 • 34 – 13 782) = 608
|
х 407 34 1628 1221 13838 |
_13838 13782 56 |
_34048 | 56 336 608 _448 448 0 |
Завдання 2. Іменовані числа в порядку спадання.
32 ц 70 кг, 3 т 2 ц 7 кг, 3 т 27 кг
Міркуємо так.
1 спосіб
Зведемо всі числа до найменшої одиниці вимірювання (кг), тоді
3 т 27 кг = 3 • 1000 кг + 27 кг = 3027 кг
3 т 2 ц 7 кг = 3 • 1000 кг + 2 • 100 кг + 7 кг = 3207 кг
32 ц 70 кг = 32 • 100 кг + 70 кг = 3270 кг
У порядку спадання маємо числа: 3270 кг, 3207 кг, 3027 кг
2 спосіб
3 т 27 кг
3 т 2 ц 7 кг
32 ц 70 кг = 30 ц + 2 ц + 70 кг = 3 т 2 ц 70 кг
У порядку спадання маємо числа: 3 т 2 ц 70 кг, 3 т 2 ц 7 кг, 3 т 27 кг
Завдання 3. Рівняння.
у : (5400 : 90) = 120
у : (540 : 9) = 120
у : 60 = 120
у = 120 • 60
у = 7200
Завдання 4. Олег спостерігав, як рухалася мураха вздовж олівця довжиною 270 мм. Цю відстань вона подолала за 6 с. А потім сонечко пройшло цей шлях за 30 с. На скільки швидкість мурахи більша за швидкість сонечка?
Розв’язання
1 спосіб
1) 270 : 6 = 45 (мм/с) — швидкість мурахи.
2) 270 : 30 = 9 (мм/с) — швидкість сонечка.
3) 45 – 9 = 36 (мм/с) — на стільки більша швидкість мурахи, ніж сонечка.
2 спосіб
1) 270 : 6 = 45 (мм/с) — швидкість мурахи.
2) 30 : 6 = 5 (разів) — у стільки разів повільніша швидкість сонечка.
3) 45 : 5 = 9 (мм/с) — швидкість сонечка.
4) 45 – 9 = 36 (мм/с) — на стільки більша швидкість мурахи, ніж сонечка.
Відповідь: на 36 мм/с більша швидкість мурахи, ніж сонечка.
Завдання 5. Костику для аплікації треба вирізати прямокутник, ширина якого — 3 см, а довжина — у 2 рази більша. Побудуй прямокутник, який треба вирізати Костику, та обчисли його периметр.
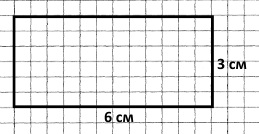
Розв’язання.
1) 3 • 2 = 6 (см) — довжина прямокутника.
2) Р = (3 см + 6 см) • 2 = 18 (см) — периметр прямокутника.
Відповідь: 18 см периметр прямокутника.
Завдання 6. У класі навчається 11 хлопчиків та 15 дівчаток. Половина учнів класу бере участь у конкурсі «Найрозумніший». Яка найменша кількість дівчаток може взяти участь у конкурсі?
Розв'язання.
1) 11 + 15 = 26 (уч.) – всього учнів навчається у класі.
2) 26 : 2 = 13 (уч.) – учнів беруть участь у конкурсі.
3) 13 – 11 = 2 (д.) – найменша кількість дівчаток може взяти участь у конкурсі.
Відповідь: 2 дівчинки щонайменше можуть взяти участь у конкурсі.
Комбінована контрольна робота 10. Варіант 2
Завдання 1.
27 807 : (508 • 37 – 18 727) = 403
|
х 508 37 3556 1524 18796 |
_18796 18727 69 |
_27807 | 69 276 403 _207 207 0 |
Завдання 2. Іменовані числа в порядку спадання.
43 002 мм, 43 дм 2 см, 4 м 30 см 2 мм
Міркуємо так.
1 спосіб
Зведемо усі величини до найменшої одиниці вимірювання (мм).
43 дм 2 см = 43 • 10 см + 2 см =430 см + 2 см = 432 см = 4320 мм
43 002 мм
4 м 30 см 2 мм = 4000 мм + 300 мм + 2 мм = 4302 мм
Маємо в порядку спадання 43002, 4320, 4302
2 спосіб
43 дм 2 см
43 002 мм = 43000 мм + 2 мм = 430 дм 2 мм
4 м 30 см 2 мм = 4 м + 30 см + 2 мм = 40 дм + 3 дм + 2 мм = 43 дм 2 мм
Маємо в порядку спадання 430 дм 2 мм, 43 дм 2 см, 43 дм 2 мм
Завдання 3. Рівняння
k • (6400 : 80) = 2400
k • (640 : 8) = 2400
k • 80 = 2400
k = 2400 : 80
k = 30
Завдання 4. За 5 хв комар пролетів 155 м, а муха за 7 хв — 364 м. На скільки швидкість комара менша за швидкість мухи?
Розв’язання
1) 155 : 5 = 31 (м/хв) — швидкість комара.
2) 364 : 7 = 52 (м/хв) — швидкість мухи.
3) 52 – 31 = 21 (м/хв) — на стільки менша швидкість комара за швидкысть мухи.
Відповідь: на 21 м/хв менша швидкість комара за швидкысть мухи.
Завдання 5. Підковдру для лялькової ковдри прямокутної форми потрібно оздобити тасьмою. Довжина ковдри — 11 см, а ширина — на 5 см менша. Побудуй прямокутник, який буде викрійкою, та визнач, скільки сантиметрів тасьми потрібно для оздоблення підковдри по її периметру.
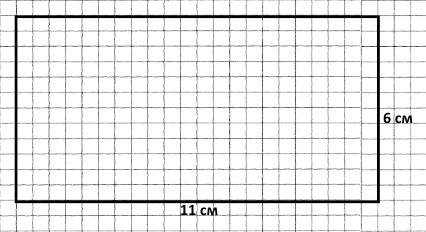
Розв’язання
1) 11 – 5 = 6 (см) — ширина підковдри.
2) Р = (11 см + 6 см) • 2 = 34 см — довжина тасьми для оздоблення.
Відповідь: 34 см тасьми потрібно для оздоблення підковдри по її периметру.
Завдання 6. У 4–А класі навчається 14 дівчаток, а в 4–Б класі — 18. Половина всіх четвертокласниць узяла участь у конкурсі «Міс школи». Яка найменша кількість дівчаток 4–Б класу могла взяти участь у конкурсі?
Розв'язання.
1) 14 + 18 = 32 (уч.) – усього учнів в 4-х класах.
2) 32 : 2 = 16 (уч.) – учнів взяли участь у конкурсі.
3) 16 – 14 = 2 (д.) – найменша кількість дівчаток 4–Б класу могла взяти участь у конкурсі.
Відповідь: 2 дівчинки 4-Б класу щонайменше могли взяти участь у конкурсі.