Інші завдання дивись тут...

© Барна Р., 2021   

Серія "Вчимось разом" до робочого зошита "Математика 4 клас Лишенко Г."

Сторінка 87

Завдання 6 Складена задача на ділення на вміщення

Двома сівалками за 5 год засіяли кукурудзою 120 га. За скільки годин такою сівалкою можна засіяти кукурудзою 84 га?

Площа за 1 год 1 сівалка (га)	Кількість год	Кількість сівалок	Загальна площа (га)
?	5	2	120
однакова	?		84

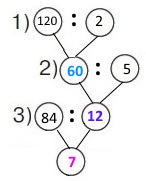
^{Вираз          84 : (120 : 2 : 5)}

Розв’язання

1) 120 : 2 = 60 (га) – площу засіє 1 сівалка за 5 год.

2) 60 : 5 = (50 + 10) : 5 = 12 (га) – площу засіє 1 сівалка за 1 год.  

3) 84 : 12 = 7 (год) – годин можна засіяти.  

Відповідь: можна засіяти за  7 годин.  

Завдання 7 Письмове ділення

Відновили пропущені цифри:

_9***| 3*  *6      ***   _2*4     ***        0

_9824| 32   96       307   _224     224          0

_6*8|  *4   **    *7 _16*   ***       0

_648| 24   48     27 _168   168       0

_* * * *|  * 5  * 7 *      2 *   _5 9 *     * * *          0

_2295| 85   170    27   _595     595         0

До № 662 – 681

Завдання 1 

Письмове ділення перевірили письмовим множенням

_7368 |  24   72      307  _168    168        0

х307    24 1228 614 7368

_310140 |   45   270        6892   _401     360     _414       405         _90           90             0

х  6892        45   34460 27568 310140

Сторінка 88

Завдання 2

Автомобіль першого дня проїхав 480 км, а другого — 2/3 того, що проїхав першого дня. На кожні 100 км шляху він витрачав 9 л бензину. Скільки всьо­го літрів бензину витратив автомобіль за два дні?

Короткий запис №1 І день — 480 км ІІ день — ?, 2/3 від І дня

Короткий запис №2 І день — 480 км ІІ день — 320 км Всього — ?

Короткий запис №3 9 л — 100 км ? л — 800 км, у ? разів більше

Розв'язання

1) 480 : 3 • 2 = 320 (км) – відстань проїхав автомобіль ІІ дня.

2) 480 + 320 = 800 (км) – відстань проїхав автомобіль за два дні.

3) 800 : 100 = 8 (р.) – у стільки разів більша відстань.

4) 8 • 9 = 72 (л) – літрів бензину витратив автомобіль.

Відповідь: автомобіль витратив 72 літри бензину.

Завдання 3

Ділянку прямокутної форми довжиною 100 м і шириною 80 м треба обнести парканом. 3 робітники за 5 год спорудили 180 м паркану. За скільки днів один робітник завершить роботу, якщо працюватиме з такою самою продуктивністю праці?

Довжина за 1 год 1 робітник (м)	Кількість год	Кількість робітників	Загальна довжина (м)
?	3	5	180
однакова	?		?, Р – 180

Розв’язання

1) Р = 100 • 2 + 80 • 2 = 360 (м) – довжина паркану.

2) 180 : 3 = 60 (м) – метрів паркану кладе 1 робітник за 5 год.

3) 60 : 5 = 12 (м) – метрів паркану кладе 1 робітник за 1 год.

4) 360 – 180 = 360 – 200 + 20 = 180 (м) – метрів залишилося обнести парканом.

5) 180 : 12 = 180 : 6 : 2 = 15 (год) – годин.

Відповідь: робітник завершить роботу за 15 годин.

До № 682 – 702

Завдання 1 Одиниці вимірювання

8 т З0 кг = 8000 кг + 30 кг = 8030 кг З год 20 хв = 60 хв • 3 + 20 хв = 200  хв 5 км 80 м = 5000 м + 80 м = 5080 м

З год : 18 = 180 хв : 18 = 10  хв 4 кг : 80 = 4000 г : 80 = 400 г : 8 = 50 г 7 ц : 14 = 700 кг : 14 = 700 кг : 7 : 2 = 50 кг

Сторінка 89

Завдання 2

_3744 |   18   36       208   _144     144         0

х208    18 1664 208 3744

_970582 |   97   97          10006      _582        582            0

х10006        97   70042 90054 970582

Завдання 3 Складена задача на знаходження суми

Для сівби на одне поле привезли 45 мішків пшени­ці, а на друге — 69 мішків такої самої маси. На друге поле привезли пшениці на 1 т 920 кг більше, ніж на перше. Скільки всього кілограмів пшениці привезли на обидва поля?

Поле	Маса 1 мішка (кг)	Кількість мішків	Загальна маса пшениці (кг)
І	однаково	45
ІІ	?	69, на ? мішків більше	на 1920 кг більше
Разом	однаково	?	?

Розв'язання

1 т 920 кг = 1000 кг + 920 кг = 1920 кг

1) 69 – 45 = 24 (м.) – на стільки більше мішків пшениці привезли на ІІ поле.

2) 1920 : 24 = 80 (кг) – кілограмів пшениці в одному мішку.

3) 45 + 69 = 114 (м.) – всього мішків пшениці привезли.

4) 80 • 114 = 9120 (кг) – всього кілограмів пшениці привезли на два поля.

^{2 спосіб}

^{1) 69 – 45 = 24 (м.) – на стільки більше мішків пшениці привезли на ІІ поле.}

^{2) 1920 : 24 = 80 (кг) – кілограмів пшениці в одному мішку.}

^{3) 45 • 80 = 3600 (кг) – кілограмів пшениці привезли на І поле.}

^{4) 69 • 80 = 5520 (кг) – кілограмів пшениці привезли на ІІ поле.}

^{5) 3600 + 5520 = 9120 (кг) – всього кілограмів пшениці привезли на два поля.}

Відповідь: привезли 9120 кілограмів.

Завдання 4

Лісник ділянку лісу прямокутної форми довжиною 4 км і шириною 2 км може обійти за З год. За скільки годин ліс­ник об'їде цю ділянку на велосипеді, якщо їхатиме у З рази швидше, ніж іде пішки?

Розв’язання

1) Р = (4 + 2) • 2 = 12 (км) – периметр треба обійти.

2) 12 : 3 = 4 (км/год) – швидкість пішки.

3) 4 • 3 = 12 (км/год) – швидкість на велосипеді.

4) 12 : 12 = 1 (год) – годин на дорогу.

Відповідь: об'їде цю ділянку на велосипеді за 1 годину.

 

Сторінка 90

Завдання 5

Чи завжди сума чотирицифрового числа й одноцифрового числа більша, ніж сума двох трицифрових чисел? Доведи.

^{Наприклад, сума найменшого чотирицифрового числа і найменшого одноцифрового числа менша від суми двох найбільших трицифрових чисел.}

1000 + 1 = 1001

999 + 999 = 1998

1001 < 1998

Ні.

До № 703 – 722

Завдання 1

235 • 101 = 235 • 100 + 235 = 23500 + 235 = 23735

267 • 99 = 267 • 100 – 267 = 26700 – 267 = 26700 – 300 + 33 = 26433

128 • 999 = 128 • 1000 – 128 = 128 000 – 128 = 128 000 – 200 + 72 = 127 872

1323 • 11 = 1323 • 10 + 1323 = 13230 + 1323 = 10000 + 4000 + 500 + 50 + 3 = 14553

2678 • 9 = 2678 • 10 – 2678 = 26780 – 2678 = 24780 – 678 = 24102

Завдання 2

11 т 564 кг : 49 – 5 т 696 кг : 32 = 58 кг

_11564|  49     98      236 (кг)  _176    147    _294      294         0

_5696|   32   32      178 (кг) _249   224  _256    256        0

_236   178    58 (кг)

Сторінка 91

Завдання 3

Знайди площу ділянки за планом.

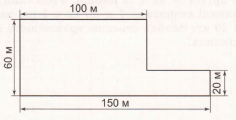
Розв'язання

1) 150 • 60 = 9000 (м2) – площа великого прямокутника.

2) (150 – 100) • (60 – 20) = 50 • 40 = 2000 (м²) – частина площі, яку треба відкинути.

3) 9000 – 2000 = 7000 (м²) – шукана площа.

^{2 спосіб}

_{1) 100 • 60 = 6000 (м²) – площа першої частини.}

_{2) (150 – 100) • 20 = 1000 (м²) – площа другої частини.}

_{3) 6000 + 1000 = 7000 (м²) – шукана площа.}

Відповідь: площа ділянки 7000 м².

Завдання 4 Складена задача на знаходження чисел за трьома сумами

Для опалення школа за З зимових місяці витратила 7 т 2 ц (7 т 200 кг) ву­гілля. За грудень і січень — 5 т 140 кг, за січень і лютий — 5 т 440 кг. Скільки вугілля витрачали на опалення щомісяця?

^{Короткий запис}

^{Грудень і січень — 5 т 140 кг}

^{Січень і лютий — 5 т 440 кг}

^{Всього грудень, січень, лютий — 7 т 200 кг}

^{Грудень — ?  Січень — ?  Лютий — ?}

Розв’язання

^{7 т 2 ц = 1 т • 7 + 1 ц • 2 = 1000 кг • 7 + 100 кг • 2 = 7200 кг}

^{5 т 140 кг = 1 т • 5 + 140 кг = 1000 кг • 5 + 140 кг = 5140 кг}

^{5 т 440 кг = 1 т • 5 + 440 кг = 1000 кг • 5 + 440 кг = 5 440 кг}

1) 7200 – 5440 = 7200 – 6000 + 560 = 1760 (кг) = 1 т 760 кг – витратили у грудні.  

2) 5140 – 1760 = 5140 – 2000 + 240 = 3380 (кг) = 3 т 380 кг – витратили у січні.

3) 5440 – 3380 = 5440 – 4000 + 620 = 2060 (кг) = 2 т 60 кг – витратили в лютому.

2 спосіб

1)  7 т 200 кг    _6 т1200 кг      5 т 440 кг      1 т 760 кг – витратили у грудні.

2) 5 т 140 кг   _4 т1140 кг     1 т  760 кг     3 т 380 кг – витратили у січні.

3) 5 т 440 кг     3 т 380 кг     2 т 060 кг – витратили в лютому.

Відповідь: у грудні витратили 1 т 760 кг, у січні – 3 т 380 кг, у лютому – 2 т 60 кг.

Завдання 3

У змаганнях з волейболу брали участь 16 команд. Команда, яка програвала, вибувала з  гри. Скільки всього відбулося ігор?

^{Примітка. Найбільшого поширення набули три способи проведення змагань: перший – коловий, коли всі команди, що беруть участь, проводять ігри між собою незалежно від результату окремих зустрічей; другий – з вибуванням із змагань після програшу зустрічі, коли команда після програшу однієї або двох зустрічей в подальших іграх вже не бере участь; третій – змішаний, коли перша частина змагання проводиться з вибуванням, а друга – за коловим способом, або навпаки. У способі з вибуванням у міру проведення змагання на кожну нову стадію змагань виходять сильніші команди, і так аж до фіналу.}

^{Міркуємо так. Таку задачу можна розв’язати, якщо припустити, що не було нічийного рахунку. Після того як попарно зіграють 16 команд, маємо 8 ігор, переможцями залишаться 8 команд. Після того як попарно зіграють 8 команд, маємо ще 4 ігри, переможцями залишаться 4 команди. Після того як попарно зіграють 4 команд, маємо ще 2 ігри, переможцями залишаться 2 команди. Після того як попарно зіграють 2 команди,  маємо ще 1 гру, переможцем залишиться 1 команда.}

8 + 4 + 2 + 1 = 15 (іг.) – щонайменше ігор треба провести.

  

Сторінка 92 До № 723 – 743

Завдання 1

Постав дужки так, що рівності були істинними.

(240 : 40+ 20) • 2 = (6 + 20) • 2 = 26 • 2 = 26 + 26 = 52 240 : (40 + 20) • 2 = 240 : 60 • 2 = 4 • 2 = 8 240 : (40 + 20 • 2)= 240 : (40 + 40) = 240 : 80 = 3

(90 – З0 : 3) • 5 = (90 – 10) • 5 = 80 • 5 = 400 (90 – З0) : 3 • 5 = 60 : 3 • 5 = 20 • 5 = 100 90 – З0 : (3 • 5) = 90 – 30 : 15 = 90 – 2 = 88

Завдання 2

В одному баку було 160 л води, а в другому — 190 л. Скільки літрів води треба перелити з другого баку в перший, щоб в обох баках стало води порів­ну? 

Розв'язання

1) 160 + 190 = 160 + 40 + 150 = 350 (л) – всього літрів води було у двох баках.

2) 350 : 2 = (200 + 140 + 10) : 2 = 175 (л) – літрів води стало в кожному баці (порівну).

3) 190 – 175 = 15 (л) – літрів води треба перелити з другого баку в перший.

^{2 спосіб}

1) 190 – 160 = 30 (л) – на стільки літрів води більше у другому баку, ніж у першому.

2) 30 : 2 = 15 (л) – літрів води треба перелити з другого баку в перший.

^{3 спосіб}

^{Нехай х (л) – літрів треба перелити, тоді 160 + х (л) – літрів стане в І баці, 190 – х (л) – літрів стане в ІІ баці. Складемо рівняння.}

^{(160 + х) – (190 – х) = 0}

^{160 + х – 190 + х = 0}

^{2 • х – 30 = 0}

^{2 • х = 0 + 30}

^{2 • х = 30}

^{х = 30 : 2 = 15 (л)}

Відповідь: треба перелити 15 літрів води.

Завдання 3

Знайди площу ділянки навколо басейну за планом.

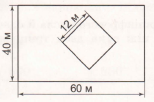
Розв'язання

1) 60 • 40 = 2400 (м²) – площа прямокутника довжиною 60 м і шириною 40 м.

2) 12 • 12 = 144 (м²) – площа квадрата зі стороною 12 м.

3) 2400 – 144 = 2400 – 200 + 56 = 2256 (м²) – шукана площа.

Відповідь: площа ділянки навколо басейну 2256 м².

Завдання 4

Зі стосу із роздрукованим текстом випала частина сторінок. Перша сторінка цієї частини має номер 25, а номер останньої сторінки позначено тими самими цифрами, але в зворотному порядку. Скільки сторі­нок випало зі стосу?

^{Міркуємо так. Випали сторінки  із 25 по 52 включно. Їх кількість шукаємо за відомою формулою.}

52 – 25 + 1 = 28 (стор.)

Відповідь: зі стосу випало 28 сторінок.

 

Сторінка 93

Завдання 5

_12282 | 534  1068       23  _1602    1602         0

х  534      23   1602 1068 12282

_723168 |  243  486         2976 _2371  2187  _1846    1701    _1458      1458            0

х  2976      243     8928  11904  5952  723168

До № 744 – 764

Завдання 1

736 200 : 18 – 640 096 : 32 + 1 948 = 22 845

_736200 |     18   72         40900   _162     162         0

_640096 |   32   64         20003        _96          96            0

_40900   20003   20897

+20897     1948    22845

Завдання 2

Виконай обчислення за схемою, підставивши за­мість а число з таблиці. Отримані результати запи­ши в таблицю.

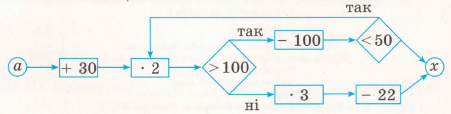
a	10	25	6	50	100	30
x	218	38	194	60	160	98
букви	Б	К	М	О	У	Л

^{10 + 30 = 40       40 • 2 = 80         80 • 3 = 240            240 – 22 = 218}

^{25 + 30 = 55       55 • 2 = 110       110 – 100 = 10        10 • 2 = 20    20 • 3 = 60     60 – 22 = 38}

^{6 + 30 = 36         36 • 2 = 72         72 • 3 = 216            216 – 22 = 194}

^{50 + 30 = 80       80 • 2 = 160       160 – 100 = 60}    

^{100 + 30 = 130   130 • 2 = 260      260 – 100 = 160}

^{30 + 30 = 60       60 • 2 = 120       120 – 100 = 20         20 • 2 = 40    40 • 3 = 120   120 – 22 = 98}

 

Сторінка 94

*Розташуй значення х у порядку збільшення і дізнай­ся прізвище мореплавця, першовідкривача Південної Америки.

X	38	60	98	160	194	218
букви	К	О	Л	У	М	Б

Завдання 3 Складена задача на знаходження суми

Щоб викачати воду з баржі задіяли два однакових насоси. Перший працював 10 хв, а другий — 15 хв. Скільки літрів води викачали насоси, якщо другий викачав на 250 л більше, ніж перший?

Насос	Літрів за 1 хв	Кількість хв	Загальна кількість літрів
І	однаково	10
ІІ	?	15, на ? л більше	на 250 л більше
Разом	однаково	?	?

Розв'язання

1) 15 – 10 = 5 (хв.) – на стільки більше хвилин працював ІІ насос.

2) 250 : 5 = 50 (л) – літрів води викачує кожний насос за 1 хвилину.

3) 15 + 10 = 25 (хв.) – всього хвилин працювали насоси.

4) 50 • 25 = 1250 (л) – літрів води викачали два насоси.

^{2 спосіб}

^{1) 15 – 10 = 5 (хв.) – на стільки більше хвилин працював ІІ насос.}

^{2) 250 : 5 = 50 (л) – літрів води викачує кожний насос за 1 хвилину.}

^{3) 50 • 10 = 500 (л) – літрів води викачав І насос.}

^{4) 50 • 15 = 750 (л) – літрів води викачав ІІ насос.}

^{5) 500 + 750 = 1250 (л) – літрів води викачали два насоси.}

Відповідь: два насоси викачали 1250 літрів води.

Завдання 4

Записали всі трикутники зі стороною АМ.

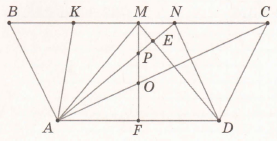
BAM, KAM, AMD, AMF, AMP, AMO, AMN, AMC, АМЕ

Завдання 5

Замість однакових букв поставили однакові цифри, замість різних букв – різні цифри.

АР • АР = РІКА    64 • 64 = 4096     МУХА + ДБАЄ = ДОБРЕ   8965 + 1377 = 10342

 

Сторінка 95

Завдання 5 Складена задача на ділення на вміщення

З одного поля зібрали 240 ц картоплі, а з другого — в 2 рази більше. 2/3 всієї картоплі розклали в мішки по 40 кг і завантажили їх на дві машини порівну. Скільки мішків поклали на кожну ма­шину?

Короткий запис №1 І поле — 240 ц ІІ поле — ?, у 2 рази більше	Короткий запис №2 І поле — 240 ц ІІ поле — 480 ц Всього — ?	Короткий запис №3 Розклали — ?, 2/3 від 720 ц
Короткий запис №4 480 ц = 4800 кг — це ? мішків по 40 кг	Короткий запис №5 1200 мішків — це 2 машини по ? мішків

Розв'язання

1) 240 • 2 = 480 (ц) – кілограмів картоплі зібрали з ІІ поля.

2) 240 + 480 = 480 + 20 + 220 = 720 (ц) – всього картоплі зібрали.

3) 720 : 3 • 2 = 480 (ц) = 48000 (кг) – кілограмів картоплі розклали в мішки.

4) 48000 : 40 = 4800 : 4 = 1200 (м.) – вийшло мішків.

5) 1200 : 2 = 600 (м.) – мішків поклали на кожну машину.

Відповідь: на кожну машину поклали 600 мішків.

Завдання 7 

Заповнили квадрати цифрами від 1 до 6 так, щоб у кожному рядку та кожному стовпці квадрата не було двох однакових цифр, також однакових цифр не повинно бути і у виділених прямо­кутниках.

4	3	2	6	1	5		5	6	4	2	1	3
5	6	1	2	3	4		1	2	3	6	4	5
3	4	6	1	5	2		4	3	5	1	6	2
2	1	5	3	4	6		6	1	2	3	5	4
1	2	4	5	6	3		2	4	6	5	3	1
6	5	3	4	2	1		3	5	1	4	2	6

Інші завдання дивись тут...