Відповіді 1 частина Лишенко математика 4 клас Завдання 268 – 289 ГДЗ до підручника нова програма 2021 року

Завдання 268 Дроби

Дві сьомих — 2/7, чотири шостих — 4/6, три восьмих — 3/8, три п'ятих — 3/5

Дріб	2/7	4/6	3/8	3/5
На частин поділено	7	6	8	5
Частин зафарбовано або взято	2	4	3	3

Завдання 269

П'ять сьомих — 5/7, чотири шостих — 4/6, сім восьмих — 7/8, дві дев'ятих — 2/9, шість дев'ятих — 6/9, одна десята — 1/10

Завдання 270 Довжина відрізка AB дорівнює 10 см. Чому дорівнюй 3/5 цього відрізка?

Розв'язання

1) Скільки сантиметрів в 1/5 відрізка AB?

10 : 5 = 2 (см)

2) Чому дорівнюй — відрізка AB?

2 • 3 = 6 (см)

Відповідь: довжина — відрізка AB дорівнює 6 см.

Завдання 272

4/7 від 28 = 28 : 7 • 4 = 4 • 4 = 16

3/5 від 360 = 360 : 5 • 3 = 72 • 3 = 216

_360 | 5

35 72

_10

х 72

216

3/7 від 364 = 364 : 7 • 3 = 52 • 3 = 156

_364 | 7

35 52

_14

х 52

156

4/9 від 738 = 738 : 9 • 4 = 82 • 4 = 328

_738 | 9

72 82

_18

х 82

328

Завдання 273 До складу сніжинок, що надають з неба, входять кристалики льоду та пилинки. Сніжинки, утворені лише з кристаликів льоду, становлять 1/4 загальної маси сніжинок, що впали на землю. Скільки сніжинок із 1000 сніжинок мають у своєму складі пилинки?

Короткий запис

Усього — 1000 сн.

З кристаликів льоду — ?, 1/4 від усього

З пилинками — ?, решта

Розв'язання

1-й спосіб

1) 1000 : 4 • 1 = 250 (сн.) – утворені лише кристаликами льоду;

2) 1000 – 250 = 750 (сн.) – решта або мають пилинки.

2-й спосіб

1) 1000 : 4 = 250 (сн.) – припадає на 1 частину;

2) 4 – 1 = 3 (ч.) – припадає на сніжинки з пилинками;

3) 250 • 3 = 750 (сн.) – мають пилинки;

Відповідь: 750 сніжинок мають у своєму складі пилинки.

Завдання 274 Сніг поглинає п'яту частину сонячних променів. Вологий чорнозем відбиває 1/20 сонячних променів, а решту — поглинає. На скільки променів більше відбив би сніг, ніж вологий чорнозем, якби на однакову площу кожного впало по 1000 променів?

Короткий запис

Усього — 1000 пр.

Поглинув би сніг — ?, 1/5 від усього

Відбив би сніг — ?, решта

Відбив би чорнозем — ?, 1/20 від усього

На скільки — ?

Розв'язання

1) 1000 : 5 • 1= 200 (пр.) – поглинає сніг;

2) 1000 – 200 = 800 (пр.) – решта або відбив би сніг;

3) 1000 : 20 • 1 = 50 (пр.) – відбив би вологий чорнозем.

4) 800 – 50 = 750 (пр.)

Відповідь: на 750 сонячних променів більше відбив би сніг, ніж вологий чорнозем.

Завдання 275 Побудуй два прямих кути зі спільною вершиною так, щоб утворилися 3 гострих кути й один тупий кут.

Завдання 276 Перший множник збільшили у 2 рази, а другий — зменшили на 10. Добуток не змінився. Знайди другий множник.

Розв'язання

1-й спосіб

Якщо перший множник збільшити у 2 рази, тоді добуток збільшиться у 2 рази. Але добуток також збільшиться у 2 рази, якщо другий множник збільшити у 2 рази.

Нехай х – другий множник, складемо рівняння змін з другим множником:

2(х – 10) = х

2х – 20 = х

2х – х = 20

х = 20

2-й спосіб

Нехай перший множник дорівнює а, а другий множник — b, тоді їхній добуток дорівнює a•b.

Збільшений удвічі перший множник дорівнює 2а, а зменшений на 10 другий множник — (b – 10).

Добуток не змінився, тому

а • b = 2а • (b – 10)

Поділимо ліву і праву частину рівності на змінну а:

b = 2 • (b – 10)

b = 2b – 20

2b – b = 20

b = 20

Відповідь: другий множник дорівнює 20

Завдання 277 Днів у кожному місяці

У листопаді 1/10 кількості днів ішов дощ. 2/3 днів місяця було похмуро, але без дощу. Решту часу було сонячно. Скільки днів світило сонце?

Короткий запис

Усього — 30 дн.

Дощило — ?, 1/10 від усього

Похмуро — ?, 2/3 від усього

Не було сонячно — ?, разом

Сонячно — ?, решта

Розв'язання

1) 30 : 10 • 1 = 3 (дн.) – йшов дощ;

2) 30 : 3 • 2 = 20 (дн.) – було похмуро;

3) 3 + 20 = 23 (дн.) – не було сонячно.

4) 30 – 23 = 7 (дн.)

Відповідь: сонце світило 7 днів у листопаді.

Завдання 278

12 • 18 : 36 = 3

16 • 42 : 28 = 24

32 • 26 : 16 = 52

х 12

108

_108 | 36

108 3

х 16

672

_672 | 28

56 24

_112

112

х 32

192

832

_832 | 16

80 52

_32

Завдання 279

2/3 від 1 хв = 1 хв : 3 • 2 = 60 с : 3 • 2 = 20 с • 2 = 40 с

1/2 від 1 хв = 1 хв : 2 • 1 = 60 с : 2 • 1 = 30 с • 1 = 30 с

3/4 від 1 хв = 1 хв : 4 • 3 = 60 с : 4 • 3 = 15 с • 3 = 45 с

2/5 від 1 хв = 1 хв : 5 • 2 = 60 с : 5 • 2 = 12 с • 2 = 24 с

3/10 від 1 хв = 1 хв : 10 • 3 = 60 с : 10 • 3 = 6 с • 3 = 18 с

Завдання 280 Накресли круг радіусом 2 см. Поділи його на 4 частини. Зафарбуй дві такі частини (зеленим кольором). Зафарбуй решту частин іншим кольором (білим).

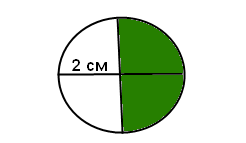
На скільки частин поділено круг? На 4 частини.

Скільки таких частин зафарбовано? Чотири.

4/4 = 1 Дріб у якого чисельник і знаменник рівні між собою, дорівнює одиниці.

Завдання 281

1) 1/2 = 3/6 1/2 < 4/6 3/4 < 6/6 2/4 < 2/3

2) 4/4 = 1 2/2 = 1 6/6 = 1 1 = 5/5

Завдання 282 Накресли відрізок AB = 10 см, а потім — ще два відрізки: відрізок MK завдовжки 2/5 відрізка AB і відрізок OE завдовжки 3/4 відрізка AB. Користуючись накресленими відрізками, порівняй дроби 2/5 і 3/4.

10 см = 100 мм

10 см : 5 • 2 = 2 см • 2 = 4 см – довжина відрізка МК.

100 мм : 4 • 3 = 25 мм • 3 = 75 мм = 7 см 5 мм – довжина відрізка ОЕ.

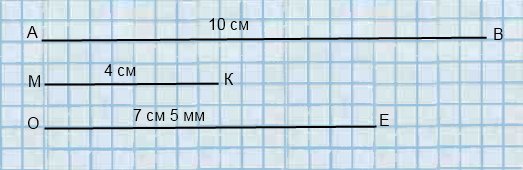
2/5 < 3/4

Завдання 283 У фермерському господарстві було 820 штук домашньої птиці. Гуси становили 1/5 всієї кількості. Кури – 3/4 від усіх птахів, а решта — качки. Скільки в господарстві було качок?

Короткий запис

Усього — 820 шт.

Гуси — ?, 1/5 від усього

Кури — ?, 3/4 від усього

Качки — ?, решта

Розв'язання

1) 820 : 5 • 1 = 164 (шт.) – було гусей;

2) 820 : 4 • 3 = 615 (шт.) – було курей;

3) 164 + 615 = 779 (шт.) – було гусей і курей разом.

4) 820 – 779 = 41 (шт.)

Відповідь: в господарстві було 41 качка.

� Досліди, як зміниться відповідь, якщо замінити 3/4 на 1/2

Короткий запис

Усього — 820 шт.

Гуси — ?, 1/5 від усього

Кури — ?, 1/2 від усього

Качки — ?, решта

Розв'язання

1) 820 : 5 • 1 = 164 (шт.) – було гусей;

2) 820 : 2 • 1 = 410 (шт.) – було курей;

3) 164 + 410 = 574 (шт.) – було гусей і курей разом.

4) 820 – 574 = 246 (шт.)

Відповідь: в господарстві було 246 качок.

Завдання 284 Оптова ціна перепелиних яєць, призначених для інкубатора, — 3 грн за одне яйце. А ціна яйця для споживання становить 2/5 ціни яйця для інкубатора. На скільки яйце для інкубатора дорожче, ніж яйце для споживання?

Короткий запис

Ціна інкубатор — 3 грн.

Ціна споживання — ?, 2/5 ціни інкубатора

На скільки — ?

Розв'язання

3 грн = 300 коп.

1) 300 : 5 • 2 = 60 • 2 = 120 (коп.) – ціна яйця для споживання.

2) 300 – 120 = 180 (коп.) = 1 грн 80 к.

Відповідь: на 1 грн 80 коп. дорожче яйце для інкубатора, ніж для споживання.

Завдання 285 За 3 десятки столових яєць господиня заплатила таку саму суму, як і за 2 десятки дієтичних. Ціна одного десятка столових яєць — 22 грн. Яка ціна десятка дієтичних яєць?

Вид яєць

За 1 десяток

Кількість

Вартість

Столові

22 грн

3 десятки

однакова

Дієтичні

2 десятки

Розв'язання

1) 22 • 3 = 66 (грн) – вартість 3 десятків столових яєць, або 2 десятків дієтичних яєць;

2) 66 : 2 = 33 (грн) – ціна 1 десятків дієтичних яєць.

Відповідь: ціна десятка дієтичних яєць 33 гривні.

Завдання 286 Сума двох чисел дорівнює 536. А їх різниця — 164. Знайди ці числа.

Нехай перше число дорівнює х, а друге — у, тоді за умовою задачі:

х + у = 536

х – у = 164

Виразимо невідому змінну х через у з першого рівняння:

х = 536 – у

і підставимо в друге рівняння:

536 – у – у = 164

536 – 2у = 164

2у = 536 – 164

2у = 372

у = 372 : 2

у = 186

х = 536 – у = 536 – 186 = 350

Відповідь: перше число 350, а друге число 186.

Завдання 287 Рівняння

(520 + 440) : х = 24

960 : х = 24

х = 960 : 24

х = 40

18 • х + 184 = 400

18 • х = 400 – 184

18 • х = 216

х = 216 : 18

х = 12

Завдання 288 Купили однакову кількість молодняку каченят і перепеленят. Ціна одного каченяти 30 грн, а одного перепеленяти — 1/3 ціни каченяти. За каченят заплатили 900 грн. Знайди вартість перепеленят.

Ціна

Кількість

Вартість

Каченята

30 грн

Однакова

900 грн

Перепеленята

?, 1/3 від ціни каченята

Розв'язання

1) 900 : 30 = 30 (шт.) – кількість каченят, або перепеленят;

1) 30 : 3 • 1 = 10 (грн) – ціна перепеленяти.