ГДЗ Математика 4 клас Будна Н О, Беденко М В завдання 72 - 104 частина 2 Відповіді Нова програма

Інші завдання дивись тут ...

Завдання 72 Рівняння

х + 12 = 24

х = 24 – 12

х = 12

х • 6 = 36

х = 36 : 6

х = 6

х – 25 = 25

х = 25 + 25

х = 50

х : 10 = 100

х = 100 • 10

х = 1000

х + 18 = 40

х = 40 – 18

х = 22

125 : х = 5

х = 125 : 5

х = 25

Завдання 73

1) 2 мм • 10 = 20 мм = 2 см

2 мм • 100 = 200 мм = 2 дм

2 мм • 1000 = 2000 мм = 2 м

2) 3 кг • 100 = 300 кг = 3 ц

5 г • 1000 = 5000 г = 5 кг

5 г • 1000000 = 5000000 г = 5 т

Завдання 74

2 мм • 1000 = 2000 мм = 2 м

2 см • 100 = 100 см = 2 м

2 ц • 10 = 20 ц = 2 т

5 м • 1000 = 5000 м = 5 км

Завдання 75 Письмове множення

х 56000

392000

х 15000

135000

х 3600

18000

х 2800

16800

Завдання 76

П’ятицифрове число помножили на одноцифрове. Скільки цифр могли отримати в добутку? Шість або п'ять цифр (наприклад, 10000 • 1 = 10000 і 99999 • 2 = 199998).

Завдання 77

Автобус 350 км подолав за 5 год, а потім ще їхав 8 годин. Яку відстань автобус проїхав потім, якщо швидкість була однакова?

Розв’язання

1) 350 : 5 = 70 (км/год) – швидкість

2) 70 • 8 = 560 (км)

Відповідь: потім автобус проїхав 560 кілометрів.

Завдання 78 Першого дня в магазині продали 342 м шовку, а протягом п’яти наступних днів — по b м шовку щодня. Скільки всього метрів шовку продали в магазині за ці дні? Розв’яжи задачу, склавши вираз.

Розв’язання

1) b • 5 (м) – продали протягом п'яти наступних днів;

2) 342 + b • 5 (м) – продали тканини в магазині.

Відповідь: 342 + b • 5 метрів.

Завдання 79 Письмове множення

х 101

505

х 16835

50505

х 22727

45454

х 12961

77766

х 11333

56665

х 33367

100101

Завдання 80

Поплавець у вигляді конуса гойдається на хвилях. Яку з цих фігур може окреслити на ньому вода? Фігуру №2.

Завдання 81

Моркву масою 360 кг розклали в 9 ящиків, а огірки — в 15 ящиків. Скільки кілограмів огірків розклали, якщо маса одного ящика однакова?

Розв’язання

1) 360 : 9 = 40 (кг) – маса одного ящика.

2) 40 • 15 = 600 (кг)

Відповідь: розклали 600 кілогрмів огірків.

Завдання 82 Письмове множення

х 35487

212922

х 37984

151936

х 45268

271608

х 48468

96936

Завдання 83

600 : 30 = 20

600 : 3 = 200

600 : 300 = 2

280 : 10 = 28

280 : 28 = 10

280 : 1 = 280

Завдання 84

х 86000

344000

х 120000

480000

х 29000

58000

Завдання 85, 86

Полічи і запиши, скільки квадратних сантиметрів у кожній фігурі. 6 см², 7 см², 4 см²

Завдання 87, 88

а) Якщо скласти фігуру із двох інших фігур, то площа утвореної фігури дорівнюватиме сумі площ цих двох фігур. Істинне

б) Якщо розрізати фігуру на декілька частин, то площа початкової фігури дорівнюватиме сумі площ отриманих частин. Істинне

в) Якщо від фігури відрізати якусь частину, то площа залишку дорівнюватиме різниці площ початкової фігури та відрізаної частини. Істинне.

Завдання 89 Порядок дій

(50 + 25) : (50 – 25) • 5 = 75 : 25 • 5 = 3 • 5 = 15

(15 + 5) • (15 – 5) : 100 = 20 • 10 : 100 = 200 : 100 = 2

Завдання 90

Перший токар виготовляє 40 деталей за 8 годин, а другий — стільки ж деталей за 10 годин. За скільки годин виготовлять 36 деталей обидва токарі разом, якщо продуктивність праці кожного з них не зміниться?

Розв'язання

1) 40 : 8 = 5 (д.) – виготовляє перший токар за 1 год;

2) 40 : 10 = 4 (д.) – виготовляє другий токар за 1 год;

3) 5 + 4 = 9 (д.) – виготовляють два токари разом за 1 год.

4) 36 : 9 = 4 (дн.)

Відповідь: за 4 дні.

Завдання 91

Склади і розв’яжи рівняння за малюнком.

х + х + х – 30 = 3

3 • х – 30 = 3

3 • х = 3 + 30

3 • х = 33

х = 33 : 3

х = 11

Завдання 92

¹⁰¹⁰⁰

¹⁰¹⁹⁹

¹⁰²⁹⁸

¹⁰³⁹⁷

¹⁰⁴⁹⁶

¹⁰⁵⁹⁵

¹⁰⁶⁹⁴

¹⁰⁷⁹³

¹⁰⁰⁰⁰

¹⁰⁰⁹⁹

¹⁰¹⁹⁸

¹⁰²⁸⁷

¹⁰³⁹⁶

¹⁰⁴⁹⁵

¹⁰⁵⁹⁴

¹⁰⁶⁹³

Завдання 93

х 48000

192000

х 160000

800000

х 101000

202000

Завдання 94

На будівництво підвозили цеглу автомобілем і трактором із причепом. Автомобіль за один рейс привозив 863 цеглини, а трактор — 2830 цеглин. Скільки цеглин привезли на будівництво протягом дня, якщо автомобіль зробив 7 рейсів, а трактор — 2 рейси?

Розв'язання

1) х 2830

19810 (ц.) – перевезли автомобілем за 7 рейсів;

2) х 2830

5660 (ц.) – перевезли трактором за 2 рейси.

3) + 19810

5660

25470 (ц.)

Відповідь: на будівництво привезли 25470 цеглин.

Завдання 95

1/4 від 2 год — це 2 год : 4 = 120 хв : 4 = 30 хв

1/8 від 4 год — це 4 год : 8 = 240 хв : 8 = 30 хв

1/9 від 3 год — це 3 год : 9 = 180 хв : 9 = 20 хв

1/6 від 3 год — це 3 год : 6 = 180 хв : 6 = 30 хв

1/5 від 1 год — це 1 год : 5 = 60 хв : 5 = 12 хв

Завдання 96

2 • 5 = 5 • 2 = 10 (см²)

2 • 4 = 4 • 2 = 8 (см²)

Завдання 97

Накресли прямокутник зі сторонами 2 см і 6 см та знайди його площу.

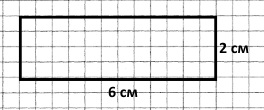
2 • 6 = 6 • 2 = 12 (см²).

Завдання 98 Порядок дій

24682 • 2 – 1212 • 2 = 46940 (42638 – 31527) • 6 – 6000 = 60666
х 24682 2 49364	х 1212 2 2424	_ 49364 2424 46940	_ 42638 31527 11111	х 11111 6 66666	_ 66666 6000 60666

Завдання 99

Один маляр може пофарбувати 300 рам за 10 днів, а другий — за 15 днів. За скільки днів можуть пофарбувати 150 рам обидва малярі разом, якщо продуктивність праці кожного з них не зміниться?

Розв'язання

1) 300 : 10 = 30 (р.) – фарбує один маляр за 1 день;

2) 300 : 15 = 20 (р.) – фарбує другий маляр за 1 день;

3) 30 + 20 = 50 (р.) – фарбують обидва маляри разом за 1 день.

4) 150 : 50 = 3 (дн.)

Відповідь: за 3 дні.

Завдання 100 Рівняння

3 + х = 8

х = 8 – 3

х = 5

5 + х = 10

х = 10 – 5

х = 5

3 + х + 5 + х = 8 + 10

8 + 2х = 18

2х = 18 – 8

2х = 10

х = 10 : 2

х = 5

Завдання 101

Склади і розв’яжи задачу за даними таблиці.

Ковзанярка проїхала 28 км зі швидкістю 14 км/год, а лижниця деяку відстань зі швидкістю 11 км/год. Яку відстань проїхала лижниця, якщо час руху однаковий?

Розв’язання

1) 28 : 14 = 2 (год) – час руху

2) 11 • 2 = 22 (км)

Відповідь: лижниця проїхала 22 кілометри.

Завдання 102

Часовий проміжок тривалістю 5 хвилин зобразили на прямій у вигляді відрізка ОМ. Інші часові проміжки позначили літерами А, В, С, D, Е.

Часовому проміжку тривалістю 250 с відповідає літера В

Часовому проміжку тривалістю 400 с відповідає літера D

Завдання 103 Порядок дій

Знайди значення тільки тих виразів, у яких першою буде дія множення.

5 • 20 • 10 = 100

100 : (5 • 2) = 10

64 – 32 • 2 = 0

(64 – 32) • 2

16 • 2 • 3 – 16 = 96 – 16 = 80

900 : (40 : 2) • 6

Завдання 104

Щоб покрити дах великого будинку черепицею, потрібно 3540 плиток, а для даху малого будинку достатньо 784 плитки. Скільки плиток черепиці потрібно, щоби покрити дахи 8 великих і 3 малих будинків?

Розв'язання