ГДЗ 4 клас Заїка математика завдання 150 – 169 Частина 2 Нова програма 2021 року Відповіді до підручника Ответы к учебнику

Інші завдання дивись тут...

Завдання 150

Периметр квадрата 24 см. Яка площа цього квадрата? Виконай обчислення за планом.

Р = 24 см

S _кв. – ?

Розв'язання

1) 24 : 4 = 6 (см) – довжина сторони квадрата.

2) 6 • 6 = 36 (см²) – площа цього квадрата.

Відповідь: 36 см².

Завдання 151

Побудуй у зошиті квадрати зі сторонами 1 см та 1 дм. Розбий великий квадрат на квадратні сантиметри (як на рис.).

1) 1 дм² = 100 см²

2) Яку частину становить 1 см² від 1 дм²? 1 см² = 1/100 дм²

3) 1/4 дм² = 100 см² : 4 = 25 см²

1/2 дм² = 100 см² : 2 = 50 см²

Завдання 152

Скільки одиничних квадратів зі стороною 1 мм поміститься в одиничному квадраті зі стороною 1 см? 100

1 см ² = 100 мм²

Завдання 153, 154

1 м = 10 дм, тому 1 м² = 10 • 10 (дм²) = 100 дм², 1 дм² = 1/100 м²

1 м = 100 см, тому 1 м² = 100 • 100 (см²) = 10000 см², 1 см² = 1/10000 м²

Завдання 155

Довжина серветки 23 см, ширина — 10 см. Визнач площу серветки у квадратних сантиметрах; квадратних міліметрах.

S = 23 см • 10 см = 230 см²

S = 230 мм • 100 мм = 23000 мм²

Завдання 156

Мама може прополоти 24 рядки цибулі за 3 год, а її донька — за 6 год. За скільки годин мама і донька зможуть прополоти 24 рядки, працюючи разом?

Розв'язання

1) 24 : 3 = 8 (р.) – прополе за 1 год мама

2) 24 : 6 = 4 (р.) – прополе за 1 год донька

3) 8 + 4 = 12 (р.) – прополють за 1 год мама і донька разом

4) 24 : 12 = 2 (год)

Відповідь: зможуть прополоти разом за 2 години, працюючи разом.

Будьте маминими помічниками!

Завдання 157

Один маляр може пофарбувати паркан, площа якого становить 240 м², за 12 год. Інший маляр цей самий паркан може пофарбувати за 24 год. За скільки годин обидва маляри пофарбують цей паркан, працюючи разом?

Розв'язання

1) 240 : 12 = 20 (м²) – фарбує за 1 год перший маляр.

2) 240 : 24 = 10 (м²) – фарбує за 1 год другий маляр.

3) 20 + 10 = 30 (м²) – фарбують за 1 год разом.

4) 240 : 30 = 8 (год)

Відповідь: за 8 годин обидва маляри пофарбують цей паркан, працюючи разом.

Завдання 158

(729 : 1 – 729 • 0) • 3 = 729 • 3 = 2187

(154320 + 45680) : 1000 = 200000 : 1000 = 200

х 729

2187

+ 154320

45680

200000

Завдання 159

а) Площа підлоги класної кімнати 54 м², ширина — 6 м. Обчисли довжину класної кімнати.

Розв'язання

54 : 6 = 9 (м)

Відповідь: довжина класної кімнати 9 м.

б) Площа підлоги класної кімнати 54 м², а площа вікон у класі становить 1/6 площі підлоги. Чому дорівнює площа вікон класної кімнати?

Розв'язання

54 : 6 • 1 = 9 (м²)

Відповідь: площа вікон класної кімнати 9 м².

Завдання 160

Побудуй прямокутник завдовжки 8 см і завширшки 3 см 5 мм. Обчисли його периметр і площу.

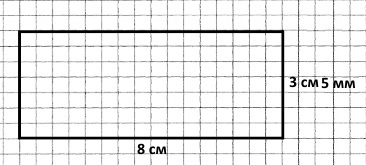
Розв'язання

8 см = 80 мм, 3 см 5 мм = 35 мм

Р = (8 см + 3 см 5 мм) • 2 = 11 см 5 мм • 2 = 23 см – периметр прямокутника.

S = 80 мм • 35 мм = 2800 мм² = 28 см² – площа прямокутника.

Завдання 161, 162

Площі ділянок землі, здебільшого, вимірюють сотками (арами) та гектарами.

1 сотка (або 1 ар) — дорівнює площі квадрата зі стороною 10 м.

1 а = 10 м • 10 м = 100 м²

Один гектар дорівнює площі квадрата зі стороною 100 м.

1 га = 100 м • 100 м = 10000 м²

Завдання 163

Ділянка має форму прямокутника завдовжки 100 м і завширшки 50 м. Чому дорівнює площа ділянки? Скільки соток має ця ділянка?

Розв'язання

S = 100 м • 50 м = 5000 м² = 50 • 100 м² = 50 а

Відповідь: площа ділянки 50 а, або 50 соток.

Завдання 164

а) 1 а = 100 м² 2 а = 200 м²	4 а = 400 м² 6 а = 600 м²	10 а = 1000 м² 100 а = 10000 м²
б) 400 м² = 4 а 500 м² = 5 а	1000 м² = 10 а 3000 м² = 30 а	6000 м² = 60 а 10000 м² = 100 а

Завдання 165

Розшифруй назву міста козацької слави.

А 3150 – 150 : 3 – 3000 = 3150 – 50 – 3000 = 100

Я 59084 – 8739 • 1 = 59084 – 8739 = 50345

О 1414 • 1 – 4141 • 0 = 1414

І 3042 • 0 + 1 • 17300 = 17300

Ж 3042 • (0 + 1) + 17300 = 3042 + 17300 = 20342

Р 117 • 7 + 7 • 107 = 7 • (117 + 107) = 7 • 224 = 1568

П 342 • 5 – 355 • 2 = 1710 – 710 = 1000

Ж 16245 + 132 • 8 = 16245 + 1056 = 17301

З 480 : 15 – 736 : 23 = 32 – 32 = 0

З	А	П	О	Р	І	Ж	Ж	Я
0	100	1000	1414	1568	17300	17301	17301	50345

Завдання 166

Фермерське господарство вирощує кукурудзу, соняшник, пшеницю і буряк на площі 320 га. Відомо, що соняшник і пшениця займають однакову площу, а площа, засіяна кукурудзою, становить 1/2 площі, відведеної під пшеницю, площа під буряком у 3 рази більша від площі під кукурудзою. Яку площу займає кожна культура? Скористайся планом ділянки та розв’яжи задачу.

^{Короткий запис}

^{Соняшник або пшениця — ?, однакова площа}

^{Кукурудза — ?, 1/2 від площі пшениці}

^{Буряк — ?, у 3 рази більше від площі кукурудзи.}

^{Загальна площа — 320 га}

Розв'язання

1-й спосіб

1) 1 + 2 + 2 + 3 = 8 (ч.) – всього частин

2) 320 : 8 = 40 (га) – площа під кукурудзою

3) 40 • 2 = 80 (га) – площа поля під соняшником або пшеницею

4) 40 • 3 = 120 (га) – площа поля під буряком

2-й спосіб

Нехай х (га) — площа під кукурудзою, тоді 2х (га) — площа під соняшником, 2х (га) — площа під пшеницею, 3х (га) — площа під буряком. Складемо рівняння:

х + 2х + 2х + 3х = 320

8х = 320

х = 320 : 8

х = 40 (га) – площа під кукурудзою.

40 • 2 = 80 (га) – площа під соняшником або пшеницею.

40 • 3 = 120 (га) – площа під буряком.

Відповідь: площа під кукурудзою 40 га, площа під соняшником або пшеницею 80 га, площа під буряком 120 га.

Завдання 167

На ділянці прямокутної форми завдовжки 30 м і завширшки 20 м виростили картоплю. З кожного ара зібрали в середньому по 200 кг картоплі. Скільки центнерів картоплі зібрали з цієї ділянки?

Розв'язання

1) 30 • 20 = 600 (м²) = 6 (а) – площа ділянки

2) 200 • 6 = 1200 (кг) = 12 (ц)

Відповідь: з цієї ділянки зібрали 12 центнерів.

Завдання 168

Добери кілька розв'язків кожної нерівності:

400 • х < 1600, при х = 0, 1, 2, 3	8000 : х > 200, при х = 1, 2, 3, 10
600 – х < 360, при х = 250, 251, 252	15000 + х < 15015, при х = 0, 1, 2, 3