ГДЗ Істер 5 клас математика завдання 823 - 846 § 23 Прямокутник Квадрат ВІДПОВІДІ до підручника

Інші завдання дивись тут...

Завдання 823

Виміряй сторони прямокутника та за формулою обчисли його периметр.

^{Короткий запис}

^{а = 12 мм, b = 18 мм, P — ?}

Розв'язання

Р = (а + b) • 2 = (12 + 18) • 2 = 30 • 2 = 60 (мм) = 6 (см)

Відповідь: 6 см.

Завдання 824

Знайди периметр квадрата, якщо довжина його сторони дорівнює 5 см; 27 мм; 3 м.

Короткий запис

а = 5 см, а = 27 мм, а = 3 м, P — ?

Розв'язання

Формула: Р = 4а

1) 5 • 4 = 20 (см) – периметр квадрата зі стороною 5 см;

2) 27 • 4 = 108 (мм) – периметр квадрата зі стороною 27 мм;

3) 3 • 4 = 12 (м) – периметр квадрата зі стороною 3 м.

Завдання 825

Накресли квадрат, сторона якого дорівнює 25 мм. Знайди периметр цього квадрата.

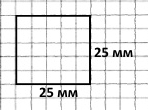
Розв'язання

Р = 25 • 4 = 100 (мм) = 10 (см) – периметр квадрата.

Відповідь: 10 см.

Завдання 826

За допомогою лінійки накресли прямокутник зі сторонами 4 см і 3 см. Знайди його периметр.

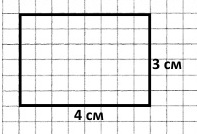
Р = (4 + 3) • 2 = 7 • 2 = 14 (см) – периметр прямокутника.

Відповідь: 14 см.

Завдання 827

Одна зі сторін прямокутника завдовжки 16 см, а інша — на 8 см довша. Знайди периметр прямокутника.

^{Короткий запис}

^{а = 16 см}

b — ?, на 8 см більше

^P — ?

Розв'язання

1) 16 + 8 = 24 (см) – довжина іншої сторони;

2) Р = (16 + 24) • 2 = 40 • 2 = 80 (см) – периметр прямокутника.

Відповідь: 80 см.

Завдання 828

Одна зі сторін земельної ділянки прямокутної форми, зображеної на малюнку, прилягає до паркану сусідньої ділянки. Знайди довжину огорожі, якою треба огородити цю ділянку.

Розв'язання

1 спосіб

1) (45 + 20) • 2 = 130 (м) – довжина всіх сторін цієї ділянки;

2) 130 – 45 = 85 (м) – довжина огорожі ділянки.

2 спосіб

1) 20 • 2 = 40 (м) – довжина двох сторін цієї ділянки;

2) 40 + 45 = 85 (м) – довжина огорожі ділянки.

Відповідь: 85 м.

Завдання 829

а	12 см	4 дм	5 м	18 см	7 дм	60 м
b	8 см	16 дм	1 м	5 см	3 дм	40 м
P	40 см	40 дм	12 м	46 см	20 дм	200 м
	(12 + 8) • 2 = 20 • 2 = 40 40 : 2 – 4 = 20 – 4 = 16		12 : 2 – 1 = 6 – 1 = 5 46 : 2 – 18 = 23 – 18 = 5		(7 + 3) • 2 = 10 • 2 = 20 200 : 2 – 40 = 100 – 40 = 60

Завдання 830 Одиниці вимірювання

Порівняй периметр прямокутника зі сторонами 12 см і 9 см з периметром квадрата зі стороною 1 дм.

Розв'язання

^{1 дм = 10 см}

1) (12 + 9) • 2 = 21 • 2 = 42 (см) – периметр прямокутника;

2) 10 • 4 = 40 (см) – периметр квадрата.

42 см > 40 см

Відповідь: периметр прямокутника більший, ніж периметр квадрата.

Завдання 831

Порівняй периметр квадрата зі стороною 5 см з периметром прямокутника зі сторонами 24 мм і 26 мм.

Розв'язання

1) (24 + 26) • 2 = 50 • 2 = 100 (мм) = 10 (см) – периметр прямокутника;

2) 5 • 4 = 20 (см) – периметр квадрата.

20 см > 10 см

Відповідь: периметр квадрата більший, ніж периметр прямокутника.

Завдання 832

Периметр земельної ділянки прямокутної форми дорівнює 400 м, а довжина однієї з його сторін — a м. Склади буквений вираз для обчислення довжини іншої сторони. Знайди значення виразу, якщо a = 80.

Розв'язання

1) 400 : 2 = 200 (м) – сума двох суміжних сторін прямокутника;

2) 200 – а (м) – довжина іншої сторони прямокутника.

Вираз: 400 : 2 – а = 200 – а

Якщо а = 80, тоді 200 – а = 200 – 80 = 120 (м)

Відповідь: 200 – a, 120 м.

Завдання 833

Периметр прямокутника дорівнює 100 м, а одна з його сторін дорівнює b м. Склади буквений вираз для обчислення другої сторони. Обчисли його значення, якщо b = 22 м.

Розв'язання

1) 100 : 2 = 50 (м) – сума двох суміжних сторін прямокутника;

2) 50 – b (м) – довжина іншої сторони прямокутника.

Вираз: 100 : 2 – b = 50 – b

Якщо b = 22, тоді 50 – b = 50 – 22 = 28 (м)

Відповідь: 50 – b, 28 м.

Завдання 834

Сторони прямокутника дорівнюють 8 дм і 14 дм. Обчисли сторону квадрата, периметр якого дорівнює периметру прямокутника.

Розв'язання

1) (8 + 14) • 2 = 44 (дм) – периметр прямокутника або периметр квадрата;

2) 44 : 4 = 11 (дм) – довжина сторони квадрата.

Відповідь: 11 дм.

Завдання 835

Периметр прямокутника, довжина якого дорівнює 10 см, дорівнює периметру квадрата зі стороною 7 см. Знайди ширину прямокутника.

Розв'язання

1 спосіб

1) 7 • 4 = 28 (см) – периметр квадрата або периметр прямокутника;

2) 28 : 2 = 14 (см) – півпериметр прямокутника або сума суміжних сторін;

3) 14 – 10 = 4 (см) – ширина прямокутника.

2 спосіб

1) 7 • 4 = 28 (см) – периметр квадрата або периметр прямокутника;

2) 10 + 10 = 20 (см) – дві довжини прямокутника;

3) 28 – 20 = 8 (см) – дві ширини прямокутника;

4) 8 : 2 = 4 (см) – ширина прямокутника.

Відповідь: 4 см.

Завдання 836

Із шматка дроту виготовили прямокутник зі сторонами 14 см і 6 см. Чи можна було із цього шматка дроту виготовити:

1) квадрат зі стороною 10 см;

Розв'язання

1) (14 + 6) • 2 = 20 • 2 = 40 (см) – периметр прямокутника;

2) 40 : 4 = 10 (см) – довжина сторони квадрата.

Відповідь: можна.

2) прямокутник зі сторонами 10 см і 11 см?

Розв'язання

1 спосіб

1) (14 + 6) • 2 = 20 • 2 = 40 (см) – периметр прямокутника зі сторонами 14 см і 6 см;

2) (10 + 11) • 2 = 42 (см) – периметр прямокутника зі сторонами 10 см і 11 см.

40 < 42

2 спосіб

1) (14 + 6) • 2 = 20 • 2 = 40 (см) – периметр прямокутника зі сторонами 14 см і 6 см;

2) 40 : 2 = 20 (см) – сума двох суміжних сторін прямокутника;

3) 10 + 11 = 21 (см) – сума двох суміжних сторін прямокутника зі сторонами 10 см і 11 см;

20 < 21

Відповідь: не можна.

Завдання 837

Від прямокутника ABCD відрізали квадрат AMND, периметр якого дорівнює 28 см. Знайди довжину відрізка MB, якщо периметр прямокутника ABCD дорівнює 40 см.

Розв'язання

1 спосіб

1) 28 : 4 = 7 (см) – довжина сторони квадрата AMND;

2) 40 : 2 = 20 (cм) – півпериметр ABCD або сума суміжних сторін AB i ВС;

3) 20 – 7 = 13 (см) – довжина сторони АВ;

4) 13 – 7 = 6 (см) – довжина відрізка МВ.

2 спосіб

Дивіться на малюнок в підручнику для кращого розуміння способу.

1) 40 – 28 = 12 (см) – сума довжин рівних сторін MB і NC;

2) 12 : 2 = 6 (см) – довжина сторони МВ.

Відповідь: 6 см.

Завдання 838

Периметр прямокутника дорівнює 42 см. Знайди його сторони, якщо:

1) одна з них на 3 см більша за іншу;

Розв'язання

1 спосіб

1) 42 : 2 = 21 (см) – сума довжини і ширини прямокутника;

2) 21 – 3 = 18 (см) – довжина і ширина порівно;

3) 18 : 2 = 9 (см) – ширина прямокутника;

4) 9 + 3 = 12 (см) – довжина прямокутника.

2 спосіб

Нехай одна сторона дорівнює х см, тоді друга сторона — (х+3) см, а периметр — 42 см. Складаємо рівняння:

(х + х + 3) • 2 = 42

2х + 2х + 6 = 42

4х + 6 = 42

4х = 42 – 6

4х = 36

х = 9 (см) – ширина прямокутника;

9 + 3 = 12 (см) – довжина прямокутника.

Відповідь: 9 см, 12 см.

Інший спосіб розв'язування рівняння

(х + х + 3) • 2 = 42

х + х + 3 = 42 : 2

2х + 3 = 21

2х = 21 – 3

2х = 18

х = 18 : 2

х = 9

2) одна з них удвічі більша за іншу.

Розв'язання

1 спосіб

1) 42 : 2 = 21 (см) – сума довжини і ширини прямокутника;

2) 1 + 2 = 3 (ч.) – частин припадає на 21 см;

3) 21 : 3 = 7 (см) – ширина прямокутника;

4) 7 • 2 = 14 (см) – довжина прямокутника.

2 спосіб

Нехай одна сторона дорівнює х см, тоді друга сторона — 2х см, а периметр — 42 см. Складаємо рівняння:

(х + 2х) • 2 = 42

3х • 2 = 42

6х = 42

х = 42 : 6

х = 7 (см) – ширина прямокутника;

2 • 7 = 14 (см) – довжина прямокутника.

Відповідь: 7 см, 14 см.

Інший спосіб розв'язування рівняння

(х + 2х) • 2 = 42

х + 2х = 42 : 2

3х = 21

х = 21 : 3

х = 7

Завдання 839

Одна зі сторін прямокутника на 2 дм більша за іншу. Знайди ці сторони, якщо периметр прямокутника дорівнює 40 дм.

Розв'язання

1 спосіб

1) 40 : 2 = 20 (дм) – сума довжини і ширини прямокутника;

2) 20 – 2 = 18 (дм) – довжина і ширина порівно;

3) 18 : 2 = 9 (дм) – ширина прямокутника;

4) 9 + 2 = 11 (см) – довжина прямокутника.

2 спосіб

Нехай одна сторона дорівнює х дм, тоді друга — (х + 2) дм, а периметр — 40 дм. Складаємо рівняння:

(х + х + 2) • 2 = 40

2х + 2х + 4 = 40

4х + 4 = 40

4х = 40 – 4

4х = 36

х = 36 : 4

х = 9 (дм) – ширина прямокутника;

9 + 2 = 11 (дм) – довжина прямокутника.

Відповідь: 9 дм, 11 дм.

Інший спосіб розв'язування рівняння

(х + х + 2) • 2 = 40

х + х + 2 = 40 : 2

2х + 2 = 20

2х = 20 – 2

2х = 18

х = 18 : 2

х = 9

Завдання 840

Периметри двох прямокутників рівні. Чи можна стверджувати, що сторони одного прямокутника дорівнюють сторонам іншого? Наведи приклади.

Розв'язання

Припустимо, що периметри двох прямокутників однакові і дорівнюють 10 см, тоді

10 : 2 = 5 (см) – сума ширини і довжини прямокутника.

Це можуть бути прямокутники зі сторонами 4 см і 1 см, 2 см і 3 см, отже, два прямокутники мають різні сторони.

Відповідь: не можна стверджувати.

Перевірка: (4 + 1) • 2 = 5 • 2 = 10 (см) і (2 + 3) • 2 = 5 • 2 = 10 (см)

Завдання 841

Знайди довжину сторони квадрата, якщо вона на 12 см менша від його периметра.

Розв'язання

1 спосіб

Нехай сторона квадрата дорівнює х см, тоді периметр квадрата — 4х см, а різниця периметрів (4х – х) дорівнює 12 см. Складаємо рівняння:

4х – х = 12

3х = 12

х = 12 : 3

х = 4

2 спосіб

Оскільки периметр квадрата є сумою 4 рівних сторін, то різниця периметра квадрата і його сторони:

1) 4 – 1 = 3 (ч.) – стільки частин довжини квадрата дорівнюють 12 см;

2) 12 : 3 = 4 (см) – довжина сторони квадрата.

Відповдіь: сторона квадрата 4 см.

Завдання 842 Знайди значення виразів

1) 15a – a = 14а

Якщо a = 97, тоді 14а = 14 • 97 = 1358

Якщо а = 28, тоді 14а = 14 • 28 = 392

2) 19n + 16n = 35n

Якщо n = 100, тоді 35n = 35 • 100 = 3 500

Якщо n = 15, тоді 35n = 35 • 15 = 525

х 14

126

1358

х 14

112

392

х 35

175

525

Завдання 843

Відстань між Херсоном і Луцьком становить 870 км. О 12 годині з Херсона до Луцька виїхав автобус зі швидкістю 85 км/год. О 14 годині з Луцька до Херсона виїхав автомобіль зі швидкістю 90 км/год. О котрій годині вони зустрінуться?

Розв'язання

1) 14 – 12 = 2 (год) – час руху автобуса до старту автомобіля;

2) 85 • 2 = 170 (км) – проїхав відстань автобус до старту автомобіля;

3) 870 – 170 = 700 (км) – відстань між ними, коли стартував автомобіль;

4) 85 + 90 = 175 (км/год) – швидкість зближення;

5) 700 : 175 = 4 (год) – через стільки часу зустрінуться або час руху автомобіля;

6) 14 год + 4 год = 18 год – о тій годині зустрінуться.

Відповідь: о 18 годині.

Завдання 844

Три кухарки за 4 год зліпили 252 вареники. За скільки годин дві кухарки зліплять 294 вареники, якщо працюватимуть з такою самою продуктивністю праці?

Короткий запис

3 к. — 4 год — 252 в.

2 к. — ? год — 294 в.

Розв'язання

1) 252 : 4 = 63 (в./год) – продуктивність трьох кухарок;

2) 63 : 3 = 21 (в./год) – продуктивність однієї кухарки;

3) 21 • 2 = 42 (в./год) – продуктивність двох кухарок;

4) 294 : 42 = 7 (год) – час, за який дві кухарки зліплять 294 вареники.

Відповідь: за 7 годин.

Завдання 845 Дії з іменованими величинами

Проєктна діяльність. Оля навчається у 5 класі. Вона прокидається о 7.00, а лягає спати о 21.00. Оптимальні інтервали між прийомами їжі для її віку — 3 год. Скільки разів протягом дня має харчуватися Оля? Сплануйте розклад прийомів їжі для Олі, якщо останній має бути не пізніше як за 1 год 30 хв до сну.

Розклад:

21 год – 1 год 30 хв = 20 год 60 хв – 1 год 30 хв = 19 год 30 хв – вечеря.

19 год 30 хв – 3 год = 16 год 30 хв – полуденок.

16 год 30 хв – 3 год = 13 год 30 хв – обід.

13 год 30 хв – 3 год = 10 год 30 хв – другий сніданок.

10 год 30 хв – 3 год = 7 год 30 хв – сніданок.

Відповідь: сніданок о 7 год 30 хв, другий сніданок о 10 год 30 хв,

обід о 13 год 30 хв, полуденок о 16 год 30 хв, вечеря о 19 год 30 хв.

Завдання 846

Знайди числові значення фігур.

Розв'язання

Позначимо квадрат через змінну х, трикутник через змінну у, а круг через змінну z.