Завдання 82
Фігури: відрізок (АВ), промінь (ОВ), пряма (MN), кут (AOB), ламана (ABCD)
Завдання 83
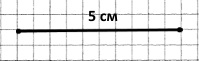
Накресліть відрізок, довжина якого дорівнює сумі довжин відрізків, зображених на рисунку 5.
3 + 2 = 5 (см) – довжина відрізка
Завдання 84
Накресліть відрізок АВ завдовжки 6 см 5 мм і відрізок CD, на 2 см 8 мм коротший від відрізка АВ.
Розв'язання
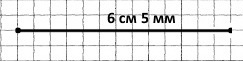
_6 см 5 мм
2 см 8 мм
3 см 7 мм – довжина відрізка CD
Завдання 85
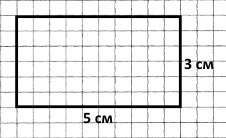
1) (5 + 3) • 2 = 16 (см) – периметр прямокутника
2) 5 • 3 = 15 (см) – площа прямокутника
Завдання 86
Перерисуйте в зошит трикутник, зображений на рисунку 6, і знайдіть його периметр.
5 + 4 + 3 = 12 (см) – периметр трикутника
Завдання 87
Довжина футбольного поля (рис. 7) дорівнює 105 м, а периметр — 320 м. Знайдіть ширину поля.
Розв'язання
1) 320 : 2 = 160 (м) – довжина і ширина поля
2) 160 – 105 = 55 (м)
Відповідь: ширина поля 55 метрів.
Завдання 88
Ширина ділянки прямокутної форми дорівнює 12 м, а площа — 180 м2. Знайдіть довжину ділянки.
Розв'язання
180 : 12 = 15 (м)
Відповідь: довжина ділянки 15 метрів.
Завдання 89
Для облаштування території новобудови на ділянці, розміри якої вказано на рисунку 8, планують засіяти траву. Скільки для цього потрібно кілограмів насіння, якщо на 1 м2 землі засівати 20 г насіння? Рис. 8
Розв'язання
1) 20 • 40 + (80 – 20) • 10 = 800 + 600 = 1400 (м2) – площа ділянки
2) 1400 • 20 = 28000 (г) = 28 (кг)
Відповідь: потрібно 28 кг насіння.
Завдання 90
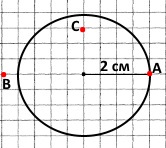
Побудуйте коло з центром у точці О, радіус якого дорівнює 2 см. Позначте точки А, В, С такі, що ОА = 20 мм, ОВ = 25 мм, ОС = 15 мм. Які з позначених точок лежать на колі? Точка А.
Завдання 91
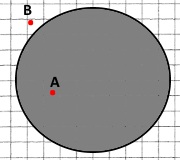
Побудуйте круг, діаметр якого дорівнює 48 мм. Позначте деяку точку А, яка належить кругу, і деяку точку В, яка йому не належить.
Завдання 92
Назвіть фігури, зображені на рисунку 9. Скільки вершин, ребер, граней має перша з цих фігур? Остання фігура?
Паралелепіпед (8 вершин, 12 ребер, 6 граней)
Куб
Чотирикутна піраміда
Трикутна піраміда (4 вершини, 6 ребер, 4 граней)
Завдання 93
Назвіть фігури, зображені на рисунку 10. Куля, циліндр, конус
Завдання 94 Ділення з остачею
У парку росте листяних дерев у 4 рази більше, ніж хвойних. Чи може загальна кількість цих дерев дорівнювати 482? Ні, не може. бо 482 не ділиться націло на 5.
х + 4 • х = 482
5 • х = 482
х = 482 : 5
х = 96 (ост. 2)
Завдання 95
Чи можна покласти 45 яблук у два пакети так, щоб в одному пакеті було на 2 яблука більше, ніж у другому? Ні, не можна, бо 43 не ділиться націло на 2.
х + х + 2 = 45
2 • х = 43
х = 43 : 2
х = 21 (ост. 1)
Завдання 96
За книжку й зошит Оксана заплатила 65 грн, а її подруга Надія за таку саму книжку і такі самі 4 зошити — 80 грн. Знайдіть ціну книжки.
Розв'язання
1) 80 – 65 = 15 (грн) – заплатила Надія за 3 зошити
2) 15 : 3 = 5 (грн) – ціна зошита
3) 65 – 5 = 60 (грн)
Відповідь: ціна книжки 60 гривень.
Завдання 97
Якби Гриць мав ще половину тих грошей, що він має, та ще 2 грн, то в нього було б 50 грн. Скільки грошей має хлопець?
Розв'язання
х : 2 + 2 = 50
х : 2 = 50 – 2
х : 2 = 48
х = 48 • 2
х = 96 (грн)
Хлопець має 96 гривні.
Завдання 98
Троє футболістів розташовані на футбольному полі так, що попарні відстані між ними є різними. Кожен футболіст має м’яч. У певний момент часу кожен футболіст пасує м’яч найближчому до себе футболісту. Доведіть, що після перетасовки:
1) знайдуться два футболісти, які пасували м’ячі один одному;
2) знайдеться футболіст без м’яча.
Завдання 99. Аркуш паперу розрізали на 10 частин, потім деякі з цих частин розрізали знову на 10 частин. Коли підрахували загальну кількість частин, то їх виявилося 48. Доведіть, що підрахунок був неправильним.
(10 – 4) + 10 • 4 = 46