Завдання 1497 Елементи комбінаторики

Скільки двоцифрових чисел можна записати за допомогою цифр 0, 3, 7 і 9, якщо в записі чисел цифри можуть повторюватися? 30, 33, 37, 39, 70, 73, 77, 79, 90, 93, 97, 99

Скільки всього є правильних дробів, знаменник кожного з яких дорівнює 18? Менший від 5?

Дріб х/18 — правильний, маємо дроби: 1/18, 2/18, 3/18, ..., 17/18, тобто 17 правильних дробів.

Завдання 1499 

Скількома різними способами можна розмістити двох кролів у три клітки?

Розв’язання

Позначимо два кролі: А, В

Позначимо три клітки: 1, 2, 3

Способи: А1, А2, А3,  В1, В2, В3, АВ1, АВ2, АВ3    

Відповідь: 9 способів.

Із 3 дівчат і 3 хлопців потрібно сформувати дует, до якого входила б одна дівчина й один хлопець. Скількома способами це можна зробити?

Розв’язання

Позначимо трьох дівчат: А, В, С

Позначимо трьох хлопців: 1, 2, 3

Способи: А1, А2, А3, В1, В2, В3, С1, С2, С3    

Відповідь: 9 способів.

Накресліть промінь з початком у точці А і позначте такі його точки B і C, щоб AB = 3 см, BC = 4 см.

Накресліть ламану ABCD, якщо AB = 4 см, ланка BC в 1,2 раза довша за AB і на 2 см довша за CD.

Розв'язання

1) 4 • 1,2  = 4,8 (см) – ланка ВС.

2) 4,8 – 2  = 2,8 (см) – ланка CD.

Треба накреслити ламану з таких ланок: АВ = 4 см, ВС = 4,8 см, СD = 2,8 см.

На рисунку 201 AB = 14 см, AM = 5 см. Знайдіть довжину відрізка МN, якщо AN = MB.

На рисунку 202 кут MON — розгорнутий, ∠LON = 35°. Знайдіть величину кута KOL, якщо:

2) ∠MOK = 72°.

За допомогою лінійки і транспортира побудуйте трикутник, дві сторони якого дорівнюють 3 см і 4 см, а кут між ними — 110°. Cамостійно.

Побудуйте прямокутник, довжина якого дорівнює 5 см, а площа — 12 см².

Розв'язання

12 : 5  = 2,4 (см) – ширина прямокутника.

Дві сторони трикутника дорівнюють по 8 см, а його периметр — 26 см. Знайдіть довжину третьої сторони трикутника.

Розв'язання

26 – (8 + 8) = 10 (см) – третя сторона.

Відповідь: 10 см.

Периметр прямокутника дорівнює 6,8 дм, а його довжина на 6 см більша за ширину. Знайдіть площу прямокутника.

Розв'язання

Нехай ширина прямокутника х см, тоді довжина (х + 6) см. Складаємо рівняння.

(х + х + 6) • 2 = 68

2х + 6 = 34

2х = 34 - 6

2х = 28

х = 28 : 2

х = 14 (см) – ширина прямокутника.

14 + 6 = 20 (см) – довжина прямокутника.

14 • 20 = 280 (см²) – площа прямокутника.

Відповідь: 280 см².

Знайдіть площу поверхні й об’єм прямокутного паралелепіпеда з вимірами 10 см, 5 см і 3 см.

Розв'язання

1) (5 • 3 + 5 • 10 + 10 • 3) • 2 = (15 + 50 + 30) • 2 = 95 • 2 = 190 (см²) – площа поверхні.

2) 5 • 3 • 10 = 150 (см³) – об'єм паралелепіпеда.

Відповідь: 190 см²; 150 см³.

Довжина алюмінієвого листа дорівнює 1,5 м, ширина — 80 см, а товщина — 3 мм. Знайдіть масу листа, якщо маса 1 см³ алюмінію дорівнює 2,7 г.

Розв'язання

1) 150 • 80 • 0,3 = 3600 (см³) – об'єм листа.

2) 3600 • 2,7 =  9720 (г) = 9,72 (кг) – маса листа.

Відповідь: 9,72 кг.

Місткість акваріума дорівнює 270 л. Знайдіть висоту акваріума, якщо його довжина дорівнює 9 дм, а ширина — 5 дм.

Розв'язання

1) 9 • 5 = 45 (дм²) – площа основи акваріума.

2) 270 : 45 =  6 (дм) – висота акваріума.

Відповідь: 6 дм.

Оксана хоче записати найбільший десятковий дріб, який був би меншим від 1. Чи зможе вона це зробити?  Ні, тому що кількість десяткових розрядів нескінченна.

Максим і Віктор заходять в автобус, у якому є 6 вільних місць. Скількома способами вони можуть розміститися на цих місцях?

Розв'язання

6 • 5 = 30 (сп.)

Відповідь: 30 способів.

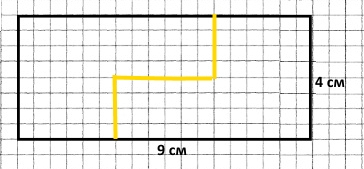
Прямокутник завдовжки 9 см і завширшки 4 см розбийте на дві частини так, щоб з них можна було скласти квадрат.

Розв'язання

1) 9 • 4 = 36 (дм²) – площа прямокутника.

2) 36 : 2 = 18 (дм²) – площа кожного квадрата.

Футбольна команда у 3 матчах забила 4 м’ячі і пропустила 1. Один із цих матчів вона виграла, один зіграла внічию й один програла. З яким рахунком закінчився переможний матч? Виграла 4 : 0, внічию 0 : 0, програла 0 : 1. Переможний матч з рахунком 4 : 0.