© Барна Р., 2021
Серія "Вчимось разом" до підручника
"Математика 4 клас Скворцова С., Онопрієнко О."
Сторінка 42
Завдання 4 Письмове ділення
|
_784 | 7 7 112 _7 7 +14 14 0 |
_856 | 4 8 214 _5 4 _16 16 0 |
_948 | 3 3 116 _4 3 _18 18 0 |
_798 | 7 7 114 _9 7 _28 28 0 |
_684 | 6 6 114 _8 6 _24 24 0 |
Завдання 5
1) Задачу на зведення до одиниці можна розв’язати тільки способом відношень
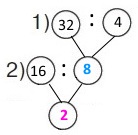
Перший катер зробив 6 рейсів, а другий — 3. Яку відстань подолав другий катер, якщо перший подолав 32 км? Кожного рейсу катери долали однакову відстань.
|
1 спосіб (відношень) Короткий запис І катер — 6 рейсів — 32 км ІІ катер — 3 рейси — ? км Вираз 32 : (6 : 3) План розв’язування 1) У скільки разів менше рейсів зробив ІІ катер? 2) Яку відстань подолав другий катер? Розв’язання 1) 6 : 3 = 2 (рази) – у стільки разів менше рейсів зробив ІІ катер. 2) 32 : 2 = (20 + 12) : 2 = 16 (км) – відстань подолав другий катер. |
2 спосіб (рівняння для відношень) Короткий запис І катер — 6 рейсів — 32 км ІІ катер — 3 рейси — х км Нехай х (км) – загальна відстань другого катера, тоді 6 : 3 (разів) – у стільки разів менше рейсів, а також х : 32 (км) – у стільки менше кілометрів, тому складемо рівняння 32 : х = 6 : 3 32 : х = 2 х = 32 : 2 = (20 + 12) : 2 = 16 (км) – відстань подолав другий катер. |
Відповідь: другий катер подолав 16 кілометрів.
2) Задачу на зведення до одиниці можна розв’язати двома способами (зведенням до одиниці і відношень)
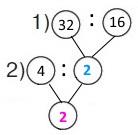
Два катери зробили однакову кількість рейсів. Перший катер подолав 32 км, кожного рейсу долаючи 4 км. Скільки кілометрів долав кожного рейсу другий катер, якщо всього він подолав 16 км?
|
1 спосіб (зведення до одиниці) Короткий запис І катер — 4 км — 32 км ІІ катер — ? — 16 км Схема
Вираз 16 : (32 : 4) План розв’язування 1) скільки рейсів зробив перший (другий) катер? 2) Скільки кілометрів долав кожного рейсу другий катер? Розв’язання 1) 32 : 4 = 8 (р.) – рейсів зробив перший (другий) катер. 2) 16 : 8 = 2 (км) – відстань долав кожного рейсу другий катер. |
2 спосіб (відношень) Короткий запис І катер — 4 км — 32 км ІІ катер — ? — 16 км Схема
Вираз 4 : (32 : 16) План розв’язування 1) У скільки разів менше кілометрів подолав другий катер? 2) Скільки кілометрів долав кожного рейсу другий катер? Розв’язання 1) 32 : 16 = 2 (рази) – у стільки разів менше кілометрів подолав другий катер. 2) 4 : 2 = 2 (км) – відстань долав кожного рейсу другий катер. |
|
3 спосіб (рівняння для зведення до одиниці) Короткий запис І катер — 4 км — 32 км ІІ катер — х км — 16 км Нехай х (км) – відстань другого катера за рейс, тоді 16 : х (р.) – кількість рейсів, а також 32 : 4 (р.) – кількість рейсів, тому складемо рівняння 16 : х = 32 : 4 16 : х = 8 х = 16 : 8 = 2 (км) – кілометрів долав кожного рейсу другий катер. |
4 спосіб (рівняння для відношень) Короткий запис І катер — 4 км — 32 км ІІ катер — х км — 16 км Нехай х (км) – відстань другого катера за рейс, тоді 32 : 16 (разів) – у стільки разів більша відстань, а також 4 : х (разів) – у стільки разів більша відстань за рейс, тому складемо рівняння 4 : х = 32 : 16 4 : х = 2 х = 4 : 2 = 2 (км) – кілометрів долав кожного рейсу другий катер. |
Відповідь: другий катер кожного рейсу долав 2 кілометри.
Завдання 6 Рівняння
|
y : 25 = 3 y = 3 • 25 y = 3 • (20 + 5) y = 75 75 : 25 = 3 3 = 3 |
7 • n = 420 • 2 7 • n = 840 n = 840 : 7 n = (700 + 140) : 7 n = 120 7 • 120 = 840 420 • 2 = 840 840 = 840 |
720 : (b • 2) = 9 b • 2 = 720 : 9 b • 2 = 80 b = 80 : 2 b = 40 720 : (40 • 2) = 720 : 80 = 9 9 = 9 |
297 : c = 99 : 33 297 : c = 3 c = 297 : 3 c = (270 + 27) : 3 c = 99 297 : 99 = 3 99 : 33 = 3 3 = 3 |
Завдання 7 Якщо майстриня зробить 3 однакові браслети, у мішечку з перлинами залишиться 96 перлин, а якщо зробить 5 таких браслетів, то в мішечку залишиться 28 перлин. Скільки перлин використовує майстриня на браслет?
|
Короткий запис №1 Було — однаково Зробила — 3 браслети по ? перлин Залишилося — 96 перлин |
Короткий запис №2 Було — однаково Зробила — 5 браслетів по ? перлин Залишилося — 28 перлин |
Розв’язання
1) 5 – 3 = 2 (б.) – різниця браслетів.
2) 96 – 28 = 96 – 30 + 2 = 68 (п.) – перлин іде на 2 браслети.
3) 68 : 2 = 34 (п.) – перлин використовує на браслет.
2 спосіб (рівняння)
|
Майстриня |
Було (однаково) |
Зробила |
Залишилося |
|
І |
96 + х • 3 |
3 браслети по х перлин |
96 перлин |
|
ІІ |
28 + х • 5 |
5 браслетів по х перлин |
28 перлин |
Якщо х (п.) – перлин використовує на браслет, тоді х • 3 + 96 (п.) – перлин у майстрині, а також х • 5 + 28 (п.) – перлин у майстрині. Складемо рівняння
х • 3 + 96 = х • 5 + 28
х • 5 + 28 = х • 3 = 96
х • 5 – х • 3 = 96 – 28
х • 2 = 68
х = 68 : 2 = 34 (п.) – перлин використовує на браслет.
Відповідь: на браслет майстриня використовує 34 перлини.
Сторінка 43
Завдання 1 Ділення з остачею
45 : 7 = 6 (ост. 3) перевірка 6 • 7 + 3 = 42 + 3 = 45
8 : 9 = 0 (ост. 8) перевірка 0 • 9 + 8 = 0 + 8 = 8
87 : 10 = 8 (ост. 7) перевірка 8 • 10 + 7 = 80 + 7 = 87
Завдання 2
|
_894 | 2 8 447 _9 8 _14 14 0 |
_675 | 3 6 225 _7 6 _15 15 0 |
_896 | 4 8 224 _9 8 _16 16 0 |
_575 | 5 5 115 _7 5 _25 25 0 |
Завдання 4
|
_996 | 6 6 166 _39 36 _36 36 0 |
_708 | 4 4 177 _30 28 _28 28 0 |
_938 | 7 7 134 _23 21 _28 28 0 |
_780 | 5 5 156 _28 25 _30 30 0 |
|
_896 | 7 7 128 _19 14 _56 56 0 |
_976 | 4 8 244 _17 16 _16 16 0 |
_471 | 3 3 157 _17 15 _21 21 0 |
_861 | 7 7 123 _16 14 _21 21 0 |
Спільне: число сотень не можна розділити на дільник націло.
Завдання 5
1) Задачу на зведення до одиниці можна розв’язати тільки способом зведення до одиниці (не можна розв'язати способом відношень)
5 волоських горіхів важать 100 г. Скільки волоських горіхів у пакеті масою 280 г?
|
1 спосіб (зведення до одиниці) Короткий запис 5 горіхів — 100 г ? горіхів — 280 г План розв’язування 1) Яка маса горіха? 2) Скільки волоських горіхів у пакеті? Розв’язання 1) 100 : 5 = 20 (г) — маса одного горіха. 2) 280 : 20 = 14 (г.) — волоських горіхів у пакеті. |
2 спосіб (рівняння для зведення до одиниці) Короткий запис 5 горіхів — 100 г х горіхів — 280 г Нехай х (г.) – волоських горіхів у пакеті, тоді 100 : 5 (г) – маса горіха, а також 280 : х (г) – маса горіха, тоді складемо рівняння 280 : х = 100 : 5 280 : х = 20 х = 280 : 20 = 28 : 2 = 14 (г.) – волоських горіхів у пакеті. |
Відповідь: у пакеті 14 волоський горіхів.
Сторінка 44
2) Задачу на зведення до одиниці можна розв’язати тільки способом відношень
Маса 45 мигдалевих горіхів становить 50 г. Скільки мигдалевих горіхів у пакеті масою 200 г?
|
1 спосіб (відношень) Короткий запис 45 горіхів — 50 г ? горіхів — 200 г Вираз 45 • (200 : 50) План розв’язування 1) У скільки разів більша загальна маса горіхів? 2) Скільки мигдалевих горіхів у пакеті? Розв’язання 1) 200 : 50 = 4 (рази) – у стільки разів більша загальна маса горіхів. 2) 45 • 4 = (40 + 5) • 4 = 180 (г.) – мигдалевих горіхів у пакеті. |
2 спосіб (рівняння для відношень) Короткий запис 45 горіхів — 50 г х горіхів — 200 г Нехай х (г.) – горіхів у пакеті, тоді 200 : 50 (разів) – у стільки разів більша загальна маса, а також х : 45 (разів) – у стільки разів більше горіхів у пакеті, тому складемо рівняння х : 45 = 200 : 50 х : 45 = 4 х = 4 • 45 = 4 • (40 + 5) = 180 (г.) – мигдалевих горіхів у пакеті. |
Відповідь: у пакеті 180 мигдалевих горіхів.
Завдання 6
1) Задачу на зведення до одиниці можна розв’язати тільки способом відношень
Маса 25 зерняток льону становить З г. Скільки зерняток міститься в 12 г льону?
|
1 спосіб (відношень) Короткий запис 3 г — 25 зерняток 12 г — ? зерняток Вираз 45 • (200 : 50) План розв’язування 1) У скільки разів більша загальна маса зерняток? 2) Скільки зерняток міститься у пакеті? Розв’язання 1) 12 : 3 = 4 (рази) – у стільки разів більша загальна маса зерняток. 2) 25 • 4 = (20 + 5) • 4 = 100 (з.) – зерняток у дванадцяти грамах льону. |
2 спосіб (рівняння для відношень) Короткий запис 3 г — 25 зерняток 12 г — х зерняток Нехай х (з.) – зерняток у пакеті, тоді 12 : 3 (разів) – у стільки разів більша загальна маса, а також х : 45 (разів) – у стільки разів більше зерняток, тому складемо рівняння х : 25 = 12 : 3 х : 25 = 4 х = 4 • 25 = 4 • (20 + 5) = 100 (з.) – зерняток міститься. |
Відповідь: міститься 100 зерняток.
2) Обернену задачу на зведення до одиниці можна розв’язати тільки способом відношень
Маса 25 зерняток льону становить З г. Яка маса 100 зерняток?
|
1 спосіб (відношень) Короткий запис 3 г — 25 зерняток ? г — 100 зерняток Вираз 3 • (100 : 25) План розв’язування 1) У скільки разів більше зерняток? 2) Яка маса 100 зерняток? Розв’язання 1) 100 : 25 = 4 (рази) – у стільки разів більше зерняток. 2) 3 • 4 = 12 (г) – маса 100 зерняток. |
2 спосіб (рівняння для відношень) Короткий запис 3 г — 25 зерняток х г — 100 зерняток Нехай х (г) – маса ста зерняток, тоді 100 : 25 (разів) – у стільки разів більше зерняток, а також х : 3 (разів) – у стільки разів більша маса зерняток, тому складемо рівняння х : 3 = 100 : 25 х : 3 = 4 х = 4 • 3 = 12 (г) – маса ста зерняток. |
Відповідь: маса ста зерняток 12 г.
Завдання 7
|
х : 24 + 499 = 501 х : 24 = 501 – 499 х : 24 = 501 – 500 + 1 = 2 х = 2 • 24 х = 48 48 : 24 + 499 = 48 : 8 : 3 + 499 = 501 501 = 501 |
360 : х + 798 = 801 360 : х = 801 – 798 360 : х = 801 – 800 + 2 360 : х = 3 х = 360 : 3 х = 120 360 : 120 + 798 = 3 + 798 = 801 801 = 801 |
|
480 : 240 – х = 2 480 : 80 : 3 – х = 2 2 – х = 2 х = 2 – 2 х = 0 480 : 240 – 0 = 48 : 24 – 0 = 2 2 = 2 |
107 • 6 – х = 42 642 – х = 42 х = 642 – 42 х = 600 107 • 6 – 600 = 642 – 600 = 42 42 = 42 |
Завдання 8 Порядок дій
145 – (19 + 53) : 6 + 139 – (58 + 33) : 7 = 259
1) 19 + 53 = 53 + 7 + 12 = 60 + 12 = 72
2) 58 + 33 = 80 + 11 = 91
3) 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12
4) 91 : 7 = (70 + 21) : 7 = 10 + 3 = 13
5) 145 – 12 = 133
6) 133 + 139 – 13 = 133 – 13 + 139 = 120 + 139 = 259
Сторінка 45
Завдання 1
208 : 52 • 180 : 60 • 80 : 4 – 354 : 59 • 140 : 21 = 200
1) 208 : 52 = 4
2) 4 • 180 = 4 • (100 + 80) = 400 + 320 = 720
3) 720 : 60 = 72 : 6 = (60 + 12) : 6 = 10 + 2 = 12
4) 12 • 80 = (10 + 2) • 80 = 800 + 160 = 960
5) 960 : 4 = (800 + 160) : 4 = 200 + 40 = 240
6) 354 : 59 = 6
7) 6 • 140 = 6 • (100 + 40) = 600 + 240 = 840
8) 840 : 21 = 840 : (7 • 3) = 840 : 7 : 3 = 120 : 3 = 40
9) 240 – 40 = 200
Завдання 2 Розподільний закон ділення відносно додавання
154 : 7 = (140 + 14) : 7 = 140 : 7 + 14 : 7 = 20 + 2 = 22
904 : 8 = (800 + 80 + 24) : 8 = 100 + 10 + 3 = 113
345 : 5 = (300 + 45) : 5 = 60 + 5 = 65
129 : 3 = (120 + 9) : 3 = 40 + 3 = 43
|
Вираз |
154 : 7 |
904 : 8 |
345 : 5 |
129 : 3 |
|
Перше неповне ділене |
14 |
9 |
30 |
12 |
|
2 |
3 |
2 |
2 |
Завдання 3
|
Вираз |
804 : 4 |
342 : 6 |
728 : 8 |
963 : 3 |
|
Перше неповне ділене |
8 |
30 |
72 |
9 |
|
Кількість цифр у частці |
3 |
2 |
2 |
3 |
Завдання 4
|
Вираз |
976 : 4 |
376 : 4 |
|
Перше неповне ділене |
9 |
37 |
|
Кількість цифр у частці |
3 |
2 |
Сторінка 46
Вправа 5 Спільне: однакова кількість цифр у частці
|
Вираз |
265 : 5 |
656 : 8 |
238 : 7 |
783 : 9 |
|
Перше неповне ділене |
26 |
65 |
23 |
78 |
|
Кількість цифр у частці |
2 |
2 |
2 |
2 |
|
Письмове ділення |
_265 | 5 25 53 _15 15 0 |
_656 | 8 64 82 _16 16 0 |
_238 | 7 21 34 _28 28 0 |
_783 | 9 72 87 _63 63 0 |
|
Вираз |
819 : 9 |
276 : 4 |
474 : 6 |
165 : 5 |
|
Перше неповне ділене |
81 |
27 |
47 |
16 |
|
Кількість цифр у частці |
2 |
2 |
2 |
2 |
|
Письмове ділення |
_819 | 9 81 91 _9 9 0 |
_276 | 4 24 69 _36 36 0 |
_474 | 6 42 79 _54 54 0 |
_165 | 5 15 33 _15 15 0 |
Завдання 6
|
Вираз |
375 : 5 |
768 : 4 |
183 : 3 |
756 : 9 |
|
Перше неповне ділене |
37 |
7 |
18 |
75 |
|
Кількість цифр у частці |
2 |
3 |
2 |
2 |
|
Письмове ділення |
_375 | 5 35 75 _25 25 0 |
_768 | 4 4 192 _36 36 _8 8 0 |
_183 | 3 18 61 _3 3 0 |
_756 | 9 72 84 _36 36 0 |
|
Вираз |
904 : 8 |
588 : 7 |
868 : 7 |
952 : 7 |
|
Перше неповне ділене |
9 |
58 |
86 |
9 |
|
Кількість цифр у частці |
3 |
2 |
2 |
3 |
|
Письмове ділення |
_904 | 8 8 113 _10 8 _24 24 0 |
_588 | 7 56 84 _28 28 0 |
_868 | 7 7 124 _16 14 _28 28 0 |
_952 | 7 7 136 _25 21 _42 42 0 |
Завдання 7
1) Задачу зведення до одиниці можна розв’язати двома способами
За 8 год яхта витратила 240 л пального. Скільки літрів пального потрібно цій яхті на 16 год ходу, якщо щогодини вона витрачає однакову кількість пального?
|
1 спосіб (зведення до одиниці) Короткий запис 8 год — 240 л 16 год — ? л План розв’язування 1) Скільки літрів пального витрачає щогодини? 2) Скільки літрів пального потрібно на 16 год ходу? 1) 240 : 8 = 30 (л) — літрів пального витрачає щогодини. 2) 16 • 30 = (10 + 6) • 30 = 480 (л) — літрів пального треба на 16 год ходу. |
2 спосіб (відношень) Короткий запис 8 год — 240 л 16 год — ? л План розв’язування 1) У скільки разів більше годин? 2) Скільки літрів пального потрібно на 16 год ходу? 1) 16 : 8 = 2 (рази) – у стільки разів більше годин. 2) 240 • 2 = 240 + 240 = 480 (л) — літрів пального треба на 16 год ходу. |
|
3 спосіб (рівняння для зведення до одиниці) Короткий запис 8 год — 240 л 16 год — х л Нехай х (л) – треба літрів пального, тоді х : 16 (л) – витрати щогодини, а також 240 : 8 (л) – витрати щогодини, тому складемо рівняння х : 16 = 240 : 8 х : 16 = 30 х = 30 • 16 = 30 • (10 + 6) = 480 (л) – літрів пального треба. |
4 спосіб (рівняння для відношень) Короткий запис 8 год — 240 л 16 год — х л Нехай х (л) – треба літрів пального, тоді 16 : 8 (разів) – у стільки разів більше годин, а також х : 240 (разів) – у стільки разів більше літрів, тому складемо рівняння х : 240 = 16 : 8 х : 240 = 2 х = 2 • 240 = 240 + 240 = 480 (л) – літрів пального треба. |
Відповідь: цій яхті потрібно 480 літрів пального.
2) Обернену задачу на зведення до одиниці можна розв’язати двома способами
За 8 год яхта витратила 240 л пального. За скільки годин ходу яхта витратить 480 л пального, якщо щогодини вона витрачає однакову кількість пального?
|
1 спосіб (зведення до одиниці) Короткий запис 8 год — 240 л ? год — 480 л План розв’язування 1) Скільки літрів пального витрачає щогодини? 2) За скільки годин ходу витратить 480 л пального? 1) 240 : 8 = 30 (л) — літрів пального витрачає щогодини. 2) 480 : 30 = (300 + 180) : 30 = 16 (год) — годин ходу потрібно. |
2 спосіб (відношень) Короткий запис 8 год — 240 л х год — 480 л План розв’язування 1) У скільки разів більше літрів? 2) За скільки годин ходу яхта витратить 480 л пального? 1) 480 : 240 = 2 (рази) – у стільки разів більше літрів пального. 2) 8 • 2 = 16 (год) — годин ходу потрібно. |
|
3 спосіб (рівняння для зведення до одиниці) Короткий запис 8 год — 240 л х год — 480 л Нехай х (год) – годин ходу потрібно, тоді 480 : х (л) – витрати щогодини, а також 240 : 8 (л) – витрати щогодини, тому складемо рівняння 480 : х = 240 : 8 480 : х = 30 х = 480 : 30 = (300 + 180) : 30 = 16 (год) – годин ходу потрібно. |
4 спосіб (рівняння для відношень) Короткий запис 8 год — 240 л х год — 480 л Нехай х (год) – годин ходу треба, тоді 480 : 240 (разів) – у стільки разів більше літрів, а також х : 8 (разів) – у стільки разів більше годин, тому складемо рівняння х : 8 = 480 : 240 х : 8 = 2 х = 2 • 8 = 16 (год) – годин ходу потрібно. |
Відповідь: потрібно 16 годин ходу.
Завдання 8
|
632 : 4 • 3 – 287 = 123 (369 : 3 – 95) • 8 = 224 |
_632 | 4 4 158 _23 20 _32 32 0 |
х158 3 474 |
_474 287 187 |
_369 | 3 3 123 _6 6 _9 9 0 |
_123 95 28 |
х28 8 224 |
|
148 • 3 : 6 + 567 = 641 (486 + 27 • 7) : 5 = 135 |
х148 3 444 |
_444 | 6 42 74 _24 24 0 |
+567 74 641 |
х27 7 189 |
+486 189 675 |
_675 | 5 5 135 _17 15 _25 25 0 |
|
978 : 3 : 2 – 89 = 74 (512 – 651 : 3) • 5 = 1475 |
_978 | 3 9 326 _7 6 _18 18 0 |
_326 | 2 2 163 _12 12 _6 6 0 |
_163 89 74 |
_651 | 3 6 217 _5 3 _21 21 0 |
_512 217 295 |
х295 5 1475 |
Завдання 9 За три дні яхта подолала 24 милі. Другого дня — у 2 рази більше, ніж першого, а третього — у 5 разів більше, ніж першого. Скільки миль долала яхта щодня?
Короткий запис
І дня — ?
ІІ дня — ?, у 2 рази більше, ніж І дня
ІІІ дня — ?, у 5 разів більше, ніж І дня
Всього — 24 милі
Розв’язання
Якщо другого дня у 2 рази більше від першого, а третього – у 5 разів більше від першого дня, тоді на перший день припадає 1 частина, на другий – 2 таких частини, на третій – 5 таких частин, тоді
1) 1 + 2 + 5 = 8 (частин) – всього однакових частин.
2) 24 : 8 = 3 (м) – миль долала І дня (одна частина).
3) 3 • 2 = 6 (м) – миль долала ІІ дня (дві частини).
4) 3 • 5 = 15 (м) – миль долала ІІІ дня (п’ять частин).
2 спосіб (рівняння)
Нехай х (м) – миль долала І дня, тоді х • 2 (м) – миль долала ІІ дня, х • 5 (м) – миль долала ІІІ дня, складемо рівняння
х + х • 2 + х • 5 = 24
х • 1 + х • 2 + х • 5 = 24
х • (1 + 2 + 5) = 24
х • 8 = 24
х = 24 : 8
х = 3 (м) – миль долала І дня.
Х • 2 = 3 • 2 = 6 (м) – миль долала ІІ дня.
Х • 5 = 3 • 5 = 15 (м) – миль долала ІІІ дня.
Відповідь: І дня – 3 милі, ІІ дня – 6 миль, ІІІ дня – 15 миль.