© ГДЗ 8next.com, 2013, 2018, 2022
Питання
1 3 яких фігур складається поверхня прямокутного паралелепіпеда? Поверхня прямокутного паралелепіпеда складається з прямокутників.
2 Скільки прямокутний паралелепіпед має граней? вершин? ребер?. Прямокутний паралелепіпед має 6 граней. 8 вершин і 12 ребер.
3. Які є назви вимірів прямокутного паралелепіпеда? Ширина, довжина, висота.
4. Яку фігуру називають кубом? Прямокутний паралелепіпед, у якого всі виміри рівні, називають кубом.
5. З яких фігур складається поверхня куба? Поверхня куба складається з квадратів.
Розв’язуємо усно
Завдання 1
1) 13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1300
2) 4 • 5 • 78 • 5 = (4 • 5 • 5) • 78 = 100 • 78 = 7800
3) 125 • 943 • 8 = 25 • 5 • 943 • 4 • 2 = (25 • 4) • (5 • 2) • 943 = 100 • 10 • 943 = 943000
Завдання 2 Спростіть вираз.
1) 3а • 16b = (3 • 16) • аb = 48аb
2) 4m • 9n • 5k = (4 • 5 • 9) • mnk = 180mnk
3) 7а • 2b • 50с • 8d = (7 • 8) • (2 • 50) • аbсd = 56 • 100 • аbсd = 5600аbсd
Завдання 3 Розкрийте дужки.
1) 2 (а + b) = 2а + 2b
2) (3 – b) • 5 = 3 • 5 – b • 5 = 15 – 5b
3) 6m (7n + 8р) = 6 • 7 • mn + 6 • 8 • mр = 42mn + 48mр
Завдання 4 Знайдіть периметр прямокутника, площа якого дорівнює 28 см2, а одна з його сторін — 7 см.
Розв’язання
1) 28 : 7 = 4 (см) – друга сторона.
2) Р = (7 см + 4 см) • 2 = 22 см – периметр прямокутника.
Відповідь: периметр прямокутника дорівнює 22 см.
Завдання 5 У магазині розклали 6 ц яблук по ящиках так, що в кожному ящику міститься по 12 кг яблук. Скільки ящиків заповнили яблуками?
Розв’язання
6 ц = 600 кг
600 : 12 = 50 (ящ.) – ящиків заповнили яблуками.
Відповідь: яблуками заповнили 50 ящиків.
Завдання 6 У скільки разів площа квадрата зі стороною 6 см більша за площу квадрата зі стороною 2 см?
Розв’язання
1) 6 • 6 = 36 (см2) – площа квадрата зі стороною 6 см.
2) 2 • 2 = 4 (см2) – площа квадрата зі стороною 2 см.
3) 36 : 4 = 9 (разів) – у стільки разів більша площа квадрата зі стороною 6 см
Відповідь: площа квадрата зі стороною 6 см у 9 разів більша, ніж площа квадрата зі стороною 2 см.
Вправи
Вправа 633° На рисунку 178 зображено прямокутний паралелепіпед MNKPEFST. Назвіть:
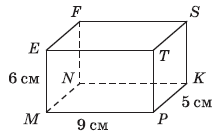
1) ребра, які є сторонами грані EFST; EF, FS, ST, TE
2) грані, яким належить вершина K; PTSK, MNKP, NFSK
3) ребра, які дорівнюють ребру NK; MP, ET, FS
4) грані, які мають спільне ребро ME; MEFN, METP
5) грань, яка дорівнює грані PTSK. MEFN
Вправа 634° На грані куба сидить сонечко (рис. 179). Назвіть грань куба, на якій воно сидить, якщо ви:
1) бачите сонечко; a) MNKP, б) AMPD
2) не бачите його. а) BNKC, б) AMNB
Вправа 635° На рисунку 178 виміри прямокутного паралелепіпеда MNKPEFST дорівнюють 9 см, 5 см і 6 см. Обчислили:
Розв’язання
1) 9 • 5 = 45 см2 – площа грані MNKP.
2) 9 • 6 = 54 см2 – площа грані NFSK.
3) (6 см • 5 см) • 2 + (9 см • 5 см) • 2 + (9 см • 6 см) • 2 = 60 см2 + 90 см2 + 108 см2 = 258 см2 – площа поверхні прямокутного паралелепіпеда.
4) 6 см • 4 + 9 см • 4 + 5 см • 4 = (6 см + 9 см + 5 см) • 4 = 80 см – сума довжин усіх ребер прямокутного паралелепіпеда.
Вправа 636° Знайдіть суму довжин усіх ребер і площу поверхні прямокутного паралелепіпеда, виміри якого дорівнюють 7 см, 10 см і 11 см.
Розв’язання
1) (10 см + 7 см + 11 см) • 4 = 28 см • 4 = 112 см – сума довжин усіх ребер прямокутного паралелепіпеда.
2) (7 м • 10 м) • 2 + (7 м • 11 м) • 2 + (10 м • 11 м) • 2 =
= (70 м2 + 77 м2 + 110 м2) • 2 = 257 м2 • 2 = 514 м2 – площа поверхні прямокутного паралелепіпеда.
Відповідь: площа поверхні прямокутного паралелепіпеда дорівнює 514 м2.
Вправа 637° (Домашня практична робота) Знайдіть удома предмет, який має форму прямокутного паралелепіпеда. Виконайте потрібні вимірювання та обчисліть площу його поверхні. Виміри шафи-пеналу дорівнюють 2 м, 1 м і 4 дм
Розв’язання
2 м = 20 дм, 1 м = 10 дм
(20 дм • 10 дм) • 2 + (20 дм • 4 дм) • 2 + (10 дм • 4 дм) • 2 =
= (200 дм2 + 80 дм2 + 40 дм2) • 2 = 320 дм2 • 2 = 640 дм2 – площа поверхні прямокутного паралелепіпеда.
Відповідь: площа поверхні прямокутного паралелепіпеда дорівнює 640 дм2.
Вправа 638° Площа грані куба дорівнює 9 см2. Чому дорівнює площа поверхні куба?
У куба всі шість граней рівні.
9 • 6 = 54 см2 – площа поверхні куба.
Відповідь: площа поверхні куба дорівнює 54 см2.
Вправа 639° Обчисліть площу поверхні та суму довжин усіх ребер куба, ребро якого дорівнює 5 см.
Розв’язання
У куба всі дванадцять ребер рівні і всі шість граней рівні.
1) 5 • 12 = 60 (см) – сума довжин усіх ребер куба.
2) 5 • 5 = 25 (см2) – площа одної грані.
3) 25 • 6 = 150 (см2) – площа поверхні куба.
Відповідь: сума довжин усіх граней куба дорівнює 60 см, площа поверхні – 150 см2.
Вправа 640° Знайдіть суму довжин усіх ребер і площу поверхні куба, ребро якого дорівнює 7 см.
Розв’язання
У куба всі дванадцять ребер рівні і всі шість граней рівні.
1) 7 • 12 = 84 (см) – сума довжин усіх ребер куба.
2) 7 • 7 = 49 (см2) – площа одної грані.
3) 49 • 6 = 294 (см2) – площа поверхні куба.
Відповідь: сума довжин усіх ребер куба дорівнює 84 см, площа поверхні – 294 см2.
Вправа 641° На рисунку 180 зображено піраміду МАВС. Укажіть:
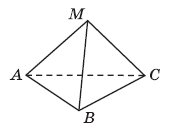
1) основу піраміди;
2) вершину піраміди;
3) бічні грані піраміди;
4) бічні ребра піраміди;
5) ребра основи піраміди.
Розв’язання
1) ABC
2) M
3) AМM, BМС, AМС
4) AM, BM, CM
5) AB, BC, СА
Вправа 642° На рисунку 181 зображено піраміду SABCD. Укажіть:
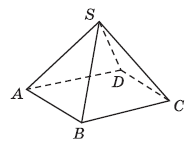
1) основу піраміди;
2) вершину піраміди;
3) бічні грані піраміди;
4) бічні ребра піраміди;
5) ребра основи піраміди.
Розв’язання
1) ABCD
2) S
3) ABS, BCS, CDS, DAS
4) AS, BS, CS, DS
5) AB, BC, CD, DA
Вправа 643 На рисунку 182 зображено розгортку прямокутного паралелепіпеда.
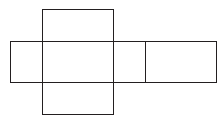
1) Зі скількох прямокутників складається розгортка?
2) Скільки пар рівних прямокутників містить розгортка?
3) Яка площа цієї розгортки, якщо виміри паралелепіпеда дорівнюють 10 см, 7 см і 3 см?
Розв’язання
1) з 6 граней.
2) 3 пари рівних прямокутників.
3) (10 см • 7 см) • 2 + (7 см • 3 см) • 2 + (10 см • 3 см) • 2 =
= 140 см2 + 42 см2 + 60 см2 = 242 см2 – площа розгортки.
Вправа 644 Обчисліть площу поверхні прямокутного паралелепіпеда, розгортку якого зображено на рисунку
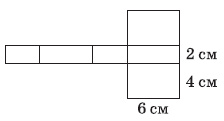
Розв’язання
(6 см • 4 см) • 2 + (6 см • 2 см) • 2 + (2 см • 4 см) • 2 =
= 48 см2 + 24 см2 + 16 см2 = 88 см2 – площа поверхні розгортки прямокутного паралелепіпеда.
Відповідь: площа поверхні розгортки 88 см2.
Вправа 645 Сума довжин усіх ребер прямокутного паралелепіпеда дорівнює 28 см. Знайдіть суму довжин трьох його ребер, що мають спільну вершину.
Розв’язання
Прямокутний паралелепіпед має 4 пари рівних ребер, тому
28 : 4 = 7 (см) – сума вимірів трьох ребер, що мають спільну вершину.
Відповідь: сума довжин трьох ребер, що виходять з одної вершини, дорівнює 7 см.
Вправа 646 Сума довжин усіх ребер куба дорівнює 72 см. Знайдіть довжину ребра куба.
Розв’язання
Куб має 12 рівних ребер, тому
72 : 12 = 6 (см) – довжина кожного ребра.
Відповідь: довжина ребра куба дорівнює 6 см.
Вправа 647 Піраміда має 1001 грань. Скільки:
1) сторін має основа піраміди; 1001
2) ребер має ця піраміда? 2002
Вправа 648 Основою піраміди є двадцятикутник. Знайдіть кількість граней піраміди та кількість її ребер.
Розв’язання
1) 20 + 1 = 21 (шт.) – граней має двадцятикутна піраміда.
2) 20 • 2 = 40 (шт.) – ребер має двадцятикутна піраміда.
Відповідь: двадцятикутна піраміда має 21 грань і 40 ребер.
Вправа 649 Прямокутний паралелепіпед і куб мають рівні площі поверхні. Ребро куба дорівнює 8 см, а два виміри прямокутного паралелепіпеда — 4 см і 12 см. Знайдіть третій вимір паралелепіпеда.
Розв’язання
1) 8 • 8 • 6 = 384 (см2) – площа поверхні куба або прямокутного паралелепіпеда.
2) 12 • 4 • 2 = 96 (см2) – площа поверхні двох граней прямокутного паралелепіпеда.
3) 384 – 96 = 288 (см2) – площа поверхні решта граней прямокутного паралелепіпеда.
4) Нехай х невідомий вимір. Складаємо рівняння.
(4х + 12х) • 2 = 288
16х = 288 : 2
16х = 144
х = 144 : 16
х = 9 (см)
Відповідь: невідомий вимір паралелепіпеда дорівнює 9 см.
Вправа 650 Прямокутний паралелепіпед і куб мають рівні площі поверхні. Довжина паралелепіпеда дорівнює 18 м, що у 2 рази більше, ніж його ширина, і на 8 м більше, ніж його висота. Знайдіть ребро куба.
Розв’язання
1) 18 : 2 = 9 (м) – ширина прямокутного паралелепіпеда.
2) 18 – 8 = 10 (м) – висота прямокутного паралелепіпеда.
3) (18 м • 9 м) • 2 + (18 м • 10 м) • 2 + (9 м • 10 м) • 2 = 324 м2 + 360 м2 + 180 м2 = 864 м2 – площа поверхні паралелепіпеда або куба.
4) 864 : 6 = 144 (см) – площа однієї поверхні куба.
5) Оскільки 144 = 12 • 12, тому 12 (м) – сторона квадрата або шукане ребро куба.
Відповідь: ребро куба дорівнює 12 м.
Вправа 651 Брусок, що має форму прямокутного паралелепіпеда з вимірами 4 см, 5 см і 6 см, пофарбували з усіх сторін і розрізали на кубики з ребром 1 см. Скільки утворилося кубиків, у яких пофарбовано: 1) три грані; 2) дві грані; 3) одну грань?
Розв’язання
1) пофарбовані три грані будуть мати 8 кубиків.
Пояснення. Кубики при кожній вершині.
2) пофарбовані дві грані будуть мати 36 кубиків.
Пояснення. Дві грані будуть мати кубики при ребрах паралелепіпеда, крім тих, що знаходяться у вершинах паралелепіпеда. Біля ребра 4 см таких кубиків буде 4 – 2 = 2. Біля ребра 5 см таких кубиків буде 5 – 2 = 3. Біля ребра 6 см таких кубиків буде 6 – 2 = 4.
Візьмемо до уваги, однакових граней в паралелепіпеда по 4, тоді (2 + 3 + 4) • 4 = 36 кубиків.
3) пофарбовану грань будуть мати 52 кубики.
Пояснення. Одну пофарбовану грань будуть мати кубики всередині кожної грані паралелепіпеда, що не торкаються його граней. На грані з вимірами 4 см і 5 см кубиків, що не торкаються ребер паралелепіпеда, буде 2 • 3 = 6. На грані з вимірами 4 см і 6 см кубиків, що не торкаються ребер паралелепіпеда буде 2 • 4 = 8. На грані з вимірами 5 см і 6 см кубиків, що не торкаються ребер паралелепіпеда буде 3 • 4 = 12. Усього таких кубиків на гранях 6 + 8 + 12 = 26, а беручи до уваги, що грані попарно рівні, маємо 26 • 2 = 52
Вправи для повторення.
Вправа 653 Швидкість ракети дорівнює 8 км/с. За скільки хвилин вона пролетить 960 км?
Короткий запис
v — 8 км/с
t — 960 rv
S — ?
Розв’язання
S = v : t = 960 : 8 = (800 + 160) : 8 = 100 + 20 = 120 (с) = 2 (хв.) – потрібен час для ракети.
120 c = 2 • 60 c = 2 хв
Відповідь: 960 км ракета пролетить за 2 хв.
Вправа 654 Ділення з остачею
З листа картону можна вирізати шість однакових квадратів. Скільки листів картону потрібно для того, щоб вирізати 50 таких квадратів?
Короткий запис
1 лист картону – 6 квадратів
х листів картону – 50 квадратів
Розв’язання
50 : 6 = 8 (ост. 2) ≈ 9 (л.) – листів картону потрібно.
Відповідь: щоб вирізати 50 таких квадратів, треба 9 листів картону.
Вправа 655 Поїзд вийшов зі станції о 16 год зі швидкістю 54 км/год. О 19 год з цієї ж станції у протилежному напрямі вийшов другий поїзд. О 24 год відстань між поїздами становила 642 км. З якою швидкістю рухався другий поїзд?
Розв’язання.
1) 24 – 16 = 8 (год) – час у дорозі першого поїзда.
2) 54 • 8 = 432 (км) – відстань проїхав перший поїзд.
3) 642 – 432 = 210 (км) – відстань другого поїзда.
4) 24 – 19 = 5 (год) – час у дорозі другого поїзда.
5) 210 : 5 = 42 (км/год) – швидкість другого поїзда.
Відповідь: швидкість другого поїзда 42 км/год.
Вправа 656 Розв’яжіть рівняння:
|
1) 23х – 19х + 5х = 1827 9х = 1827 х = 1827 : 9 х = (1800 + 27) : 9 = 200 + 3 х = 203
|
2) 5х + Зх – 47 = 6401. 8х – 47 = 6401 8х = 6401 + 47 8х = 6448 х = 6448 : 8 х = (6400 + 48) : 8 = 800 + 6 х = 806 |
Задача від Мудрої Сови
Вправа 657
Дерев’яний брусок має форму прямокутного паралелепіпеда. Його ширина дорівнює 20 см, що на 5 см менше від його довжини та в 3 рази менше від його висоти. Скільки лаку потрібно, щоб одним шаром покрити ним усю поверхню цього бруска, якщо на 1 дм2 витрачається 4 г лаку?
Розв’язання
1) 20 + 5 = 25 (см) – довжина прямокутного паралелепіпеда.
2) 20 • 3 = 60 (см) – висота прямокутного паралелепіпеда.
3) (20 см • 25 см) • 2 + (20 см • 60 см) • 2 + (25 см • 60 см) • 2 =
= 1000 см2 + 2400 см2 + 3000 см2 = 6400 см2 – площа поверхні паралелепіпеда.
6400 см2 = 64 • 10 см • 10 см = 64 • 1 дм • 1 дм = 64 дм2
4) 4 • 64 = 256 (г) – грамів лаку потрібно.
Відповідь: 256 грамів лаку потрібно.
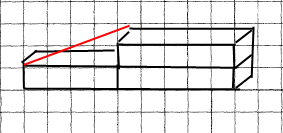
Задача 659 Як за допомогою лінійки виміряти діагональ цеглини, маючи ще кілька таких цеглин?
Розв’язання
Діагональ цеглини — це діагональ прямокутного паралелепіпеда. Діагональ паралелепіпеда — це відрізок, що сполучає його вершини, які не належать одній грані
----------------------- у підручниках за 2013, 2018 роки -------------------------------
Питання
1. Які предмети дають уяву про прямокутний паралелепіпед? Форму прямокутного паралелепіпеда мають, наприклад, коробка цукерок, книга, цеглина, коробка сірників, пакувальний ящик, пакет молока, дитячі кубики.
4. Скільки пар протилежних граней має прямокутний паралелепіпед? 3 пари протилежних граней.
5. Яку властивість мають протилежні грані прямокутного паралелепіпеда? Протилежні грані прямокутного паралелепіпеда рівні.
6. Як називають сторони граней прямокутного паралелепіпеда? Сторони граней прямокутного паралелепіпеда називають ребра.
7. Як називають вершини граней прямокутного паралелепіпеда? Вершини граней називають вершинами прямокутного паралелепіпеда.
8. Скільки вершин має прямокутний паралелепіпед? Прямокутний паралелепіпед має 8 вершин.
9. Скільки ребер має прямокутний паралелепіпед? Прямокутний паралелепіпед має 12 ребер.
10. Яка спільна назва довжин трьох ребер прямокутного паралелепіпеда, що мають спільну вершину? Виміри прямокутного паралелепіпеда.
11. Які назви вимірів прямокутного паралелепіпеда використовують, щоб їх розрізняти? Назви вимірів прямокутного паралелепіпеда: довжина, ширина, висота.
14. 3 яких фігур складається поверхня піраміди? Поверхня піраміди складається з многокутника та трикутників.
15. Яку піраміду називають трикутною? чотирикутною? Трикутною пірамідою називають піраміду, основою якої є трикутник. Чотирикутною пірамідою називають піраміду, основою якої є чотирикутник.
16. Що називають вершиною піраміди? Спільну вершину бічних граней називають вершиною піраміди.
17. Що називають ребрами основи піраміди? Сторони основи піраміди називають ребрами основи піраміди.
18. Що називають бічними ребрами піраміди? Сторони бічних граней піраміди, які не належать основі, називають бічними ребрами піраміди.
Вправа 613.* Висота прямокутного паралелепіпеда дорівнює 20 см, що на 5 см більше за його ширину та в 3 рази менше від його довжини. Обчисліть площу поверхні паралелепіпеда.
Розв’язання
1) 20 – 5 = 15 (см) – ширина прямокутного паралелепіпеда.
2) 20 • 3 = 60 (см) – довжина прямокутного паралелепіпеда.
3) (20 см • 15 см) • 2 + (20 см • 60 см) • 2 + (15 см • 60 см) • 2 =
= 600 см2 + 2400 см2 + 1800 см2 = 4800 см2 – площа поверхні паралелепіпеда.
Відповідь: площа поверхні паралелепіпеда 4800 см2.
Вправа 607° На рисунку 167 зображено прямокутний паралелепіпед ABCDMNKP. Назвіть:
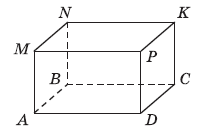
1) грані, яким належить вершина С;
2) ребра, що дорівнюють ребру ВС;
3) верхню грань;
4) вершини, що належать нижній грані;
5) грані, що мають спільне ребро AM;
6) грань, що дорівнює грані DPKC.
Розв’язання
1) ABCD, DPKC, BNKC
2) AD, MP, NK
3) MNKP
4) A, B, C, D
5) AMPD, AMNB
6) AMNB
Вправа 636° Знайдіть суму довжин усіх ребер прямокутного паралелепіпеда, виміри якого дорівнюють 13 см, 16 см, 21 см.
(13 см + 16 см + 21 см) • 4 = 50 см • 4 = 200 см – сума довжин усіх ребер прямокутного паралелепіпеда.
Відповідь: сума довжин усіх ребер прямокутного паралелепіпеда дорівнює 200 см.
Вправа 610° Знайдіть площу поверхні прямокутного паралелепіпеда, виміри якого дорівнюють 9 м, 24 м, 11 м.
(9 м • 24 м) • 2 + (24 м • 11 м) • 2 + (9 м • 11 м) • 2 = 1158 м2
Відповідь: площа поверхні прямокутного паралелепіпеда дорівнює 1158 м2.
Вправа 624 Розв’яжіть рівняння:
|
1) 6х + 8х – 7х = 714 7х = 714 х = 714 : 7 х = (700 + 14) : 7 = 100 + 2 х = 102
|
3) 11х – 6х + 17 = 2042 5х + 17 = 2042 5х = 2042 – 17 5х = 2025 х = 2025 : 5 х = (2000 + 25) : 5 = 400 + 5 х = 405 |