Інші завдання дивись тут ...

© ГДЗ 8next.com, 2013, 2018, 2022

Запитання

Які задачі називають комбінаторними? Задачі, розв’язання яких потребує розгляду та підрахунку всіх можливих випадків, або, як ще прийнято говорити, усіх можливих комбінацій, називають комбінаторними.

 

Розв'язуємо усно

Завдання 1 Одним шаром паперу оклеїли куб, ребро якого дорівнює 3 дм. Скільки квадратних дециметрів паперу витратили на оклеювання куба?

Розв’язання

1) 3 • 3 = 9 (дм²) – площа грані куба.

2) 9 • 6 = 36 (дм²) – площа поверхні куба.

Відповідь: витратили 36 дм² паперу.

 

Завдання 2 Маса 1 л соняшникової олії на 75 г менша від маси 1 л води, а маса 1 л меду на 450 г більша за масу 1 л води. На скільки маса 1 л меду більша за масу 1 л соняшникової олії?

Розв’язання

^{Для води: 1 л = 1 кг = 1000 г}

1) 1000 г – 75 г = 975 (г) – маса 1 л соняшникової олії.

2) 1000 г + 450 г = 1450 (г) – маса 1 л меду.

3) 1450 – 975 = 525 (г) – на стільки більша маса 1 л меду.

Відповідь: на 525 грам.

 

Завдання 3 Скільки центнерів пшениці можна засипати в бункер, який має форму прямокутного паралелепіпеда, якщо його довжина дорівнює 8 м, ширина — 2 м, висота — 1 м, а маса 1 м³ зерна становить 8 ц?

Розв’язання

1) V = 8 м • 2 м • 1 м = 16 м³ – об’єм бункера.

2) 8 • 16 = 128 (ц) – пшениці можна засипати в бункер.

Відповідь: у бункер можна засипати 128 ц пшениці.

 

Завдання 4 Чи встигне Олеся прочитати за 2 год книжку, у якій 65 сторінок, якщо за 6 хв вона може прочитати 3 сторінки?

^{Короткий запис}

^{3 с. — 6 хв}

^{65 с — ? хв}

Розв’язання

^{2 год = 120 хв}

1) 65 : 3 = 2 (хв) – час, за який читає 1 сторінку.

2) 65 : 2 = 32 (ост. 1) – за  стільки хвилин прочитає 65 сторінок.

120 хв > 32 хв

Відповідь: встигне прочитати.

 

Вправи

Вправа 697 Запишіть усі двоцифрові числа, у записі яких використовуються тільки цифри 1 , 2  і 3 (цифри в числі можуть повторюватися). 

Відповідь: 11, 12, 13, 21, 22, 23, 31, 32, 33.

^{Пояснення}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

                    ¹

          ^{1        2       3}

^{Маємо 3 комбінації: 11, 12, 13.}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

                    ²

          ^{1        2       3}

^{Маємо 3 комбінації: 21, 22, 23.}

^{3) Побудуємо схему-дерево для усіх комбінацій з цифрою 3 на першому місці.}

                    ³

          ^{1        2       3}

^{Маємо 3 комбінації: 31, 32, 33.}

^{Усі комбінації: 11, 12, 13, 21, 22, 23, 31, 32, 33.}

  

Вправа 698 Запишіть усі двоцифрові числа, у записі яких використовуються тільки цифри 1 , 2 і 0 (цифри в числі можуть повторюватися). Відповідь: 10, 11, 12, 20, 21, 22.

^{Пояснення.}

^{З цифрою 0 на першому місці не будемо мати трицифрових чисел.}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

                    ¹

           ^{0       1      2}

^{Маємо 3 комбінації: 10, 11, 12.}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

                    ²

           ^{0       1      2}

^{Маємо 3 комбінації: 20, 21, 22.}

^{Усі комбінації: 10, 11, 12, 20, 21, 22.}

 

Вправа 699 Скільки двоцифрових чисел, усі цифри яких різні, можна записати за допомогою цифр 0, 1 і 2? Відповідь: 4 комбінації.

^{пояснення.}

^{З цифрою 0 на першому місці не будемо мати трицифрових чисел.}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

                    ¹

              ^{0           2}

^{Маємо 2 комбінації: 10, 12.}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

                    ²

              ^{0           1}

^{Маємо 2 комбінації: 20, 21.}

^{Разом маємо 4 комбінації (10, 12, 20, 21).}

 

Вправа 700 Скільки двоцифрових чисел, усі цифри яких різні, можна записати за допомогою цифр 1, 2 і 3? Відповідь: 6 комбінацій.

^{Пояснення}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

                    ¹

              ^{2           3}

^{Маємо 2 комбінації: 12, 13.}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

                    ²

              ^{1           3}

^{Маємо 2 комбінації: 21, 23.}

^{3) Побудуємо схему-дерево для усіх комбінацій з цифрою 3 на першому місці.}

                    ³

              ^{1           2}

^{Маємо 2 комбінації: 31, 32.}

^{Разом маємо 6 комбінацій (12, 13, 21, 23, 31, 32).}

 

Вправа 701 Віслюк Іа має три надувні кульки: червону, зелену та жовту. Він хоче подарувати по одній кульці своїм друзям: Вінні-Пуху, П’ятачку і Кролику. Скільки варіантів зробити подарунки своїм друзям є у віслюка Іа?

Розв’язання

Червона	Жовта	Зелена
Іа	П’ятачок	Кролик
Іа	Кролик	П’ятачок
П’ятачок	Іа	Кролик
П’ятачок	Кролик	Іа
Кролик	Іа	П’ятачок
Кролик	П’ятачок	Іа

Відповідь: шість варіантів зробити подарунки своїм друзям є у віслюка Іа.

 

Вправа 702 У футбольному турнірі беруть участь команди 5-А класу, 5-Б класу і 5-В класу. Скільки існує способів розподілу першого і другого місць серед цих команд? Розв’язання якої із задач за номерами 650-653 аналогічне розв’язанню цієї задачі?

Розв’язання

5-А	5-Б	5-В
1 місце	2 місце
1 місце		2 місце
2 місце	1 місце
2 місце		1 місце
	2 місце	1 місце
	1 місце	2 місце

Відповідь: таких варіантів є шість; розв’язання аналогічне 701 задачі.

 

Вправа 703 Запишіть усі трицифрові числа, для запису яких використовуються цифри:

1) 3, 4 і 6 (Цифри в числі не можуть повторюватися.) 

Відповідь: 346, 364, 436, 463, 634, 643

^{Пояснення.}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 3 на першому місці.}

            ³

       ^{4         6}

   ^{6                4}

^{Маємо 2 комбінації: 346, 364}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 4 на першому місці.}

            ⁴

       ^{3        6}

   ^{6                3}

^{Маємо 2 комбінації: 436, 463}

^{3) Побудуємо схему-дерево для усіх комбінацій з цифрою 6 на першому місці.}

            ⁶

       ^{3         4}

   ^{4                 3}

^{Маємо 2 комбінації: 634, 643}

^{Усі комбінації: 346, 364, 436, 463, 634, 643.}

Запишіть усі трицифрові числа, для запису яких використовуються цифри:

2) 4, 7 і 0. (Цифри в числі не можуть повторюватися.) Відповідь: 470, 407, 740, 704.

^{Пояснення.}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 4 на першому місці.}

            ⁴

       ^{7         0}

   ^{0                 7}

^{Маємо 2 комбінації: 470, 407}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 7 на першому місці.}

            ⁷

       ^{4         0}

   ^{0                 4}

^{Маємо 2 комбінації: 740, 704}

^{З цифрою 0 на першому місці не будемо мати трицифрових чисел.}

^{Усі комбінації: 470, 407, 740, 704.}

 

Вправа 704 Скільки різних трицифрових чисел можна записати за допомогою цифр:

1) 1 і 2? (Цифри в числі можуть повторюватися.) 

Відповідь: можна записати 6 трицифрових чисел (112, 122, 121, 212, 211, 221).

^{Пояснення}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

         ¹

     ^{1        2}

 ^{2   1       2    1}

^{Маємо 3 комбінації, щоб наявні були дві цифри одночасно: 112, 122, 121}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

         ²

    ^{1         2}

 ^{2   1       2   1}

^{Маємо 3 комбінації, щоб наявні були дві цифри одночасно: 212, 211, 221}

^{Усіх таких трицифрових чисел шість (112, 122, 121, 212, 211, 221).}

Скільки різних трицифрових чисел можна записати за допомогою цифр:

2) 0 і 1 ? (Цифри в числі можуть повторюватися.) 

Відповідь: можна записати 3 трицифрові числа (110, 101, 100).

^{Пояснення.}

^{З цифрою 0 на першому місці не будемо мати трицифрових чисел.}

^{Побудуємо схему-дерево для усіх комбінацій з цифрою 1 на першому місці.}

         ¹

    ^{1         0}

  ^{0  1       1  0}

^{Маємо 3 комбінації, щоб наявні були дві цифри одночасно (110, 101, 100).} 

 

Вправа 705 Запишіть усі двоцифрові числа, у записі яких використовуються тільки цифри 2, 4, 9 і 0. (Цифри в числі можуть повторюватися.) 

Відповідь: 22, 24, 29, 20, 42, 44, 49, 40, 92, 94, 99, 90.

^{Пояснення}

^{З цифрою 0 на першому місці не будемо мати двоцифрових чисел.}

^{1) Побудуємо схему-дерево для усіх комбінацій з цифрою 2 на першому місці.}

                         ²

          ^{2      4          9      0}

^{Маємо  4 комбінації: 22, 24, 29, 20}

^{2) Побудуємо схему-дерево для усіх комбінацій з цифрою 4 на першому місці.}

                         ⁴

          ^{2      4           9      0}

^{Маємо  4 комбінації: 42, 44, 49, 40}

^{3) Побудуємо схему-дерево для усіх комбінацій з цифрою 9 на першому місці.}

                         ⁹

          ^{2      4           9      0}

^{Маємо  4 комбінації: 92, 94, 99, 90}

^{Усі комбінації: 22, 24, 29, 20, 42, 44, 49, 40, 92, 94, 99, 90.}

 

Вправа 706 Скільки двоцифрових чисел можна записати за допомогою цифр 6, 7, 8 і 9 так, щоб цифри були записані в порядку зростання? 

Відповідь: 6 двоцифрових чисел (67, 68, 60, 78, 79, 89).

^{Пояснення}

^{Цифри у двоцифровому числі не повинні повторюватися.}

^{1) Побудуємо схему-дерево для усіх комбінацій чисел у порядку зростання з цифрою 6 на першому місці.}

          ⁶

 ^{7       8       9}

^{Маємо 3 комбінації двоцифрових чисел: 67, 68, 69}

^{2) Побудуємо схему-дерево для усіх комбінацій чисел у порядку зростання з цифрою 7 на першому місці.}

    ⁷

^{8      9}

^{Маємо 2 комбінації двоцифрових чисел: 78, 79.}

^{3) Побудуємо схему-дерево для усіх комбінацій чисел у порядку зростання з цифрою 8 на першому місці.}

   ⁸

⁹

^{Маємо 1 комбінацію двоцифрових чисел: 89.}

^{4) Нема комбінацій двоцифрових чисел у порядку зростання з цифрою 9 на першому місці.} 

^{Усього 6 таких двоцифрових чисел (67, 68, 69, 78, 79, 89).}

 

Вправа 707 Скільки двоцифрових чисел можна записати за допомогою цифр 6, 7, 8 і 9 так, щоб цифри були записані в порядку спадання? 

Відповідь: 6 таких двоцифрових чисел (98, 97, 96, 87, 86, 76)

^{Пояснення}

^{Цифри у двоцифровому числі не повинні повторюватися.}

^{1) Побудуємо схему-дерево для усіх комбінацій чисел в порядку спадання з цифрою 9 на першому місці.}

             ⁹

^{8            7             6}  

^{Маємо 3 комбінації таких двоцифрових чисел: 98, 97, 96.}

^{2) Побудуємо схему-дерево для усіх комбінацій чисел у порядку спадання з цифрою 8 на першому місці.}

      ⁸

^{7            6} 

^{Маємо 2 комбінації таких двоцифрових чисел: 87, 86.}

^{3) Побудуємо схему-дерево для усіх комбінацій чисел у порядку спадання з цифрою 7 на першому місці.}

   ⁷

⁶

^{Маємо 1 комбінацію таких двоцифрових чисел: 76.}

^{Нема комбінацій двоцифрових чисел у порядку спадання з цифрою 6 на першому місці.}

^{Усього 6 таких двоцифрових чисел (98, 97, 96, 87, 86, 76).}

 

Вправа 708 Скільки існує двоцифрових чисел, сума цифр яких дорівнює 5?

Розв’язання

Цифра	1	2	3	4	5
Цифра	4	3	2	1	0
Число	41	23	32	41	50

Відповідь: 5 двоцифрових чисел (41, 23, 32, 41, 50).

 

Вправа 709 Скільки існує трицифрових чисел, сума цифр яких дорівнює 3?

Розв’язання

Цифра	1	1	1	2	2	3
Цифра	1	0	2	0	1	0
Цифра	1	2	0	1	0	0
Число	111	102	120	201	210	300

Відповідь: 6 трицифрових чисел (111, 102, 120, 201, 210, 300).

 

Вправа 710 Скільки двоцифрових чисел, сума цифр яких дорівнює парному числу, можна скласти з цифр 1, 2, З, 4 (цифри в числі можуть повторюватися)? Відповідь: 8 двоцифрових чисел (11, 13, 22, 24, 31, 33, 42, 44).

^{Пояснення}

^{1) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює парному числу з цифрою 1 на першому місці.}

    ¹

^{1      3}  

^{Маємо 2 комбінації таких двоцифрових чисел: 11, 13.}

^{2) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює парному числу з цифрою 2 на першому місці.}

    ²

^{2      4} 

^{Маємо 2 комбінації таких двоцифрових чисел: 22, 24.}

^{3) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює парному числу з цифрою 3 на першому місці.}

    ³

^{1      3}

^{Маємо 2 комбінації таких двоцифрових чисел: 31, 33.}

^{4) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює парному числу з цифрою 4 на першому місці.}

    ⁴

^{2      4}

^{Маємо 2 комбінації таких двоцифрових чисел: 42, 44.}

^{Усього 8 таких двоцифрових чисел (11, 13, 22, 24, 31, 33, 42, 44).}

 

Вправа 711 Скільки двоцифрових чисел, сума цифр яких дорівнює непарному числу, можна скласти з цифр 0, 1 , 2, З?

Відповідь: 6 двоцифрових чисел (10, 12, 21, 23, 30, 32).

^{Пояснення}

З цифрою 0 на першому місці не будемо мати двоцифрових чисел.

^{1) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює непарному числу з цифрою 1 на першому місці.}

    ¹

^{0      2}  

^{Маємо 2 комбінації таких двоцифрових чисел: 10, 12.}

^{2) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює непарному числу з цифрою 2 на першому місці.}

    ²

^{1      3} 

^{Маємо 2 комбінації таких двоцифрових чисел: 21, 23.}

^{3) Побудуємо схему-дерево для усіх комбінацій чисел сума цифр яких дорівнює непарному числу з цифрою 3 на першому місці.}

    ³

^{0      2}

^{Маємо 2 комбінації таких двоцифрових чисел: 30, 32.}

^{Усього 6 таких двоцифрових чисел (10, 12, 21, 23, 30, 32).}

 

Вправа 712 Василь сканував старі фотографії своєї родини. За кожні наступні 10 хв він сканував більше фотографій, ніж за попередні 10 хв. Разом за 40 хв він відсканував 23 фотографії, причому за останні 10 хв — у 4 рази більше фотографій, ніж за перші 10 хв. Скільки фотографій він відсканував за другі 10 хв?

Розв’язання

х + (х + 4) + (х + 5) + 4х = 23

7х = 23 – 9

7 х = 14

х = 14 : 7

х = 2

2 + 4 = 6 (хв)

Відповідь: 6 хвилин.

 

Вправа 713 На таці лежать 16 фруктів: апельсини, лимони й мандарини. Скільки мандаринів лежить на таці, якщо апельсинів на ній у 5 разів більше, ніж лимонів? 10 мандаринів або 4 мандарини.

 

Вправа 714 Скільки існує різних прямокутників, периметри яких дорівнюють 24 см, а довжини сторін, виражені в сантиметрах, є натуральними числами?

Розв’язання

24 : 2 = 12 (см) – cума двох сторін прямокутника.

1 см х 11 см, 2 см х 10 см, 3 см х 9 см, 4 см х 8 см, 5 см х 7 см, 6 см х 6 см.

 

Вправа 715 Ганнуся має З0 однакових кубиків. Скільки різних прямокутних паралелепіпедів вона може з них скласти, якщо для побудови одного паралелепіпеда треба використати всі наявні З0 кубиків?

Розв’язання

V = abc

1) 30 = 1 • 1 • 30 2) 30 = 1 • 2 • 15 3) 30 = 1 • 3 • 10

3) 30 = 1 • 6 • 5 4) 30 = 2 • 3 • 5

Відповідь: можна скласти 5 прямокутних паралелепіпедів розмірами:

1 х 1 х 30, 1 х 2 х 15, 1 х 3 х 10, 1 х 6 х 5, 2 х 3 х 5. 

 

Вправа 716 На прямій позначили чотири точки: А, В, С і D. Скільки існує відрізків з кінцями в позначених точках?

А_____B______C_______D

Відповідь: існує 6 відрізків (АВ, АС, АD, ВС, ВD, СD).

 

Вправа 717 Підніжжя гори та її вершину зв’язують три стежки. Скільки існує маршрутів, як і ведуть від підніжжя до вершини й потім униз до підніжжя?

Розв’язання

Розв’язання

^{Позначимо вершину гори: С1}

^{Позначимо підняжжя гори: С2, С3. С4.}

              С1

 

    С2      С3      С4

С2С1С2,  С2С1С3,  С1С2С4

С3С1С2,  С3С1С3,  С3С1С4

С4С1С2,  С4С1С3,  С4С1С4

Відповідь: 9 маршрутів.

 

Вправа 718 Тетянка має чотири плаття та дві пари туфель. Скільки у Тетянки є варіантів вибрати наряд?

Розв’язання

^{Позначимо плаття: п1, п2, п3, п4}

^{Позначимо туфлі: т1, т2.}

п1т1, п1т2

п2т1, п2т2

п3т1, п3т2

п4т1, п4т2

Відповідь: 8 варіантів нарядів.

 

Вправа 719 У загоні космонавтів є три пілоти та два інженери. Скільки існує способів скласти екіпаж з одного пілота й одного інженера?

Розв’язання

^{Позначимо пілотів: п1, п2, п3.}

^{Позначимо інженерів: і1, і2.}

п1і1, п1і2

п2і1, п2і2

п3і1, п3і2

Відповідь: 6 екіпажів.

 

Вправа 720 На рисунку 194 зображено план одного району міста. Відрізками зображено вулиці. Скільки існує маршрутів з точки А в точку В , якщо пересуватися дозволено вулицями, що ведуть на північ або на схід?

Розв’язання

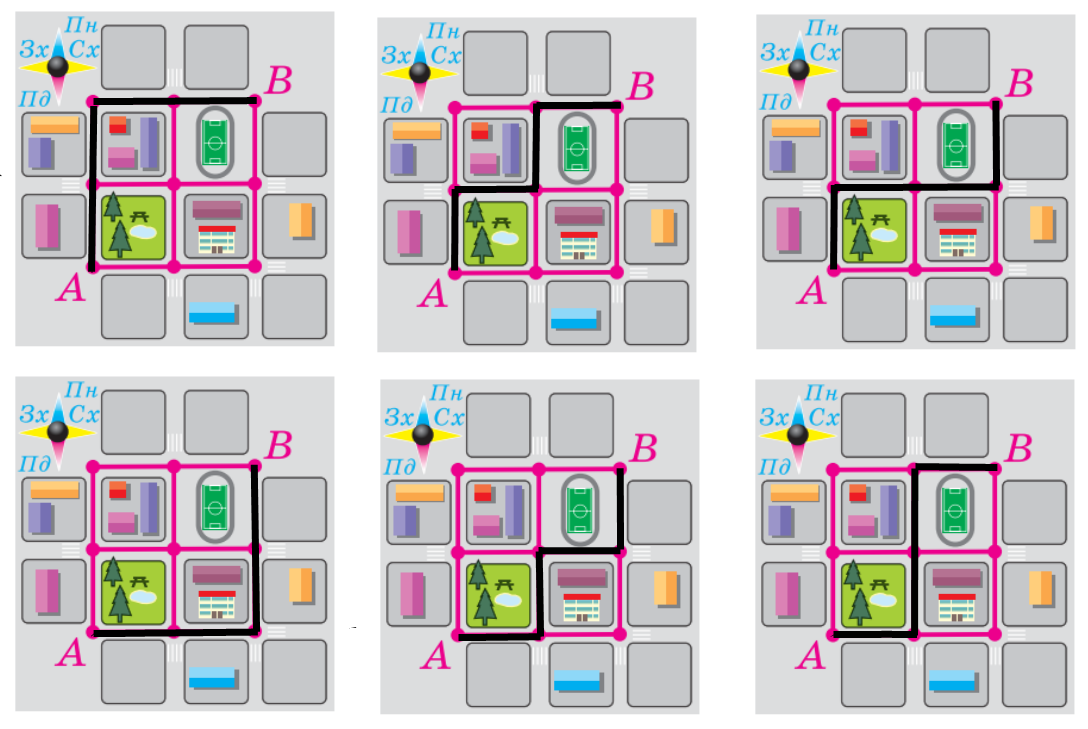
Відповідь: існує 6 маршрутів.

 

Вправи для повторення

Вправа 721 Розв’яжіть рівняння

1) 1376 : (34 – х) = 86 34 – х = 1376 : 86 34 – х = 16 х = 34 – 16 х = 18	2) 9680 : (х + 219) = 16 х + 219 = 9680 : 16 х + 219 = 605 х = 605 – 219 х = 386
3) (х – 57) : 29 = 205 х – 57 = 205 • 29 х – 57 = 5945 х = 5945 + 57 х = 6002	4) (х – 72) • 9 = 927 х – 72 = 927 : 9 х – 72 = (900 + 27) : 9 х – 72 = 103 х = 103 + 72 х = 175

Вправа 722 Один із доданків у 14 разів більший за другий. У скільки разів їх сума більша за менший із доданків?

Розв’язання

Нехай х – менший доданок, тоді 14х – більший доданок,

14х + х = 15х – сума.

15х : х = 15 (разів) – у стільки разів сума більша від меншого доданку.

Відповідь: сума у 15 разів більша від меншого доданку.

 

Вправа 723 Від’ємник у 12 разів більший за різницю. У скільки разів зменшуване більше за різницю?

Розв’язання

Нехай х – різниця, тоді 12х – від’ємник,

12х + х = 13х – зменшуване.

13х : х = 13 (разів) – у стільки разів зменшуване більше за різницю.

Відповідь: зменшуване у 13 разів більше за різницю.

 

Вправа 724 Розгадайте кросворд: 

По горизонталі: 

1. Результат дії ділення (частка). 

2. Одиниця часу (секунда). 

3. Одиниця виміру кутів (градус).  

4. Компонент множення (множник). 

5. Компонент додавання (доданок).

По вертикалі: 6. Цариця наук (математика).

 

Задача від Мудрої Сови

Задача 725 У класі З0 учнів. Вони сидять по двоє за 15 партами так, що половина всіх дівчинок сидить з хлопчиками. Чи можна учнів класу пересадити так, щоб половина всіх хлопчиків сиділа з дівчинками?

Розв’язання

Оскільки половина дівчаток сидить з хлопчиками, значить кількість дівчаток виражається парним числом.

Інша половина дівчаток утворюють пару дівчинка-дівчинка, значить половина дівчаток теж виражається парним числом. 

Кількість дівчаток ділиться на 4. Щоб половина хлопчиків сиділа з дівчатками, кількість хлопців теж повинна ділитися на 4. Тоді кількість учнів має ділитися на 4. Оскільки кількість усіх дітей, виражена числом 30, не ділиться на 4 без остачі, отже, дітей пересадити так неможливо.

 

------------------------- у підручнику за 2013 рік ----------------------

Вправа 667** Кіт Базиліо та лисиця Аліса вирішили вкрасти золотий ключик, який зберігається в комірці тата Карла. Щоб туди потрапити, слід підібрати двоцифровий код. Їм відомо, що двері в комірку зачиняє Буратіно, який знає поки що тільки чотири цифри: 0, 1, 2 і 3. Яку найбільшу кількість варіантів доведеться перебрати коту й лисиці, щоб відчинити двері?

Розв’язання

00, 01, 02, 03, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33.

Відповідь: 16 варіантів.

 

Вправа 671” Команді пропонують футболки трьох кольорів: червоного, зеленого та синього, і шорти двох кольорів — білого та жовтого. Скільки варіантів вибрати форму є у команди?

Розв’язання

Позначимо футболки: ч, з, с.

Позначимо шорти: б, ж.

чб, чж

зб, зж

сб, сж

Відповідь: 6 варіантів форми.

 

Вправа 674” У записі 1 * 2 * 3 * 4 замість кожної зірочки можна поставити знак ≪+≫ або знак ≪•≫. Чому дорівнює найбільше значення виразу, який можна отримати?

Розв’язання

+	+	+
+	+	•
+	•	•
•	•	•
•	+	+
•	•	+
•	+	•
+	•	+

1 + 2 + 3 + 4 = 10

1 + 2 + 3 • 4 = 15

1 + 2 • 3 • 4 = 25

1 • 2 • 3 • 4 = 24

1 • 2 + 3 + 4 = 9

1 • 2 • 3 + 4 = 10

1 • 2 + 3 • 4 = 14

1 + 2 • 3 + 4 = 11

Відповідь: найбільше значення - 25.

 

Розв'язуємо усно

Завдання 2 Об’єм прямокутного паралелепіпеда дорівнює 240 см³. Якою з даних трійок чисел можна задати виміри цього паралелепіпеда:

1) 4 см, 6 см, 12 см;          3) 3 см, 5 см, 10 см;

2) 5 см, 6 см, 8 см;            4) 10 см, 10 см, 24 см?

Розв’язання

1) 240 : 4 : 6 ≠ 12

2) 240 : 5 : 6 = 8

Відповідь: 5 см, 6 см, 8 см - виміри паралелепіпеда об’ємом 240 см³. 

 

Завдання 4 Що більше і на скільки:

1) квадрат суми чисел 4 і 3 чи сума їх квадратів;

2) різниця квадратів чисел 10 і 8 чи квадрат їх різниці;

3) різниця кубів чисел 5 і 3 чи куб їх різниці?

Розв’язання

1) (4 + 3)² > 4² + 3²,  бо (4 + 3)² = 7² = 49, 4² + 3² = 16 + 9 = 25, а 49 > 25

2) 10² – 8² > (10 – 8)²,  бо 10² – 8² = 100 – 64 = 36, (10 – 8)² = 2² = 4, а 36 > 4 

3) 5³ – 3³ > (5 – 3)³, бо 5³ – 3³ = 125 – 27 = 98, (5 – 3)³ = 2³ = 8, а 98 > 8 

 

Вправа 674 Відстань між двома селами дорівнює 28 км. Із цих сіл одночасно в одному напрямку виїхали мотоцикліст і автобус. Автобус їхав попереду зі швидкістю 42 км/год, а мотоцикліст їхав зі швидкістю 56 км/год. Через скільки годин після початку руху мотоцикліст наздогнав автобус?

Розв’язання

          56 км/год                42 км/год

------------------------------> ------------------->

             28 км

1) 56 – 42 = 14 (км/год) – швидкість зближення.

2) 28 : 14 = 2 (год) – час зустрічі.

Відповідь: мотоцикліст наздогнав автобус через 2 год після початку руху.

Інші завдання дивись тут ...