Нагадаємо, що точка і пряма можуть мати одну спільну точку, дві точки, або жодної.
Дотична до кола — пряма, яка має з колом лише одну спільну точку, яку називають точкою дотику.
Пряма а – дотична до кола, K – точка дотику.
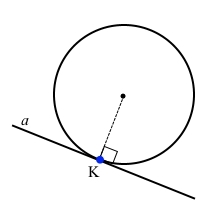
◊ Теорема про властивість дотичної.
Дотична до кола є перпендикулярна до радіуса, який проведений в точку дотику.
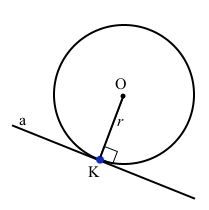
Якщо a – дотична до кола з центром О в точці К, відрізок ОК – радіус кола,
тоді а ﬩ ОК (a ﬩ r).
◊ Теорема (обернена до теореми про властивість дотичної).
Якщо пряма проходить через кінець радіуса кола і перпендикулярна до цього радіуса, то ця пряма є дотичного до цього кола.

Якщо ОК – радіус кола з центром в точці О, причому пряма а ﬩ ОК,
тоді а – дотична до цього кола в точці К.
Наслідок. Відстань від центра кола до дотичної цього кола дорівнює радіусу кола.
Через одну точку М поза колом можна провести тільки дві дотичні.
Частини дотичних від спільної точки поза колом і точками дотику називають відрізками дотичних, проведених з точки М.
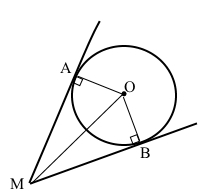
МА і МВ – відрізки дотичних.
◊ Теорема про властивість відрізків дотичних, проведених з однієї точки.
Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
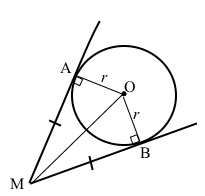
Маємо коло з центром О. МА і МВ – дотичні прямі до цього кола, проведені з точки М. У точках дотику А і В виконується МА ﬩ ОА і МВ ﬩ ОВ, де ОА = ОВ – радіуси кола.
Тоді відрізки МА = МВ.