© Барна Р., 2019
Серія "Вчимось разом" до підручника "Математика 2 клас Будна Н., Беденко М."
Завдання 1031
|
1) Зменшили на 19 числа (відняли число 19): |
2) Збільшили на 47 числа (додали число 47): |
|
25 – 19 = 25 – 20 + 1 = 5 + 1 = 6 57 – 19 = 57 – 20 + 1 = 37 + 1 = 36 81 – 19 = 81 – 11 – 8 = 70 – 8 = 62 99 – 19 = 80 |
12 + 47 = 59 49 + 47 = 80 + 16 = 96 47 + 47 = 80 + 14 = 94 53 + 47 = 90 + 10 = 100 |
Завдання 1032 Складена задача на знаходження суми добутків
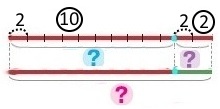
На хокейному майданчику 10 польових гравців і 2 воротарі. Скільки рукавиць у всіх хокеїстів?
|
Короткий запис У польових гравців — ? р., 10 гравців по 2 рукавиці У воротарів — ? р., 2 воротарі по 2 рукавиці Всього — ? Схема
Вираз 2 • 10 + 2 • 2 План розв’язування 1) Скільки рукавиць у польових гравців? 2) Скільки рукавиць у воротарів? 3) Скільки рукавиць у всіх хокеїстів? Розв’язання 1) 2 • 10 = 20 (р.) – рукавиць у польових гравців. 2) 2 • 2 = 4 (р.) – рукавиць у воротарів. 3) 20 + 4 = 24 (р.) – всього рукавиць у всіх хокеїстів. |
2 спосіб Оскільки у всіх гравців однакова кількість рукавиць, тому Короткий запис Рукавиці — ? р., ? (10 гравців і 2 воротарі) по 2 рукавиці Схема
Вираз 2 • (10 + 2) План розв’язування 1) Скільки всього хокеїстів? 2) Скільки рукавиць у всіх хокеїстів? Розв’язання 1) 10 + 2 = 12 (х.) – всього хокеїстів. 2) 2 • 12 = 12 • 2 = 12 + 12 = 24 (р.) – рукавиць у всіх хокеїстів. |
Відповідь: у всіх хокеїстів 24 рукавиці.
Завдання 1033 Знайшли значення виразу
Якщо а = 0, тоді а : 6 + 25 = 0 : 6 + 25 = 0 + 25 = 25
Якщо а = 6, тоді а : 6 + 25 = 6 : 6 + 25 = 1 + 25 = 26
Якщо а = 12, тоді а : 6 + 25 = 12 : 6 + 25 = 2 + 25 = 27
Якщо а = 42, тоді а : 6 + 25 = 42 : 6 + 25 = 7 + 25 = 25 + 5 + 2 = 32
Завдання 1034 Складена задача на різницеве порівняння суми і числа
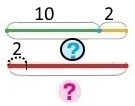
Від хати до школи є дві дороги. На скільки метрів пряма дорога коротша (менше метрів)?
Короткий запис
Пряма дорога — 52 м; на ? м менше
Непряма дорога — ?, 19 м і 56 м
Вираз (19 + 56) – 52
Розв’язання
1) 19 + 56 = 56 + 4 + 15 = 75 (м) – довжина непрямої дороги.
2) 75 – 52 = 23 (м) – на стільки пряма дорога коротша.
Відповідь: на 23 метри пряма дорога коротша.
Завдання 1035 Порядок дій
|
54 : 6 + 7 • 3 = 9 + 21 = 30 1) 54 : 6 = 9 2) 7 • 3 = 21 3) 9 + 21 = 20 + 10 = 30 |
28 : 7 + (32 – 28) • 7 = 4 + 4 • 7 = 32 1) 32 – 28 = 32 – 30 + 2 = 4 2) 4 • 7 = 28 3) 28 : 7 = 4 4) 4 + 28 = 28 + 2 + 2 = 32 |
Завдання 1036 Кожну сторону шестикутника збільшили на 2 см. Чи можна дізнатися, на скільки сантиметрів збільшився його периметр?
Міркуємо так. Якщо кожну сторону шестикутника збільшити на 2 см, тоді периметр збільшиться на
2 см • 6 = 12 см
Відповідь: периметр збільшився на 12 сантиметрів.
Завдання 1037
З аркуша паперу, не розрізаючи його, можна зробити макет циліндра, конуса.
Завдання 1038 Доба
|
Годинник |
|
|
|
|
|
Час |
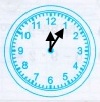
від полудня до опівночі 23 год 10 хв |
від опівночі до полудня 0 год 05 хв |
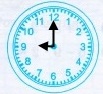
від полудня до опівночі 21 год |
від опівночі до полудня 3 год 30 хв |
|
Час між показами |
24 год – 23 год 10 хв + 0 год 5 хв = 50 хв + 0 год 5 хв = 55 хв |
24 год – 21 год + 3 год 30 хв = 3 год + 3 год 30 хв = 6 год 30 хв |
||
Завдання 1039 Складена задача на віднімання добутку від числа
Семеро гномів знайшли 60 полуничок. Скільки полуничок вони донесли додому, якщо по дорозі кожен гном з'їв по 5 ягід?
|
Було |
З’їли |
Залишилось |
|
60 полуничок |
7 гномів по 5 полуничок |
? |
Короткий запис
Було (знайшли) — 60 полуничок
З’Їли — ? п., 7 гномів по 5 полуничок
Залишилось — ?
Схема
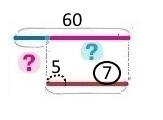
Вираз 60 – 5 • 7
|
Короткий запис №1 З’Їли — ? п., 7 гномів по 5 полуничок |
Короткий запис №2 Було (знайшли) — 60 полуничок З’Їли — 35 полуничок Залишилось — ? |
План розв’язування
1) Скільки полуничок вони з’їли по дорозі?
2) Скільки полуничок вони донесли додому?
Розв’язання
1) 5 • 7 = 35 (п.) – полуничок вони з’їли по дорозі.
2) 60 – 35 = 60 – 40 + 5 = 25 (п.) – полуничок вони донесли додому.
Відповідь: додому вони донесли 25 полуничок.
Завдання 1040 Ділення на число 5
|
а |
20 |
30 |
15 |
45 |
25 |
35 |
10 |
40 |
|
а : 5 |
4 |
6 |
3 |
9 |
5 |
7 |
2 |
8 |
Завдання 1041
Перший день у 2019 році (1 січня) припадає на день тижня – вівторок.
Останній день у 2019 році (31 грудня) припадає на день тижня – вівторок.
Завдання 1042
У році 12 місяців. Найкоротший з них — лютий. Останній день лютого у 2019 році (28 люте) припадає на день тижня – четвер.
Завдання 1043 Днів у кожному місяці
Найдовші місяці в році (мають 31 день): січень, березень, травень, липень, серпень, жовтень, грудень.
Завдання 1044
|
35 : 5 • 2 = 7 • 2 = 14 24 : 4 • 3 = 6 • 3 = 18 45 : 5 • 6 = 9 • 6 = 54 28 : 4 • 5 = 7 • 5 = 35 |
30 : 5 • 8 = 6 • 8 = 48 15 : 5 • 4 = 3 • 4 = 12 16 : 4 • 5 = 4 • 5 = 20 18 : 3 • 2 = 6 • 2 = 12 |
Завдання 1045 Складена задача на знаходження невідомого доданку
У театрі працюють 36 артистів. Четверта частина з них співає, а решта — танцюють. Скільки танцюристів працює в театрі?
|
Співає |
Танцюють |
Всього |
|
1/4 всього |
? |
36 артистів |
Короткий запис
Співає — ?, 1/4 від всього артистів
Танцює — ?
Всього — 36 артистів
Схема
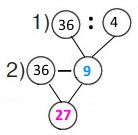
Вираз 36 – 36 : 4
|
Короткий запис №1 Співає — ?, 1/4 від всього артистів Всього — 36 артистів
|
Короткий запис №2 Співає — 9 артистів Танцює — ? Всього — 36 артистів |
План розв’язування
1) Скільки співаків працює в театрі?
2) Скільки танцюристів працює в театрі?
Розв’язання
1) 36 : 4 = 9 (сп.) – співаків працює в театрі.
2) 36 – 9 = 36 – 6 – 3 = 27 (т.) – танцюристів працює в театрі.
2 спосіб (для старших класів)
1) Якщо 1/4 всіх – це співаки, тоді залишилося 3/4 – це танцюристи, тому
36 : 4 • 3 = 27 (т.) – танцюристів працює в театрі.
Відповідь: у театрі працює 27 танцюристів.
Завдання 1046
|
Добуток чисел 4 і 6: 4 • 6 = 24 |
Різниця чисел 21 і 3: 21 – 3 = 18 |
Частка чисел 21 і 3: 21 : 3 = 7 |
Сума чисел 4 і 6: 4 + 6 = 10 |
Завдання 1047 За день у кафе приготували 23 порції шоколадного морозива, полуничного — на 7 порцій менше, ніж шоколадного, а бананового — на 3 порції менше, ніж полуничного. Скільки порцій бананового морозива приготували в кафе?
23 – 7 – 3 = 13 (п.)
Відповідь: приготували 13 порцій бананового морозива.
Завдання 1048
Якщо а = 0, тоді 58 – 5 • а = 58 – 5 • 0 = 58 – 0 = 58
Якщо а = 1, тоді 58 – 5 • а = 58 – 5 • 1 = 58 – 5 = 53
Якщо а = 2, тоді 58 – 5 • а = 58 – 5 • 2 = 58 – 10 = 48
Якщо а = 5, тоді 58 – 5 • а = 58 – 5 • 5 = 58 – 25 = 33
Якщо а = 10, тоді 58 – 5 • а = 58 – 5 • 10 = 58 – 50 = 8
Завдання 1049
Зима (січень, лютий, грудень), весна (березень, квітень, травень), літо (червень, липень, серпень), осінь (вересень, жовтень, листопад).
Завдання 1050
|
Короткий запис Червень — 30 днів Липень — 31 день Серпень — 31 день Всього — ? |
30 + 31 + 31 = 90 + 2 = 92 (дн.) – літніх днів у році. |
Завдання 1051
Повних тижнів (7 днів) у травні 2019 року: 3 тижні.
Неповних тижнів у травні 2019 року: 2 тижні.
Завдання 1052 Літак коштує стільки, скільки автобус і машинка разом. Яка іграшка дорожча: літак чи автобус?
Міркуємо так. А + М = Л, сума більша, ніж доданок, тому Л > А
Відповідь: літак дорожчий, ніж автобус.
Завдання 1053
|
24 : 4 + 63 = 6 + 63 = 69 78 – 18 : 2 = 78 – 9 = 78 – 8 – 1 = 69 4 • 6 + 24 = 24 + 24 = 48 3 • 7 + 29 = 21 + 29 = 40 + 10 = 50 |
54 – 40 : 5 = 54 – 8 = 54 – 4 – 4 = 46 18 : 3 + 46 = 6 + 46 = 46 + 4 + 2 = 52 5 • 6 + 28 = 30 + 28 = 58 32 – 3 • 9 = 32 – 27 = 32 – 30 + 3 = 5 |
Завдання 1054
Циліндри схожі на труби, бочку, склянку, криничні кільця.
Завдання 1055 Складена задача на збільшення на деяке число (у непрямій формі)
Леопард може стрибнути на 7 м, що на 1 м далі (більше метрів), ніж собака. Знайди довжину стрибка антилопи, якщо вона може стрибнути на 4 м далі від собаки.
Короткий запис
Леопард — 7 м, це на 1 м більше, ніж собака
Собака — ?
Антилопа — ?, на 4 м більше, ніж собака
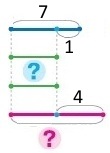
Вираз (7 – 1) + 4
|
Короткий запис №1 Леопард — 7 м, це на 1 м більше Собака — ? |
Короткий запис №2 Собака — 6 м Антилопа — ?, на 4 м більше |
План розв’язування
1) Яка довжина стрибка собаки?
2) Яка довжина стрибка антилопи?
Розв’язання
Якщо стрибок леопарда на 1 м більший за стрибок собаки, це означає, що стрибок собаки на 1 м менший, тому
1) 7 – 1 = 6 (м) – довжина стрибка собаки.
2) 6 + 4 = 10 (м) – довжина стрибка антилопи.
Відповідь: довжина стрибка антилопи 10 метрів.
Завдання 1056
а) Відстань між опорами моста менша, ніж 12 м. (Так, бо 16 м – 7 м = 9 м)
б) Відстань між опорами моста більша, ніж 20 м (Ні)
в) Відстань між опорами моста більша, ніж 12 м, але менша, ніж 20 м (Ні).
Додаткові завдання
Завдання 1
Міркуємо так. Перестрибуючи з купини на купину, чоловічки набирають стільки балів, скільки вказано між купинами. За один стрибок червоний набере 2 бали, зелений – 4 бали, синій – 7 балів. Найбільшу кількість балів набере синій чоловічок.
Відповідь: синій чоловічок.
Завдання 2
Міркуємо так. Перестрибуючи з купини на купину, чоловічки набирають стільки балів, скільки вказано між купинами. За один стрибок червоний – 5 балів, зелений – 6 балів, синій – 4 бали. Найбільшу кількість балів набере зелений чоловічок.
Відповідь: зелений чоловічок.
Завдання 3
Міркуємо так. За 1 стрибок синій чоловічок набере 10 балів. Щоб набрати стільки ж балів, червоний чоловічок має зробити 4 стрибки (стільки стрибків, скільки доданків у виразі 1 + 2 + 2 + 4).
Відповідь: 4 стрибки.
Завдання 4
Міркуємо так. Відомо, що лише один чоловічок, зробивши кілька стрибків, може набрати в сумі 100 балів. Червоний може набрати 10 + 80 = 90 або 10 + 80 + 20 = 110. Зелений може набрати 20 + 80 = 100. Синій може набрати 90 або 90 + 40 = 130. У сумі сто балів набере зелений чоловічок.
Відповідь: зелений чоловічок.
Завдання 5
Міркуємо так. Відомо, якщо чоловічки роблять по два стрибки, то бали додаються. За два стрибки червоний чоловічок набере балів 5 + 1 = 6, зелений – 9 + 1 = 10, синій – 3 + 4 = 7. За два стрибки найбільшу кількість балів набере зелений чоловічок.
Відповідь: зелений чоловічок.
Завдання 6
Міркуємо так. Відомо, що обидва чоловічки хочуть набрати однакову кількість балів. Якщо маємо числа 2 і 5, тоді за переставним законом множення 2 • 5 = 5 • 2 = 10, тому червоний повинен зробити 5 стрибків по 2 бали, а синій 2 стрибки по 5 балів.
Відповідь: червоний 5 стрибків, зелений – 2 стрибки.
Завдання 7
Міркуємо так. Синя указка спрямована горизонтально, тобто на зелене сонечко.
Відповідь: на зелене сонечко.
Завдання 8
На блакитне сонечко не спрямована жодна указка.
Завдання 9
Промені блакитної і жовтої указок перетнуться.
Завдання 10
По горизонтальних прутах переміщаються синій і жовтий чоловічки.
По вертикальних прутах переміщаються зелений і червоний чоловічки.
Завдання 11
Міркуємо так. Горизонтально переміщається фіолетовий чоловічок. Вертикально переміщається зелений чоловічок. По похилих прутах пересуваються червоний і блакитний чоловічки.
Відповідь: червоний і блакитний чоловічки.
Завдання 12
Міркуємо так. Вертикальні прути куба пофарбували червоним кольором, їх 4 сторони. Горизонтальних синіх – 8 сторін. 8 > 4, тому більше горизонтальних прутів.
Відповідь: горизонтальних прутів.
Завдання 13
Міркуємо так. Якщо буря повалила будинок на бік, і підлоги та стелі в ньому стали вертикальними, тоді всі стіни будуть горизонтальними.
Відповідь: так.
Завдання 14
Міркуємо так. Якщо всередині конструкції, що має форму куба, звели вертикальну стінку, тоді справа від стінки фіолетовий і коричневий чоловічки, а зліва – зелений і червоний.
Відповідь: справа – фіолетовий і коричневий, зліва – зелений і червоний.
Завдання 15
Міркуємо так. Якщо в мішень двічі вистрелили кульками з фарбою (позначки на 20 і 30). Щоб в сумі набрати 100 балів, тоді треба влучити у 50, бо 20 + 30 + 50 = 100.
Відповідь: 50.
Завдання 16
Міркуємо так. Якщо у мішень мають намір вистрелити двічі, щоб при цьому набрати 100 балів, тоді треба двічі попасти у число 50, бо 50 + 50 = 100.
Відповідь: так.
Завдання 17
Міркуємо так. Відомо, що двоє стрільців зробили по два постріли. Перший набрав 20 + 30 = 50 балів синіми кульками, другий набрав 40 + 10 = 50 балів червоними кульками. Обидва стрільці набрали однакову кількість балів, тому ніхто з них не набрав більше балів.
Відповідь: ніхто.
Завдання 18
Міркуємо так. Відомо, що кожен з двох стрільців вистрелив по мішені однією синьою і однією червоною кульками. Сині кульки мають бали 20 і 30, а червоні – 40 і 10. Тоді маємо такі комбінації вистрілів: 20 + 40 = 60, 20 + 10 = 30, 30 + 40 = 70, 30 + 10 = 40. Також відомо, що перший стрілець набрав в сумі на 20 балів більше, ніж другий, тому перший влучив у 20 і 40, а другий – у 30 і 10.
Відповідь: перший – 20 і 40, другий – 30 і 10.
Завдання 19
Міркуємо так. Відомо, що один стрілець стріляв червоними кульками з балами 5 + 1 = 6, другий — синіми з балами 4 + 4 = 8 , а третій — зеленими з балами 2 + 3 = 5. Найбільше балів набрав стрілець зі синіми кульками.
Відповідь: синіми кульками.
Завдання 20
Міркуємо так. Відомо, що двоє стрільців зробили по три постріли кульками різних кольорів. Також бали за кольорами кульок: зелені – 2 і 3, сині – 4 і 4, червоні – 5 і 1. Якщо другий вибив 7 балів, то його постріли 2 + 4 + 1 = 7. Отже, перший стрілець набрав 3 + 4 + 5 = 12 балів.
Відповідь: 12 балів.
Завдання 21
Міркуємо так. Відомо, що у мішень із балами від 1 до 5 стрілець має намір вистрелити п'ятьма рожевими кульками. Щонайбільше він може набрати 5 • 5 = 25 балів, тому він не зможе набрати 30 балів.
Відповідь: не зможе.