![]()
Серія "Вчимось разом" до підручника
"Математика 2 клас Скворцова С.О., Онопрієнко О.В.", 2019 року видання
СТОРІНКА 130
Завдання 1
1) Проста задача на збільшення у декілька разів
Вітя зловив 5 окунів, а тато — у 4 рази більше. Скільки окунів зловив тато?
Короткий запис
Вітя — 5 окунів
Тато — ?, у 4 рази більше
Схема
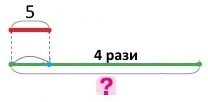
Розв’язання
5 • 4 = 20 (ок.) – окунів зловив тато
Відповідь: тато зловив 20 окунів
2) Складена задача
Вітя зловив 5 окунів, а тато — у 4 рази більше. Скільки окунів зловили Вітя і тато разом?
|
Вітя |
Тато |
Всього |
|
5 окунів |
у 4 рази більше |
? |
Короткий запис
Вітя — 5 окунів
Тато — ?, у 4 рази більше
Всього — ?
Схема
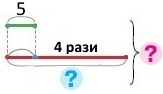
Вираз 5 + 5 • 4
|
Короткий запис №1 Вітя — 5 окунів Тато — ?, у 4 рази більше |
Короткий запис №2 Вітя — 5 окунів Тато — 20 окунів Всього — ? |
План розв’язування
1) Скільки окунів зловив тато?
2) Скільки окунів зловили Вітя і тато разом?
Розв’язання
1) 5 • 4 = 20 (ок.) – окунів зловив тато
2) 5 + 20 = 25 (ок.) – окунів зловили Вітя і тато разом
2 спосіб
Міркуємо так
Якщо зловив 5 окунів, а тато — у 4 рази більше, це також означає, у Віті одна частина окунів, а в тата 4 таких частини, тоді разом 5 частин по 5 окунів
5 • 5 = 25 (ок.) – окунів зловили Вітя і тато разом
Відповідь: Вітя і тато разом зловили 25 окунів
3) Вітя зловив 5 окунів, а тато — у 4 рази більше. На скільки більше окунів зловив тато, ніж Вітя?
Короткий запис
Вітя — 5 окунів
Тато — ?, у 4 рази більше; на ? більше
Схема
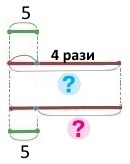
Вираз 5 • 4 – 5
|
Короткий запис №1 Вітя — 5 окунів Тато — ?, у 4 рази більше |
Короткий запис №2 Вітя — 5 окунів Тато — 20 окунів, на ? більше |
План розв’язування
1) Скільки окунів зловив тато?
2) На скільки більше окунів зловив тато, ніж Вітя?
Розв’язання
1) 5 • 4 = 20 (ок.) – окунів зловив тато
2) 20 – 5 = 15 (ок.) – на стільки більше окунів зловив тато, ніж Вітя
Відповідь: тато зловив на 15 окунів більше, ніж Вітя
Завдання 2
1) Вітя зловив 5 окунів, а тато — у 4 рази більше. Дідусь зловив у 2 рази менше окунів, ніж тато. Скільки окунів зловив дідусь?
Короткий запис
Вітя — 5 окунів
Тато — ?, у 4 рази більше, ніж Вітя
Дідусь — ?, у 2 рази менше, ніж тато
Схема
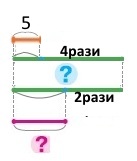
Вираз 5 • 4 : 2
|
Короткий запис №1 Вітя — 5 окунів Тато — ?, у 4 рази більше |
Короткий запис №2 Тато — 20 окунів Дідусь — ?, у 2 рази менше |
План розв’язування
1) Скільки окунів зловив тато?
2) Скільки окунів зловив дідусь?
Розв’язання
1) 5 • 4 = 20 (ок.) – окунів зловив тато
2) 20 : 2 = 10 (ок.) – окунів зловив дідусь
Відповідь: дідусь зловив 10 окунів
2) Вітя зловив 5 окунів, а тато — у 4 рази більше. Дідусь зловив у 2 рази менше окунів, ніж тато. Скільки окунів зловили Вітя, його тато і дідусь разом?
Короткий запис
Вітя — 5 окунів
Тато — ?, у 4 рази більше, ніж Вітя
Дідусь — ?, у 2 рази менше, ніж тато
Всього — ?
Схема
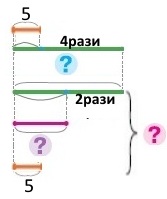
Вираз 5 + 5 • 4 + 5 • 4 : 2
|
Короткий запис №1 Вітя — 5 окунів Тато — ?, у 4 рази більше |
Короткий запис №2 Тато — 20 окунів Дідусь — ?, у 2 рази менше
|
Короткий запис №2 Вітя — 5 окунів Тато — 20 окунів Дідусь — 10 окунів Всього — ? |
План розв’язування
1) Скільки окунів зловив тато?
2) Скільки окунів зловив дідусь?
3) Скільки окунів зловили Вітя, його тато і дідусь разом?
Розв’язання
1) 5 • 4 = 20 (ок.) – окунів зловив тато
2) 20 : 2 = 10 (ок.) – окунів зловив дідусь
3) 5 + 20 + 10 = 35 (ок.) – окунів зловили Вітя, його тато і дідусь разом
Відповідь: Вітя, його тато і дідусь зловили 35 окунів
СТОРІНКА 131
Завдання 2
|
Різницю між числами знаходимо дією віднімання: |
|
|
Жовті — 3 круги Червоні — 6 кругів, на ? більше 6 – 3 = 3 (к.) |
Жовті — 3 круги, на ? менше Червоні — 6 кругів 6 – 3 = 3 (к.) |
|
Скільки разів у 6 вміщується по 3 — знаходимо дією ділення: |
|
|
Жовті — 3 круги Червоні — 6 кругів, у ? разів більше 6 : 3 = 2 (рази) |
Жовті — 3 круги, у ? разів менше Червоні — 6 кругів 6 : 3 = 2 (рази) |
Завдання 3 Порівняння чисел
На скільки одне число більше або менше за інше?
3 < 15 на 12 (15 – 3 = 12) 32 > 4 на 28 (32 – 4 = 32 – 2 – 2 = 28)
3 < 27 на 24 (27 – 3 = 24) 30 > 5 на 25 (30 – 5 = 25)
8 < 24 на 16 (24 – 8 = 24 – 4 – 4 = 16) 45 > 5 на 40 (45 – 5 = 40)
16 > 2 на 14 (16 – 2 = 14) 3 < 21 на 18 (21 – 3 = 21 – 1 – 2 = 18)
2 < 12 на 10 (12 – 2 = 10) 35 > 5 на 30 (35 – 5 = 30)
У скільки разів більше або менше?
3 < 15 у 5 разів (15 : 3 = 5) 32 > 4 у 8 разів (32 : 4 = 8)
3 < 27 у 9 разів (27 : 3 = 9) 30 > 5 у 6 разів (30 : 5 = 6)
8 < 24 у 3 рази (24 : 8 = 3) 45 > 5 у 9 разів (45 : 5 = 9)
16 > 2 у 8 разів (16 : 2 = 8) 3 < 21 у 7 разів (21 : 3 = 7)
2 < 12 у 6 разів (12 : 2 = 6) 35 > 5 у 7 разів (35 : 5 = 7)
Завдання 4 Складені задачі з непов’язаними між собою запитаннями
1) Довжина килимової доріжки 8 м, а ширина — 2 м. На скільки метрів довжина доріжки більша за її ширину? На скільки метрів ширина доріжки менша від її довжини?
Короткий запис
Довжина — 8 м, на ? менше, ніж ширина
Ширина — 2 м, на ? більше, ніж довжина
Розв’язання
1) 8 – 2 = 6 (м) – на стільки метрів довжина доріжки більша за її ширину
2) 8 – 2 = 6 (м) – на стільки метрів ширина доріжки менша за її довжину
2) Довжина килимової доріжки 8 м, а ширина — 2 м. У скільки разів довжина доріжки більша за її ширину? У скільки разів ширина доріжки менша від її довжини?
Короткий запис
Довжина — 8 м, у ? разів менше, ніж ширина
Ширина — 2 м, у ? разів більше, ніж довжина
Розв’язання
1) 8 : 2 = 4 (разів) – у стільки разів довжина доріжки більша за її ширину
2) 8 : 2 = 4 (рази) – у стільки разів ширина доріжки менша за її довжину
СТОРІНКА 132
Завдання 1 Множення числа 6
6 • 1 = 6 6 • 2 = 2 • 6 = 12 6 • 3 = 3 • 6 = 18 6 • 4 = 6 • 4 = 24
6 • 5 = 5 • 6 = 30 6 • 6 = 30 + 6 = 36 6 • 7 = 36 + 6 = 42
6 • 8 = 42 + 6 = 48 6 • 9 = 48 + 6 = 54 6 • 10 = 54 + 6 = 60
Завдання 2
До кожної рівності на множення можна скласти рівності на ділення (щоб знайти невідомий множник, треба добуток поділити на відомий множник):
6 • 5 = 30 30 : 6 = 5 30 : 5 = 6 6 • 6 = 36 36 : 6 = 6
6 • 7 = 42 42 : 6 = 7 42 : 7 = 6 6 • 8 = 48 48 : 6 = 8 48 : 8 = 6
6 • 9 = 54 54 : 6 = 9 54 : 9 = 6 6 • 10 = 60 60 : 6 = 10 60 : 10 = 6
Кожний наступний результат на 6 більший за попередній, а кожний попередній результат на 6 менший від наступного:
|
6 • 8 = 54 – 6 = 48 6 • 9 = 54 6 • 10 = 54 + 6 = 60 |
6 • 4 = 30 – 6 = 24 6 • 5 = 30 6 • 6 = 30 + 6 = 36 |
|
6 • 6 = 42 – 6 = 36 6 • 7 = 42 6 • 8 = 42 + 6 = 48 |
6 • 5 = 36 – 6 = 30 6 • 6 = 36 6 • 7 = 36 + 6 = 42 |
Переставний закон множення: 6 • 2 = 2 • 6 = 12
6 • 3 = 3 • 6 = 12 6 • 4 = 4 • 6 = 24 6 • 5 = 5 • 6 = 30
Завдання 3 Рівняння
18 : 6 = 3, оскільки 3 • 6 = 18 24 : 6 = 4, оскільки 4 • 6 = 24
30 : 6 = 5, оскільки 5 • 6 = 30 12 : 6 = 2, оскільки 2 • 6 = 12
42 : 6 = 7, оскільки 7 • 6 = 42
Завдання 4 У скільки разів одне число більше або менше за інше
6 < 18 у 3 рази (18 : 6 = 3) 54 > 6 у 9 разів (54 : 6 = 9)
6 < 36 у 6 разів (36 : 6 = 6) З0 > 5 у 6 разів (30 : 5 = 6)
6 < 24 у 4 рази (24 : 6 = 4)
Завдання 5 Перший множник • Другий множник = Добуток
Щоб знайти невідомий множник, треба добуток поділити на відомий множник
6 • 6 = 36 6 • 8 = 48 (оскільки 48 : 6 = 8)
9 • 5 = 45 (оскільки 45 : 5 = 9) 4 • 7 = 28
6 • 3 = 18 (оскільки 18 : 6 = 3) 9 • 4 = 36 (оскільки 36 : 4 = 9)
6 • 7 = 42 5 • 8 = 40 (оскільки 40 : 5 = 8)
6 • 9 = 54 4 • 4 = 16 5 • 7 = 35 (оскільки 35 : 5 = 7)
СТОРІНКА 133
Завдання 1 У скільки разів одне число більше або менше за інше?
6 < 42 у 7 разів (42 : 6 = 7) 28 > 4 у 7 разів (28 : 4 = 7)
5 < 35 у 7 разів (35 : 5 = 7) 54 > 6 у 9 разів (54 : 6 = 9)
6 < 48 у 8 разів (48 : 6 = 8) 45 > 5 у 9 разів (45 : 5 = 9)
Завдання 2 Якщо множник збільшити у декілька разів, тоді добуток теж збільшиться у стільки ж разів:
3 • 5 = 15 9 • 5 = (3 • 3) • 5 = (3 • 5) • 3 = 15 • 3 = 45
6 • 5 = 30 6 • 10 = 6 • (5 • 2) = (6 • 5) • 2 = 30 • 2 = 60
2 • 4 = 8 4 • 4 = (2 • 2) • 4 = (2 • 4) • 2 = 8 • 2 = 16
Завдання 3
1) У Петрика 5 купюр по 10 гривень, а в Єви — 5 купюр по 2 гривні. На скільки менше грошей у Єви, ніж у Петрика?
Короткий запис
Петрик — ?, 5 купюр по 10 грн
Єва — ?, 5 купюр по 2 грн; на ? менше, ніж у Петрика
Схема
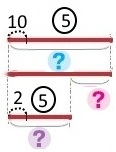
Вираз 10 • 5 – 2 • 5
|
Короткий запис №1 Петрик — ?, 5 купюр по 10 грн |
Короткий запис №2 Єва — ?, 5 купюр по 2 грн |
Короткий запис №3 Петрик — 50 грн Єва — 10 грн, на ? менше |
План розв’язування
1) Скільки гривень у Петрика?
2) Скільки гривень у Єви?
3) На скільки менше грошей у Єви, ніж у Петрика?
Розв’язання
1) 10 • 5 = 50 (грн.) – гривень у Петрика
2) 2 • 5 = 10 (грн.) – гривень у Єви
3) 50 – 10 = 40 (грн.) – на стільки менше грошей у Єви, ніж у Петрика
2 спосіб
Оскільки у дітей однакова кількість купюр, спочатку можна обчислити на скільки гривень менше на одній купюрі дівчинки, а потім для п’яти таких купюр, тоді
Короткий запис
Купюра Петрика — 10 грн
Купюра Єви — 2 грн, на ? менше, ніж на купюрі Петрика
Різниця грошей — ?, 5 купюр по ? грн
Схема
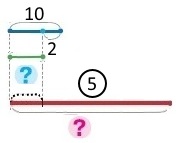
Вираз (10 – 2) • 5
|
Короткий запис №1 Купюра Петрика — 10 грн Купюра Єви — 2 грн, на ? менше |
Короткий запис №2 Різниця грошей — ? грн., 5 купюр по 8 грн
|
План розв’язування
1) На скільки менше грошей на 1 купюрі у Петрика, ніж у Єви?
3) На скільки менше грошей у Єви, ніж у Петрика?
Розв’язання
1) 10 – 2 = 8 (грн.) – на стільки гривень менше на 1 купюрі у Петрика, ніж у Єви
2) 8 • 5 = 40 (грн.) – на стільки менше грошей у Єви, ніж у Петрика
Відповідь: у Єви на 40 гривень менше, ніж у Петрика
2) У Петрика 5 купюр по 10 гривень, а в Єви — 5 купюр по 2 гривні. У скільки разів менше грошей у Єви, ніж у Петрика?
Короткий запис
Петрик — ?, 5 купюр по 10 гривень
Єва — ?, 5 купюр по 2 гривні; у ? разів менше, ніж у Петрика
Схема
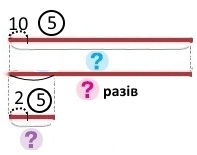
Вираз 10 • 5 : 2 • 5
|
Короткий запис №1 Петрик — ?, 5 купюр по 10 грн |
Короткий запис №2 Єва — ?, 5 купюр по 2 грн |
Короткий запис №3 Петрик — 50 грн Єва — 10 грн, у ? разів менше |
План розв’язування
1) Скільки гривень у Петрика?
2) Скільки гривень у Єви?
3) У скільки разів менше грошей у Єви, ніж у Петрика?
Розв’язання
1) 10 • 5 = 50 (грн.) – гривень у Петрика
2) 2 • 5 = 10 (грн.) – гривень у Єви
3) 50 : 10 = 5 (разів) – у стільки разів менше грошей у Єви, ніж у Петрика
Відповідь: у Єви у 5 разів менше грошей, ніж у Петрика
Завдання 4 Порівняння виразів
6 • 7 + 6 = 6 • 9 – 6 (6 • 7 + 6 = 6 • 9 – 6 = 6 • 8)
6 • 5 + 8 = 5 • 6 + 8 (переставний закон множення)
(12 – 30 : 5) • 7 = 54 – 3 • 4 (42 = 42)
(12 – 30 : 5) • 7 = (12 – 6) • 7 = 6 • 7 = 42 54 – 3 • 4 = 54 – 12 = 42
6 • (20 : 4 • 1) > 3 • (12 : 3 • 2) (30 > 24)
6 • (20 : 4 • 1) = 6 • (5 • 1) = 6 • 5 = 30 3 • (12 : 3 • 2) = 3 • (4 • 2) = 3 • 8 = 24
Завдання 5 Порядок дій
|
(29 + 6 • 7 – 26) : 5 = 9 1) 6 • 7 = 42 2) 29 + 42 = 29 + 1 + 41 = 30 + 41 = 71 3) 71 – 26 = 41 + (30 – 26) = 41 + 4 = 45 4) 45 : 5 = 9 |
30 : 6 • 3 + 46 – 28 = 33 1) 30 : 6 = 5 2) 5 • 3 = 15 3) 15 + 46 = 15 + 5 + 41 = 20 + 41 = 61 4) 61 – 28 = 61 – 21 – 7 = 40 – 7 = 33 |
|
34 + (39 – 5 • 6) • 4 = 70 1) 5 • 6 = 30 2) 39 – 30 = 9 3) 9 • 4 = 36 4) 34 + 36 = (30 + 30) + (4 + 6) = 70 |
61 – 18 : 6 • 4 + 36 = 85 1) 18 : 6 = 3 2) 3 • 4 = 12 3) 61 – 12 = 61 – 11 – 1 = 50 – 1 = 49 4) 49 + 36 = 49 + 1 + 35 = 50 + 35 = 85 |
СТОРІНКА 134
Завдання 1, 2
Множення числа 7: 7 • 1 = 7 7 • 2 = 2 • 7 = 14 7 • 3 = 3 • 7 = 21
7 • 4 = 4 • 7 = 28 7 • 5 = 5 • 7 = 35 7 • 6 = 6 • 7 = 42 7 • 7 = 42 + 7 = 49
7 • 8 = 49 + 7 = 56 7 • 9 = 56 + 7 = 63 7 • 10 = 63 + 7 = 70
Ділення на число 7:
7 : 7 = 1 14 : 7 = 2 21 : 7 = 3 28 : 7 = 4 35 : 7 = 5
42 : 7 = 6 49 : 7 = 7 56 : 7 = 8 63 : 7 = 9 70 : 7 = 10
Завдання 2 До кожної рівності на множення можна скласти рівності на ділення: (щоб знайти невідомий множник, треба добуток поділити на відомий множник):
«Родина» чисел 7, 42 при множенні: 7 • 7 = 42 42 : 7 = 7
«Родина» чисел 7, 8, 56 при множенні: 8 • 7 = 56 7 • 8 = 56 56 : 7 = 8 56 : 8 = 7
«Родина» чисел 7, 9, 63 при множенні: 9 • 7 = 63 7 • 9 = 63 63 : 7 = 9 63 : 9 = 7
«Родина» чисел 7, 10, 70 при множенні: 10 • 7 = 70 7 • 10 = 70 70 : 7 = 10 70 : 10 = 7
У таблиці множення числа 7 кожний наступний результат на 7 більший за попередній, а кожний попередній результат на 7 менший від наступного:
|
7 • 7 = 56 – 7 = 49 7 • 8 = 56 7 • 9 = 56 + 7 = 63 |
7 • 5 = 42 – 7 = 35 7 • 6 = 42 7 • 7 = 42 + 7 = 49 |
|
7 • 2 = 21 – 7 = 14 7 • 3 = 21 7 • 4 = 21 + 7 = 28 |
7 • 9 = 70 – 7 = 63 7 • 10 = 70 7 • 11 = 70 + 7 = 77 |
Переставний закон множення: 7 • 2 = 2 • 7 = 14 7 • 3 = 3 • 7 = 21
7 • 4 = 4 • 7 = 28 7 • 5 = 5 • 7 = 35 7 • 6 = 6 • 7 = 42
Завдання 3
У числовому ряді 42, 14, 35, 21, 48, 28, 49, 70, 56 «зайве» число 48 (не ділиться на 7)
Завдання 4
14 : 7 = 2, оскільки 2 • 7 = 14 28 : 7 = 4, оскільки 4 • 7 = 28
35 : 7 = 5, оскільки 5 • 7 = 35 7 : 7 = 1, оскільки 1 • 7 = 7
42 : 7 = 6, оскільки 6 • 7 = 42 49 : 7 = 7, оскільки 7 • 7 = 49
Завдання 5 Порівняння чисел
У скільки разів одне число більше або менше за інше?
7 < 63 у 9 разів (63 : 7 = 9) 21 > 7 у 3 рази (21 : 7 = 3)
7 < 28 у 4 рази (28 : 7 = 4) 42 > 7 у 6 разів (42 : 7 = 6)
7 < 70 у 10 разів (70 : 7 = 10)
Завдання 6
Якщо b = 7, тоді 49 : b + b – 8 = 49 : 7 + 7 – 8 = 7 + 7 – 6 = 7 + 6 – 7 = 6
Якщо b = 7, тоді (63 + b) : b = (63 + 7) : 7 = 70 : 7 = 10