^{(умови завдань з підручника подані чорним кольором)}

§4,5 Аксіоми, теореми, означення, суміжні кути

Завдання 88 

1) Суміжні кути 1,2

2)

3)

4) Суміжні кути 2,1

Завдання 89

1) Чи можуть два суміжних кути дорівнювати 42° і 148°?

Ні, бо 42° + 148° = 190°, 190° > 180°

2) Чи можуть два суміжних кути дорівнювати 90° і 90°?

Так, бо 90° + 90° = 180°

3) Чи можуть два суміжних кути дорівнювати 166° і 14°?

Так, бо 166° + 14° = 180°

4) Чи можуть два суміжних кути дорівнювати 23° і 156°?

Ні, бо 23° + 156° = 179°, 179° < 180°

 

Завдання 90

1) Чи можуть два суміжних кути дорівнювати 13° і 167°?

Так, бо 13° + 167° = 180°

2) Чи можуть два суміжних кути дорівнювати 5° і 165°?

Ні, бо 5° + 165° = 170°, 170° < 180°

3) Чи можуть два суміжних кути дорівнювати 11° і 179°?

Ні, бо 11° + 179° = 190°, 190° > 180°

4) Чи можуть два суміжних кути дорівнювати 91° і 89°?

Так, бо 91° + 89° = 180°

 

Завдання 91  

Знайдіть суміжний кут.

1) 180° – 5° = 175°

2) 180° – 113° = 67°

 

Завдання 92  

Знайдіть суміжний з кут.

1) 180° – 127° = 53°

2) 180° – 39° = 141°

 

Завдання 93

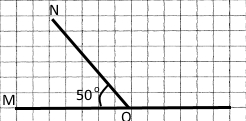
Накресліть за допомогою транспортира ∠MON = 50°. Побудуйте суміжний з ним кут за умови, що ON – їхня спільна сторона. Обчисліть його градусну міру.

180° – 50° = 130°

 

Завдання 94

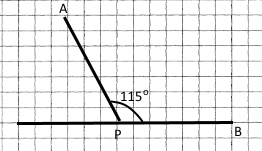
Накресліть за допомогою транспортира кут ∠APB = 115°. Побу­дуйте суміжний з ним кут за умови, що PA – їхня спільна сторона. Обчисліть його градусну міру.

180° – 115° = 65°

 

Завдання 95

Промінь, що проходить між сторонами кута, ділить його на кути, що дорівнюють 15° і 72°. Знайдіть градусну міру кута, суміжного з даним.

15° + 72° = 87° – кут.

180° – 87° = 93° – суміжний кут.  

 

Завдання 96

Бісектриса кута M утворює з його стороною кут, що дорівнює 36°. Знайдіть градусну міру кута, який суміжний з кутом M.

Бісектриса ділить кут пополам, тому

36° • 2 = 72° – кут .

180° – 72° = 108° – суміжний кут. 

 

Завдання 97

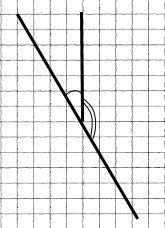
Накресліть два суміжних кути так, щоб їхня спільна сторона була вертикальною, а градусні міри – неоднаковими.

 

Завдання 98

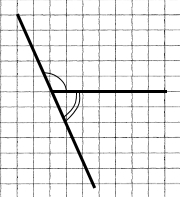
Накресліть два суміжних кути різної градусної міри так, щоб їхня спільна сторона була горизонтальною.

 

Завдання 99

Якщо суміжні кути рівні, то вони прямі. Доведіть це твердження.

Нехай ∠AOK і ∠KOB – суміжні, тоді сума суміжних кутів дорівнює 180°.

∠AOK + ∠KOB = 180°.

Оскільки кути рівні, то рівні їхні градусні міри, тоді

2∠AOK = 180°.

∠AOK = ∠KOB  = 180° : 2 = 90°.

Отже, якщо суміжні кути рівні, то вони прямі.

 

Завдання 100

Кути, суміжні до кутів А і В, рівні між собою. Доведіть, що ∠A = ∠B.

Нехай А₁ – суміжний кут до кута А, В₁ – суміжний кут до кута В. Тоді за теоремою про властивість суміжних кутів маємо: ∠А + ∠А₁ = 180°, ∠В + ∠В₁ = 180°.

∠А + ∠А₁ = ∠В + ∠В₁

Якщо ∠А = ∠В, тоді ∠А₁ = ∠В₁.

Отже, якщо суміжні до кутів рівні, то кути також рівні.

 

Завдання 101 

1) Знайдіть суміжні кути, якщо один з них на 18° менший від іншого.

Нехай х (°) – перший кут, тоді х – 18 (°) – другий кут. За теоремою про суміжні кути складемо рівняння.

х + х – 18 = 180

2х – 18 = 180

х = 180 + 18

х = 198

х = 198 : 2

х = 99 (°) – більший кут.

х – 18 = 99 – 18 = 81 (°) – менший кут.

Відповідь: кути 99° і 81°. 

 

2) Знайдіть суміжні кути, якщо один з них становить 3/7 від іншого.

Нехай х (°) – перший кут, тоді 3/7х (°) – другий кут. За теоремою про суміжні кути складемо рівняння.

х + 3/7х = 180

7/7х + 3/7х = 180

10/7х = 180

х = 180 : 10/7

х = 180 • 7/10

х = 126 (°) – більший кут.

3/7х = 3/7 • 126 = 54 (°) – менший кут.

Відповідь: кути 126° і 54°.

 

Завдання 102

1) Знайдіть суміжні кути, якщо один з них утричі більший за інший.

Нехай х (°) – перший кут, тоді 3х (°) – другий кут. За теоремою про суміжні кути складемо рівняння.

х + 3х = 180

4х = 180

х = 180 : 4  

х = 45 (°) – менший кут.

3х = х • 3 = 45 • 3 = 135 (°) – більший кут.

Відповідь: кути 45° і 135°.

 

2) Знайдіть суміжні кути, якщо один з них становить 25% від іншого.

1) 180 : 100 • 25 = 45 (°) – менший кут.

2) 180 – 45 = 135 (°) – більший кут.

Відповідь: кути 45° і 135°.

 

Завдання 103

Дано гострий кут M і тупий кут N, градусні міри яких від­носяться як 2 : 5. Знайдіть градусні міри цих кутів, якщо кут, суміжний з одним з них, дорівнює 140°.

Кут 140° – тупий, тоді він суміжний з гострим кутом, тобто з М.

1) 180 – 140 = 40 (°) – кут М.

2) 40 : 2 = 20 (°) – припадає на 1 частину. 

3) 20 • 5= 100 (°) – кут N.

Відповідь: ∠M = 40°, ∠N = 100°

 

Завдання 104

Дано тупий кут A і гострий кут B, градусні міри яких від­носяться як 4 : 3. Знайдіть градусні міри цих кутів, якщо кут, суміжний з одним з них, дорівнює 80°.

Кут 80° – гострий, тоді він суміжний з тупим кутом, тобто з А.

1) 180 – 80 = 100 (°) – кут А.

2) 100 : 4 = 25 (°) – припадає на 1 частину. 

3) 25 • 3 = 75 (°) – кут В.

Відповідь: ∠А = 100°, ∠В = 75°

 

Завдання 105

Знайдіть кут між бісектрисами суміжних кутів.

Суміжні кути дорівнюють 180°. Бісектриса кута ділить його пополам, тому кут між бісектрисами дорівнює 180 : 2 = 90°. 

 

Завдання 106

Два кути відносяться як 1 : 2, а суміжні з ними - як 7 : 5. Знайдіть ці кути.

Нехай х (°) – один кут, тоді 2х (°) – другий кут, тоді 180 – х (°) – один суміжний кут, 180 – 2х (°) – другий суміжний кут. Складемо рівняння.

(180 – х)/(180 – 2х) = 7/5

5(180 – х) = 7(180 – 2х)

900 – 5х = 1260 – 14х

14х – 5х = 1260 – 900

9х = 360

х = 360 : 9

х = 40 (°) – один кут.

2х = 40 • 2 = 80 (°) – другий кут.  

Відповідь: кути 40° і 80°.

   

Завдання 107

Один з двох даних кутів на 20° більший за інший, а суміжні з ними – відносяться як 5 : 6. Знайдіть дані кути.

6 – 5 = 1 (ч.) – на стільки частин більший суміжний кут меншого кута. Оскільки відповідний кут менший на 20°, тоді на 1 частину припадає 20°.    

1) 20 • 5 = 100 (°) – менший суміжний кут.

2) 180 – 100 = 80 (°) – більший до нього кут.

Відповідь: кути 80° і 60°. 

 

Завдання 108

Один із суміжних кутів удвічі більший за різницю цих кутів. Знайдіть ці кути.

І варіант

Нехай х (°) – один кут, тоді 180 – х (°) – другий кут, тоді 180 – х – х = 180 – 2х (°) – різниця кутів. Складемо рівняння.

(180 – х) = 2 (180 – 2х)

180 – х = 360 – 4х

4х – х = 360 – 180

3х = 180

х = 180 : 3

х = 60 – один кут.

180 – 60 = 120 – інший кут.

ІІ варіант  

Нехай х (°) – один кут, тоді 180 – х (°) – другий кут, тоді 180 – х – х = 180 – 2х (°) – різниця кутів. Складемо рівняння.

х = 2(180 – 2х)

х = 360 – 4х

х + 4х = 360

5х = 360

х = 360 : 5

х = 72(°) – один кут.

180 – 72 = 108 (°) – інший кут.

Відповідь: кути 60° і 120° або 72° і 108°.

 

Вправи для повторення

Завдання 109

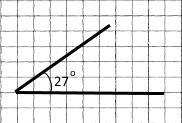
1) Накресліть кут, градусна міра якого дорівнює 27°.

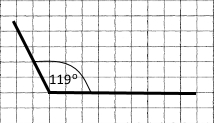
2) Накресліть кут, градусна міра якого дорівнює 119°.

 

Завдання 110

Точки A, B і C лежать на одній прямій, AB = 2,7 см, BC = 3,6 см.

1) Чи може відстань між точками A і C дорівнювати 0,8 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

3,6 = 2,7  + х

х = 3,6 – 2,7

х = 0,9

Ні. 

2) Чи може відстань між точками A і C дорівнювати 0,9 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

3,6 = 2,7  + х

х = 3,6 – 2,7

х = 0,9

Так.

3) Чи може відстань між точками A і C дорівнювати 1 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

3,6 = 2,7  + х

х = 3,6 – 2,7

х = 0,9

Ні.

4) Чи може відстань між точками A і C дорівнювати 6,1 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

2,7  + 3,6 = 6,3

6,3 ≠ 6,1

Ні.

5) Чи може відстань між точками A і C дорівнювати 6,3 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

2,7  + 3,6 = 6,3

Так.

6) Чи може відстань між точками A і C дорівнювати 6,5 см?

Найбільша відстань має дорівнювати сумі двох інших відстаней.

2,7  + 3,6 = 6,3

6,3 ≠ 6,5

Ні.

 

Життєва математика

Завдання 111

Будівельникам для встановлення башти потрібно залити фундамент у формі кільця. Радіус зовніш­нього кола цього фундаменту має дорівнювати 15 м, а внутрішнього – 10 м. Визначте площу земельної ділянки під фундаментом башти.

S₁ = πR₁²

S₂ = πR₂²

пR₁ – пR₂ = п (R₁ – R₂) = 3,14 • (15 – 10) = 15,7 (м²) 

 

Завдання 112

1) ТУК — КУТ                             2) АРЯМП — ПРЯМА

3) КЛЕІВД — ЕВКЛІД                   4) МОРТЕІЯГЕ — ГЕОМЕТРІЯ

Інші завдання дивись тут...