© Барна Р., 2020
Серія "Вчимось разом" до підручника "Математика 3 клас Козак М., Корчевська О."
Завдання 293
Множення перевіряємо діленням. Ділення перевіряємо множенням і діленням.
|
Обчислення |
Перевірка |
|
480 : 3 = (300 + 180) : 3 = 100 + 60 = 160 25 • 4 = (20 + 5) • 4 = 80 + 20 = 100 96 : 6 = (60 + 36) : 6 = 10 + 6 = 16 720 : 4 = (400 + 320) : 4 = 100 + 80 = 180 |
160 • 3 = (100 + 60) • 3 = 300 + 180 = 480 100 : 4 = (80 + 20) : 4 = 20 + 5 = 25 16 • 6 = (10 + 6) • 6 = 60 + 36 = 96 180 • 4 = (100 + 80) • 4 = 400 + 360 = 720 |
Завдання 294 Одиниці вимірювання
578 кг = 500 кг + 78 кг = 5 ц 78 кг
240 кг = 200 кг + 40 кг = 2 ц 40 кг
705 кг = 700 кг + 5 кг = 7 ц 5 кг
Завдання 295
1) Складена задача на знаходження третього числа за сумою двох інших
Першого дня кіоск продав 250 зошитів, другого – на 80 більше. Третього дня кіоск продав у 2 рази менше зошитів, ніж першого і другого разом. Скільки зошитів продав магазин третього дня?
|
І день |
ІІ день |
ІІІ день |
Всього |
|
250 зошитів |
на 80 зошитів більше, ніж І дня |
У 2 рази менше, ніж І і ІІ дні разом |
? |
Короткий запис
І день — 250 зошитів
ІІ день — ?, на 80 зошитів більше, ніж І дня
Всього (І і ІІ день) — ?
ІІІ день — ?, у 2 рази менше, ніж І і ІІ дні разом

Вираз (250 + (250 + 80)) • 2
|
Короткий запис №1 І день — 250 зошитів ІІ день — ?, на 80 зошитів більше |
Короткий запис №2 І день — 250 зошитів ІІ день — 330 зошитів Всього — ? |
Короткий запис №3 І і ІІ день — 580 зошитів ІІІ день — ?, у 2 рази менше |
План розв’язування
1) Скільки зошитів продав магазин І дня?
2) Скільки зошитів продав магазин за І і ІІ дні разом?
3) Скільки зошитів продав магазин третього дня?
Розв’язання
1) 250 + 80 = 250 + 50 + 30 = 330 (з.) – зошитів продав магазин І дня.
2) 250 + 330 = 500 + 80 = 580 (з.) – зошитів продав магазин ІІ дня.
3) 580 : 2 = (400 + 180) : 2 = 290 (з.) – зошитів продав магазин третього дня.
Відповідь: третього дня магазин продав 290 зошитів.
2) Складена задача на знаходження невідомого доданку
За два дні у кіоску продали 320 зошитів. Першого дня – 1/4 усіх зошитів. Скільки зошитів продали другого дня?
|
І день |
ІІ день |
Всього |
|
1/4 усіх зошитів |
? |
320 зошитів |
Короткий запис
І день — ?, 1/4 всього
ІІ день — ?
Всього — 320 зошитів
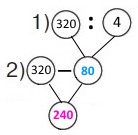
Вираз 320 – 320 : 4
|
Короткий запис №1 І день — ?, 1/4 від 320 зошитів |
Короткий запис №2 І день — 80 зошитів ІІ день — ? Всього — 320 зошитів |
План розв’язування
1) Скільки зошитів продали першого дня?
2) Скільки зошитів продали другого дня?
Розв’язання
1) 320 : 4 = 80 (з.) – зошитів продали першого дня.
2) 320 – 80 = 320 – 100 + 20 = 240 (з.) – зошитів продали другого дня.
Відповідь: другого дня продали 240 зошитів.
Завдання 296 Складена задача на зведення до одиниці
Двоє мулярів працювали з однаковою продуктивністю. Перший муляр за 7 днів змурував 14 м кам'яної огорожі. Скільки метрів огорожі змурував другий муляр за 5 днів?
|
Муляри |
Продуктивність (метрів за 1 день) |
Час роботи (дні) |
Загальний виробіток (метрів огорожі) |
|
І |
? |
7 |
14 |
|
ІІ |
однакова |
5 |
? |
Короткий запис
І муляр — 7 днів — 14 м
1 день — ? м
ІІ муляр — 5 днів — ? м
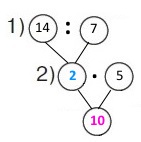
Вираз 14 : 7 • 5
План розв’язування
1) Скільки метрів огорожі мурує муляр за день?
2) Скільки метрів огорожі змурував другий муляр за 5 днів?
Розв’язання
1) 14 : 7 = 2 (м) – метрів огорожі мурує муляр за день.
2) 2 • 5 = 10 (м) – метрів огорожі змурував другий муляр за 5 днів.
Відповідь: другий муляр змурував 10 метрів огорожі.
Завдання 297 Точки А і D — центри кіл, радіуси яких дорівнюють 4 см. Визнач довжини відрізків АС, СВ, BD, якщо довжина відрізка AD — 6 см.
АВ = СD = 4 см – радіуси кіл.
АС = АD – СD = 6 см – 4 см = 2 см
СВ = АD – АВ = 6 см – 4 см = 2 см
ВD = АD – АВ = 6 см – 4 см = 2 см
Завдання 298
Є три відрізки: Так, Ток і Тук. Відрізок Так містить 4 Туки, а відрізок Ток — З Туки. Відрізки Так і Ток з'єднали в один. Визначте його довжину в Туках, а потім — у сантиметрах, якщо відомо, що 1 Тук = 2 см.
1 Так = 4 Туки = 1 Тук • 4 = 2 см • 4 = 8 см
1 Ток = 3 Туки = 1 Тук • 3 = 2 см • 3 = 6 см
1 Так + 1 Ток = 8 см + 6 см = 14 м
2 спосіб
1 Так + 1 Ток = 4 Туки + 3 Туки = 7 Туків = 1 Тук • 7 = 2 см • 7 = 14 см
Відповідь: 12 см
Завдання 299 Складена задача на знаходження частини числа
Чотири білочки збирали гриби. Перша знайшла 29 грибів, друга — у З рази більше, третя — на 13 грибів більше, ніж друга, а четверта — половину кількості того, що знайшла третя. Скільки грибів знайшла четверта білочка?
Короткий запис
Перша білочка — 29 грибів
Друга білочка — ?, у 3 рази більше, ніж І білочка
Третя білочка — ?, на 13 грибів більше, ніж ІІ білочка
Четверта білочка — ?, 1/2 грибів третьої білочки
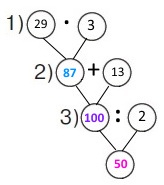
Вираз (29 • 3 + 13) : 2
План розв’язування
1) Скільки грибів знайшла друга білочка?
2) Скільки грибів знайшла третя білочка?
3) Скільки грибів знайшла четверта білочка?
Розв’язання
1) 29 • 3 = (20 + 9) • 3 = 87 (гр.) – грибів знайшла друга білочка.
2) 87 + 13 = 90 + 10 = 100 (гр.) – грибів знайшла третя білочка.
3) 100 : 2 = 50 (гр.) – грибів знайшла третя білочка.
Відповідь: третя білочка знайшла 50 грибів.
Завдання 300
125 см = 100 см + 25 см = 1 м 25 см
7 ц 8 кг = 1 ц • 7 + 8 кг = 100 кг • 7 + 8 кг = 708 кг
368 кг = 300 кг + 68 кг = 3 ц 68 кг
6 м 20 см = 1 м • 6 + 20 см = 100 см • 6 + 20 см = 620 см
306 мм = 300 мм + 6 мм = 3 дм 6 мм
306 мм = 300 мм + 6 мм = 30 см 6 мм
Завдання 301
|
Множення і ділення |
Перевірка |
|
19 • 4 = (10 + 9) • 4 = 40 + 36 = 76 160 : 80 = 16 : 8 = 2 7 • 14 = 7 • (10 + 4) = 70 + 28 = 98 920 : 20 = (800 + 120) : 20 = 40 + 6 = 46 |
76 : 4 = (40 + 36) : 4 = 10 + 9 = 19 2 • 80 = 160 98 : 7 = (70 + 28) : 7 = 10 + 4 = 14 46 • 20 = (40 + 6) • 20 = 800 + 120 = 920 |
Завдання 302
Множник • Множник = Добуток
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
5 • 150 = 5 • (100 + 50) = 500 + 250 = 750
130 • 4 = 520 (бо 520 : 4 = (400 + 120) : 4 = 100 + 30 = 130)
80 • 12 = 960 (бо 960 : 80 = 96 : 8 = (80 + 16) : 8 = 10 + 2 = 12)
7 • 60 = 420 (бо 420 : 7 = 60)
13 • 30 = 390 (бо 390 : 30 = 39 : 3 = (30 + 9) : 3 = 10 + 3 = 13)
240 • 3 = (200 + 40) • 3 = 600 + 120 = 720
16 • 40 = (10 + 6) • 40 = 400 + 240 = 640
30 • 25 = 30 • (20 + 5) = 600 + 150 = 750
Завдання 303 Складена задача на множення
Є 3 будинки: перший має 16 поверхів, другий — у 4 рази менше, а третій — у 2 рази більше, ніж другий. У третьому будинку на кожному поверсі 12 квартир. Скільки квартир у третьому будинку?
|
Будинки |
Квартир на 1 поверсі |
Кількість поверхів |
Загальна кількість квартир |
|
І |
|
16 |
|
|
ІІ |
|
?, у 4 рази менше, ніж на І |
|
|
ІІІ |
12 |
?, у 2 рази більше, ніж на ІІ |
? |
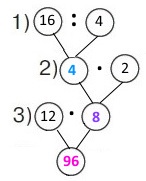
Вираз 12 • (16 : 4 • 2)
|
Короткий запис №1 І будинок — 16 поверхів ІІ будинок — ?, у 4 рази менше |
Короткий запис №2 ІІ будинок — 4 поверхи ІІІ будинок — ?, у 2 рази більше |
Короткий запис №3 У ІІІ будинку — ? кв., 8 поверхів по 12 квартир |
План розв’язування
1) Скільки поверхів у другому будинку?
2) Скільки поверхів у третьому будинку?
3) Скільки квартир у третьому будинку?
Розв’язання
1) 16 : 4 = 4 (п.) – поверхів у другому будинку.
2) 4 • 2 = 8 (п.) – поверхів у третьому будинку.
3) 12 • 8 = (10 + 2) • 8 = 96 (кв.) – квартир у третьому будинку.
Відповідь: у третьому будинку 96 квартир.
Завдання 304 Маса 4 однакових телят 280 кг Порося у 2 рази легше (менше кілограмів) за теля. Визнач масу двох таких поросят.
|
Тварина |
Маса 1 тварини (кг) |
Кількість тварин |
Загальна маса (кг) |
|
Теля |
? |
4 |
280 |
|
Порося |
?, у 2 рази менше |
2 |
? |
Короткий запис
4 телята — 280 кг, 1 теля — ?
5 поросят — ? кг, 1 порося — ?, у 2 рази менше
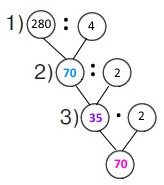
Вираз 280 : 4 : 2 • 2
План розв’язування
1) Яка маса теля?
2) Яка маса порося?
3) Визнач масу двох таких поросят.
Розв’язання
1) 280 : 4 = 70 (кг) – маса теля.
2) 70 : 2 = (60 + 10) : 2 = 35 (кг) – маса порося.
3) 35 • 2 = 35 + 35 = 70 (кг) – маса двох поросят.
2 спосіб (логічний).
Якщо порося важить половину теля, тоді два поросяти важать як одне теля, тому
280 : 4 = 70 (кг) – маса теля або двох поросят.
Відповідь: маса двох поросят 70 кілограмів.
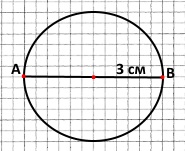
Завдання 305 Довжина відрізка АВ 6 см. Його середина — центр кола радіусом З см. Накресли відрізок і коло. Як можна назвати відрізок АВ?
АВ – діаметр кола.
Завдання 306 Порядок дій
|
(З • 60 + 120) : 5 : 4 = 15 1) 3 • 60 = 180 2) 180 + 120 = 300 3) 300 : 5 = 60 4) 60 : 4 = (40 + 20) : 4 = 15 |
240 + (740 – 1000 : 20) = 930 1) 1000 : 20 = 100 : 2 = 50 2) 740 – 50 = 690 3) 240 + 690 = 930 |
Завдання 307
782 мм = 700 мм + 82 мм = 7 дм 82 мм
782 мм = 780 мм + 2 мм = 78 см 2 мм
541 см = 500 см + 41 см = 5 м 41 см
541 см = 540 см + 1 см = 54 дм 1 см
Завдання 308
75 : 3 • 4 = (60 + 15) : 3 • 4 = (20 + 5) • 4 = 80 + 20 = 100
6 • 15 : 5 = 15 : 5 • 6 = 3 • 6 = 18
80 : 5 • 6 = (50 + 30) : 5 • 6 = (10 + 6) • 6 = 60 + 36 = 96
7 • 12 : 6 = 12 : 6 • 7 = 2 • 7 = 14
90 : 5 • 4 = (50 + 40) : 5 • 4 = (10 + 8) • 4 = 40 + 32 = 72
6 • 14 : 7 = 14 : 7 • 6 = 2 • 6 = 12
Завдання 309 Складена задача на знаходження невідомого доданку
У лісі росло 160 сосен — це 1/4 всіх хвойних дерев лісу. Решта – ялини. Скільки ялин у лісі?
Короткий запис
Сосни — 160 дерев, це 1/4 всього
Ялини — ?
Всього — ?

Вираз 160 • 4 – 160
Розв’язання
Якщо 160 дерев – це вже 1/4 всіх хвойних дерев, тоді
1) 160 • 4 = (100 + 60) • 4 = 640 (д.) – всіх дерев у лісі.
2) 640 – 160 = 640 – 200 + 40 = 480 (ял.) – ялин у лісі.
2 спосіб
Оскільки в хвойному лісі ростуть сосни і ялини, а 160 сосен – це одна з чотирьох частин, тоді ялин буде 3 таких частини, тому
160 • 3 = (100 + 60) • 3 = 480 (ял.) – ялин у лісі.
Відповідь: у лісі 480 ялин.