© Барна Р., 2020
Серія "Вчимось разом" до підручника
"Математика 3 клас Скворцова С., Онопрієнко О. (частина 2)"
Сторінка 53
Завдання 4 Порозрядне додавання та віднімання з переходом через десяток
580 + 230 = (500 + 80) + (200 + 30) = (500 + 200) + (80 + 30) = 700 + 110 = 810
520 – 450 = (400 + 120) – (400 + 50) = (400 – 400) + (120 – 50) = 0 + 70 = 70
770 – 490 = (600 + 170) – (400 + 90) = (600 – 400) + (170 – 90) = 200 + 80 = 280
380 + 250 = (300 + 80) + (200 + 50) = (300 +200) + (80 + 50) = 500 + 130 = 630
640 + 170 = (600 + 40) + (100 + 70) = (600 + 100) + (40 + 70) = 700 + 110 = 810
700 – 360 = (600 + 100) – (300 + 60) = (600 – 300) + (100 – 60) = 300 + 40 = 340
810 – 640 = (700 + 110) – (600 + 40) = (700 – 600) + (110 – 40) = 100 + 70 = 170
370 + 560 = (300 + 70) + (500 + 60) = (300 + 500) + (70 + 60) = 800 + 130 = 930
Завдання 5 Складена задача на множення
Із відрізу тканини пошили 9 спідниць, витративши на кожну 2 м тканини. Скільки суконь можна було б пошити з цього відрізу, витрачаючи на кожну сукню 3 м тканини?
1 спосіб (арифметичний метод розв'язування)
|
|
Кількість метрів на 1 виріб |
Кількість виробів |
Загальна кількість метрів |
|
спідниці |
2 |
9 |
? |
|
сукні |
3 |
? |
однаково |
|
Короткий запис №1 Відріз — ? м., 9 спідниць по 2 м |
Короткий запис №2 Сукні — ? с., 18 м уміщають по 3 м |
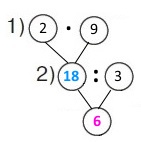
Вираз 2 • 9 : 3
Розв'язання
1) 2 • 9 = 18 (м) – метрів у відрізі.
2) 18 : 3 = 6 (с.) – суконь можна було би пошити.
2 спосіб (алгебраїчний метод розв'язування )
|
|
Кількість метрів на 1 виріб |
Кількість виробів |
Загальна кількість метрів |
|
спідниці |
2 |
9 |
2 • 9 |
|
сукні |
3 |
а |
3 • а |
Нехай а (с.) – кількість суконь, тоді 3 • а (м) – метрів у відрізі, також 2 • 9 (м) – метрів у відрізі. Складемо рівняння.
3 • а = 2 • 9
3 • а = 18
а = 18 : 3
а = 6 (с.)
Відповідь: із цього відрізу можна було би пошити 6 суконь.
Завдання 6 Порядок дій
|
430 + 190 – (830 – 340) : 7 • 3 = 410 1) 830 – 340 = 830 – 330 – 10 = 500 – 10 = 490 2) 490 : 7 = 70 3) 70 • 3 = 210 4) 430 + 190 = 500 + 120 = 620 5) 620 – 210 = 410 |
180 + 640 : 8 • 4 – 630 : 70 • 10 = 410 1) 640 : 8 = 80 2) 80 • 4 = 320 3) 630 : 70 = 9 4) 9 • 10 = 90 5) 180 + 320 = 400 + 100 = 500 6) 500 – 90 = 410 |
|
(90 • 6 – 50) : 70 + 3 • 30 • 9 – 17 = 800 1) 90 • 6 = 540 2) 540 – 50 = 540 – 40 – 10 = 500 – 10 = 490 3) 490 : 70 = 7 4) 3 • 30 = 90 5) 90 • 9 = 810 6) 810 + 7 = 817 7) 817 – 17 = 800 |
(70 • 3 – 9 • 20) : 10 • 60 : 30 = 6 1) 70 • 3 = 210 2) 9 • 20 = 180 3) 210 – 180 = 210 – 110 – 70 = 100 – 70 = 30 4) 30 : 10 = 3 5) 3 • 60 = 180 6) 180 : 30 = 6 |
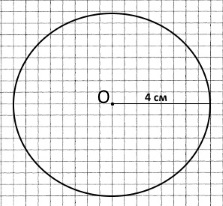
Завдання 7 Визнач радіус кола діаметром 8 см. Накресли це коло.
8 см : 2 = 4 см – радіус кола.
Завдання 8 Рівняння
|
5 • 80 = 400 490 : 7 = 70 80 • 9 = 720 6 • 60 = 360 280 : 7 = 40 60 • 9 = 540 810 : 90 = 9 560 : 8 = 70 |
60 • 10 = 600, оскільки 600 : 60 = 10 450 : 50 = 9, оскільки 450 : 9 = 50 360 : 6 = 60, оскільки 60 • 6 = 360 60 • 3 = 180, оскільки 180 : 3 = 60 120 : 2 = 60, оскільки 60 • 2 = 120 630 : 70 = 9, оскільки 630 : 9 = 70 6 • 20 = 120, оскільки 120 : 6 = 20 360 : 90 = 4, оскільки 4 • 90 = 360 |
Завдання 9 У двох кошиках 75 слив. Коли з першого кошика взяли 6 слив, а з другого — 9 слив, то в кошиках залишилося слив порівну. Скільки слив було в кожному кошику спочатку?
Розв'язання
1) 6 + 9 = 15 (сл.) – всього слив забрали.
2) 75 – 15 = 60 (сл.) – слив залишилось порівну у ящиках.
3) 60 : 2 = 30 (сл.) – слив залишилось у кожному ящику.
4) 30 + 6 = 36 (сл.) – слив було в першому ящику спочатку.
5) 30 + 9 = 39 (сл.) – слив було у другому ящику спочатку.
Відповідь: спочатку в першому ящику було 36 слив, у другому – 39 слив.
Сторінка 54
Завдання 1
1) Додавання частинами:
350 + 480 = 350 + (400 + 80) = (350 + 400) + 80 = 750 + 80 = 830
350 + 480 = 350 + (50 + 430) = (350 + 50) + 430 = 400 + 430 = 830
350 + 480 = (300 + 50) + 480 = (300 + 480) + 50 = 780 + 50 = 830
350 + 480 = (330 + 20) + 480 = 330 + (20 + 480) = 330 + 500 = 830
350 + 480 = (300 + 50) + (400 + 80) = (300 + 400) + (50 + 80) = 700 + 130 = 830
350 + 480 = 350 + (500 – 20) = (350 + 500) – 20 = 850 – 20 = 830
2) Віднімання частинами:
540 – 360 = 540 – (300 + 60) = 540 – 300 – 60 = 240 – 60 = 180
540 – 360 = 540 – (340 + 20) = 540 – 340 – 20 = 200 – 20 = 180
540 – 360 = (500 + 40) – 360 = (500 – 360) + 40 = 140 + 40 = 180
540 – 360 = (80 + 460) – 360 = 80 + (460 – 360) = 80 + 100 = 180
540 – 360 = (400 + 140) – (300 + 60) = (400 – 300) + (140 – 60) = 100 + 80 = 180
540 – 360 = 540 – (400 – 40) = 540 – 400 + 40 = 140 + 40 = 180
Завдання 2
730 – 480 = 730 – 430 – 50 = 300 – 50 = 250
460 + 270 = (400 + 200) + (60 + 70) = 600 + 130 = 730
540 + 190 = 540 + (100 + 90) = 540 + 100 + 90 = 640 + 90 = 730
640 – 450 = 640 – 440 – 10 = 200 – 10 = 190
810 – 490 = (700 + 110) – (400 + 90) = (700 – 400) + (110 – 90) = 300 + 20 = 320
360 + 360 = (300 + 300) + (60 + 60) = 600 + 120 = 720
240 + 670 = (200 + 600) + (40 + 70) = 800 + 110 = 910
820 – 750 = (700 + 120) – (700 + 50) = (700 – 700) + (120 – 50) = 70
Завдання 3
|
720 : 8 = 90 210 : 70 = 3 7 • 70 = 490 9 • 100 = 900 |
300 : 50 = 6, оскільки 6 • 50 = 300 40 • 8 = 320, оскільки 320 : 8 = 40 160 : 2 = 80, оскільки 160 : 80 = 2 40 • 9 = 360, оскільки 360 : 40 = 9 |
Завдання 4 Ціна, кількість, вартість
Складена задача на ділення
Вартість трьох ялинкових прикрас і вартість чотирьох пакетів «дощику» — однакові. Ціна однієї прикраси становить 8 гривень. Визнач ціну пакета «дощику».
|
Товар |
Ціна (грн) |
Кількість |
Вартість (грн) |
|
Ялинкові прикраси |
8 |
3 |
? |
|
Пакети «дощику» |
? |
4 |
однаково |
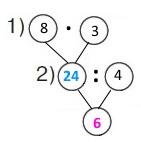
Вираз (8 • 3) : 4
Розв'язання
1) 8 • 3 = 24 (грн) – вартість пакета «дощику» (ялинкової прикраси).
2) 24 : 4 = 6 (грн) – ціна пакета «дощику».
Відповідь: ціна пакета «дощику» 6 гривень.
Обернена задача на знаходження числа 8
Вартість трьох ялинкових прикрас і вартість чотирьох пакетів «дощику» — однакові. Ціна одного пакета «дощику» становить 6 гривень. Визнач ціну ялинкової прикраси.
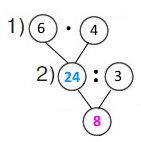
Вираз (6 • 4) : 3
Розв'язання
1) 6 • 4 = 24 (грн) – вартість ялинкової прикраси (пакета «дощику»).
2) 24 : 3 = 8 (грн) – ціна ялинкової прикраси.
Відповідь: ціна ялинкової прикраси 8 гривень.
Обернена задача на знаходження числа 4
Вартість трьох ялинкових прикрас і вартість декількох пакетів «дощику» — однакові. Ціна однієї прикраси становить 8 гривень, а пакета «дощику» – 6 грн. Скільки пакетів «дощику» купили?
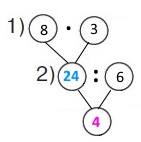
Вираз (8 • 3) : 6
Розв'язання
1) 8 • 3 = 24 (грн) – вартість пакета «дощику» (ялинкової прикраси).
2) 24 : 6 = 4 (п.) – пакетів «дощику» купили.
Відповідь: купили 4 пакети «дощику».
Обернена задача на знаходження числа 3
Вартість 4 пакетів «дощику» і вартість декількох ялинкових прикрас — однакові. Ціна однієї прикраси становить 8 гривень, а пакета «дощику» – 6 грн. Скільки ялинкових прикрас купили?
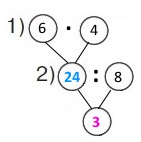
Вираз (6 • 4) : 8
Розв'язання
1) 6 • 4 = 24 (грн) – вартість ялинкової прикраси (пакета «дощику»).
2) 24 : 8 = 3 (п.) – ялинкових прикрас купили.
Відповідь: купили 3 ялинкові прикраси.
Сторінка 55
Завдання 1
1) Складена задача на ділення на вміщення
За 3 книжки заплатили 240 грн. Ціна книжок і квитків до театру однакова. Скільки квитків до театру можна придбати на 480 грн?
|
Товар |
Ціна (грн) |
Кількість |
Вартість (грн) |
|
Книжки |
? |
3 |
240 |
|
Квитки |
однакова |
? |
480 |
Коротка умова
Книжки — 3 штуки — 240 грн
Квитки — ? штук — 480 грн
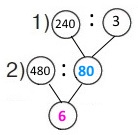
Вираз 480 : (240 : 3)
Розв'язання
1) 240 : 3 = 80 (грн) — ціна квитка (книжки).
2) 480 : 80 = 6 (кв.) – квитків можна придбати.
Відповідь: до театру можна придбати 6 квитків.
2) Складена задача на ділення
Для нагородження переможців шкільного конкурсу читців виділили деяку суму грошей. На ці гроші можна купити або 3 книжки, по 80 грн за кожну, або 6 квитків до театру. Яка ціна одного квитка до театру?
|
Товар |
Ціна (грн) |
Кількість (шт.) |
Вартість (грн) |
|
Книжки |
80 |
3 |
? |
|
Квитки |
? |
6 |
однакова |
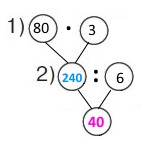
Вираз (80 • 3) : 6
Розв'язання
1) 80 • 3 = 240 (грн) – вартість квитків (книжок).
2) 240 : 6 = 40 (грн) – ціна квитка до театру.
Відповідь: ціна квитка до театру 40 гривень.
3) Складена задача на ділення
Для нагородження переможців конкурсу бальних танців купили однакову кількість книжок і квитків до театру. За книжки ціною 80 грн кожна заплатили 240 грн. Яка ціна квитка, якщо за всі квитки заплатили 300 грн?
|
Товар |
Ціна (грн) |
Кількість (шт.) |
Вартість (грн) |
|
Книжки |
80 |
? |
240 |
|
Квитки |
? |
однакова |
300 |
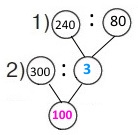
Вираз 300 : (240 : 80)
Розв'язання
1) 240 : 80 = 3 (шт.) — купили квитків (книжок).
2) 300 : 3 = 100 (грн) – ціна квитка.
Відповідь: ціна квитка 100 гривень.
Сторінка 56
Завдання 2 Складена задача на множення
Купили однакову кількість кілограмів яблук і слив. Ціна кілограма яблук — 6 грн, а слив — 10 грн. Знайди вартість яблук, якщо вартість слив становила 20 грн.
|
Товар |
Ціна (грн) |
Кількість |
Вартість (грн) |
|
Яблука |
6 |
однакова |
? |
|
Сливи |
10 |
? |
20 |
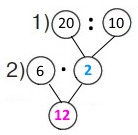
Вираз 6 • (20 : 10)
План розв’язування
1) Скільки кілограмів яблук (слив) купили?
2) Знайди вартість яблук.
Розв'язання
1) 20 : 10 = 2 (кг) — кілограмів яблук (слив) купили.
2) 6 • 2 = 12 (грн) – вартість яблук.
Відповідь: вартість яблук 12 гривень.
Завдання 3
440 + 270 = 440 + 200 + 70 = 640 + 70 = 710
550 – 260 = 550 – 250 – 10 = 300 – 10 = 290
430 + 290 = (400 + 200) + (30 + 90) = 600 + 120 = 720
620 – 450 = (500 + 120) – (400 + 50) = (500 – 400) + (120 – 50) = 100 + 70 = 170
360 + 270 = 360 + (300 – 30) = 360 + 300 – 30 = 660 – 30 = 630
540 – 280 = 540 – (300 – 20) = 540 – 300 + 20 = 240 + 20 = 260
670 + 180 = 670 + 30 + 150 = 700 + 150 = 850
910 – 770 = 910 – 710 – 60 = 200 – 60 = 140
350 + 270 = (300 + 200) + (50 + 70) = 500 + 120 = 620
430 – 270 = (300 + 130) – (200 + 70) = (300 – 200) + (130 – 70) = 100 + 60 = 160
280 + 280 = (200 + 200) + (80 + 80) = 400 + 160 = 560
810 – 650 = 810 – 610 – 40 = 200 – 40 = 160
Завдання 4 У двох коробках 84 цукерки. Коли з першої коробки взяли 44 цукерки, а з другої — 30 цукерок, то в коробках залишилося цукерок порівну. Скільки цукерок було в кожній коробці спочатку?
Розв'язання
1) 44 + 30 = 74 (ц.) – всього цукерок забрали.
2) 84 – 74 = 10 (ц.) – залишилось цукерок порівну в коробках.
3) 10 : 2 = 5 (ц.) – залишилось цукерок у кожній коробці.
4) 5 + 44 = 49 (ц.) – цукерок було у першій коробці спочатку.
5) 5 + 30 = 35 (ц.) – цукерок було у другій коробці спочатку.
Відповідь: спочатку в першій коробці було 49 цукерок, у другій – 35 цукерок.