КОМБІНОВАНА КОНТРОЛЬНА РОБОТА № 8 Варіант 1
Завдання 1 Серед чисел (59 067, 90 659, 906 248, 349 060) число, у якому 906 сотень та розклади на розрядні доданки
90659
Міркуємо так
90659 = 906 сот 5 дес. 9 од.
90659 = 90000 + 600 + 50 + 9
Завдання 2 1/9 від числа 186 885
|
186885 : 9 = 20765 Відповідь: 20765 |
_186885 | 9 18 20765 _68 63 _58 54 _45 45 0 |
Завдання 3 Рівняння
х + 1500 = 40 • 50
х + 1500 = 2000
x = 2000 - 1500
x = 500
Завдання 4 Значення виразу, якщо х = 47
20 000 - 28 • 75 + а + 989 = 17676
Якщо х = 47, тоді 20000 – 28 • 75 + х + 989 = 20000 – 28 • 75 + 47 + 989=18936
|
х 28 75 140 196 2100 |
_ 20000 2100 17900 |
+ 17900 47 17947 |
+ 17947 989 18936 |
Завдання 5
150 хв = 2 год 30 хв
2 год 6 хв = 126 хв
3 доби 4 год = 76 год
Міркуємо так
150 хв = 120 хв + 30 хв = (120 : 60) год + 30 хв = 2 год 30 хв
2 год 6 хв = 2 • 1 год + 6 хв = 2 • 60 хв + 6 хв = 120 хв + 6 хв = 126 хв
3 доби 4 год = 3 • 1 доба + 4 год = 3 • 24 год + 4 год = 72 год + 4 год = 76 год
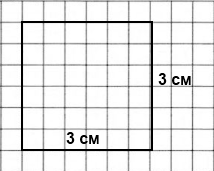
Завдання 6 Накресли квадрат, периметр якого дорівнює периметру прямокутника зі сторонами 2 см і 4 см
Нагадаємо.
Формула периметра прямокутника
Р = (а + b) • 2, де a – довжина прямокутника, b – ширина прямокутника
Формула периметра квадрата (всі сторони рівні)
Р = а • 4, де a – довжина сторони квадрата
(2 + 4) • 2 = 12 (см) – периметр прямокутника
12 : 4 = 3 (см) – сторона квадрата
Завдання 7 У цистерні було 480 відер води. Один насос може викачати всю воду за 24 хв, а інший — за 40 хв. За скільки хвилин можна викачати всю воду, якщо ввімкнути два насоси?
Розв'язання
1) 480 : 24 = 20 (в.) – викачає відер води перший насос за 1 хв.
2) 480 : 40 = 12 (в.) – викачає відер води другий насос за 1 хв.
3) 20 + 12 = 32 (в.) – викачають відер води два насоси разом за 1 хв.
4) 480 : 32 = 15 (хв) – потрібно хвилин.
Відповідь: два насоси викачають усю воду за 15 хвилин.
КОМБІНОВАНА КОНТРОЛЬНА РОБОТА № 8 Варіант 2
Завдання 1 Серед чисел (97 508, 750 860, 875 084, 75 083) число, у якому 7508 десятків і розклади на розрядні доданки
75 083
Міркуємо так
75 083 = 7508 дес. 3 од.
75 083 = 70 000 + 5 000 + 80 + 3
Завдання 2 1/8 від числа 120 336
|
120336 : 8 = 15042 Відповідь: 15042 |
_120336 | 8 8 15042 _ 40 40 _33 32 _16 0 |
Завдання 3 Рівняння
x - 700 = 25 • 20
х - 700 = 500
х = 500 + 700
х = 1200
Завдання 4 Значення виразу, якщо а = 44
6868 : (2437 - а • 55) + 334 = 738
Якщо а = 44, тоді 6868 : (2437 – а • 55) + 334 = 6868 : (2437 – 44 • 55) + 334 = 738
|
х 44 55 220 220 2420 |
_ 2437 2420 17 |
_6868 | 17 68 404 _68 68 0 |
+ 404 334 738 |
Завдання 5
420 с = 7 хв
2 год 12 хв = 132 хв
2 доби 18 год = 66 год
Міркуємо так
420 с = (420 : 60) хв = 7 хв
2 год 12 хв = 2 • 1 год + 12 хв = 2 • 60 хв + 12 хв = 120 хв + 12 хв = 132 хв
2 доби 18 год = 2 • 1 доба + 18 год = 2 • 24 год + 18 год = 48 год + 18 год = 66 год
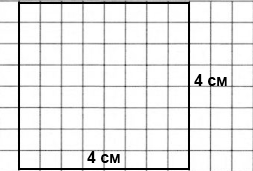
Завдання 6 Накресли квадрат, периметр якого дорівнює периметру прямокутника зі сторонами 5 см і 3 см.
Нагадаємо
Формула периметра прямокутника
Р = (а + b) • 2, де a – довжина прямокутника, b – ширина прямокутника
Формула периметра квадрата (всі сторони рівні)
Р = а • 4, де a – довжина сторони квадрата
(5 + 3) • 2 = 16 (см) – периметр прямокутника
16 : 4 = 4 (см) – сторона квадрата
Завдання 7 Перший автомобіль може перевезти 300 брикетів за 6 рейсів, а другий — за 3 рейси. За скільки рейсів можуть перевезти всі брикети два автомобілі, якщо працюватимуть разом?
Розв'язання
1) 300 : 6 = 50 (бр.) – перевезе брикетів за 1 рейс перший автомобіль.
2) 300 : 3 = 100 (бр.) – перевезе брикетів за 1 рейс другий автомобіль.
3) 50 + 100 = 150 (бр.) – перевезуть брикетів за 1 рейс два автомобілі разом.
4) 300 : 150 = 2 (р.) – потрібно рейсів, щоб перевезти всі брикети.
Відповідь: за 2 рейси можуть перевезти всі брикети два автомобілі, якщо працюватимуть разом.