Повторення за рік завдання 26 – 71 частина 2 Математика 4 клас Листопад нова програма

Завдання 26

Маса качки в 4 рази більша, ніж маса сороки. Маса чотирьох качок така сама, як маса одного лелеки. У скільки разів маса лелеки більша, ніж маса сороки?

Розв'язання

Нехай х (кг) — маса сороки, тоді 4х (кг) — маса качки, 16х (кг) — маса лелеки.

16х : х = 16 (р.) – у стільки разів маса лелеки більша, ніж сороки.

Завдання 27 Скільки годин в:

1/6 доби — 24 год : 6 = 4 год

3/4 доби — 24 год : 4 • 3 = 6 год • 3 = 18 год

Завдання 28 Знайди:

1) десяту частину кожного числа: 810, 1000, 620, 2000;

810 : 10 = 81

1000 : 10 = 100

620 : 10 = 62

2000 : 10 = 200

2) соту частину кожного числа: 2800, 1000, 10400, 3600, 4300.

2800 : 100 = 28

1000 : 100 = 10

10400 : 100 = 104

3600 : 100 = 36

4300 : 100 = 43

Завдання 29 Розглянь однакові прямокутники, які поділено на частини.

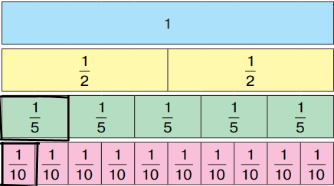
1) 1/5 прямокутника (одна частина зеленого кольору), 1/10 прямокутника (одна частина рожевого кольору).

2) Скільки десятих частин у 1/5 ? Дві. У 2/5? Чотири.

3) Користуючись малюнком, назви пропущені чисельники дробів, запиши ці рівності у зошит.

1/5 = 2/10; 6/10 = 3/5; 8/10 = 4/5; 4/5 = 8/10

Завдання 30

Купили 5 банок білої фарби і 7 банок зеленої за однаковою ціною. За всю покупку заплатили 1344 грн. Скільки гривень окремо заплатили за білу фарбу й за зелену?

^Ціна

^{Кількість банок}

^{Загальна вартість}

^{Біла фарба}

Однакова

^{5 шт.}

^{1344 грн}

^{Зелена фарба}

7 шт.

Розв'язання

1) 5 + 7 = 12 (шт.) – усього банок

2) 1344 : 12 = 112 (грн) – ціна банки

3) 112 • 5 = 560 (грн) – заплатили за білу фарбу

4) 112 • 7 = 784 (грн) – заплатили за зелену фарбу

Відповідь: заплатили 560 грн за білу фарбу і 784 грн за зелену фарбу.

Завдання 31

Зібрали 2 т 400 кг винограду. Скільки літрів соку отримають з нього, якщо з кожних 100 кг винограду виробляють 50 л соку?

^{Короткий запис}

^{50 л — 100 кг}

^{? — 2 т 400 кг}

Розв'язання

2 т 400 кг = 2400 кг

1 спосіб

1) 100 : 50 = 2 (кг) – потрібно винограду для отримання 1 л соку

2) 2400 : 2 = 1200 (л)

2 спосіб

1) 2400 : 100 = 24 (р.) – у стільки разів більше винограду

2) 50 • 24 = 1200 (л)

Відповідь: отримають 1200 л соку.

Завдання 32

З поля зібрали 1800 кг соняшникового насіння. Скільки літрів олії отримають із цього насіння, якщо з кожних 300 кг насіння отримують 100 л олії?

^{Короткий запис}

^{100 л — 300 кг}

^{? — 1800 кг}

Розв'язання

1 спосіб

1) 300 : 100 = 3 (кг) – потрібно насіння для отримання 1 л олії

2) 1800 : 3 = 600 (л)

2 спосіб

1) 1800 : 300 = 6 (р.) – у стільки разів більше насіння

2) 100 • 6 = 600 (л)

Відповідь: отримають 600 літрів олії.

Завдання 33

Сергій купив 3 конструктори, а Микита — 4. За всі конструктори вони заплатили 756 грн. Скільки грошей заплатив Сергій, а скільки — Микита, якщо ціна у всіх конструкторів однакова?

^Ціна

^{Кількість конструкторів}

^{Загальна вартість}

^Сергій

Однакова

^{3 шт.}

^{756 грн}

^Микита

4 шт.

Розв'язання

1) 3 + 4 = 7 (шт.) – всього конструкторів

2) 756 : 7 = (700 + 56) : 7 = 100 + 8 = 108 (грн) – ціна конструктора

3) 108 • 3 = 324 (грн) – заплатив Сергійко

4) 108 • 4 = 432 (грн) – заплатив Микита

Відповідь: Сергійко заплатив 324 гривні, Микита — 432 гривні.

Завдання 34

Першого дня в магазині продали 14 шкільних рюкзаків, а другого — 17 таких самих рюкзаків. Першого дня за рюкзаки одержали на 480 грн менше, ніж другого. Скільки гривень одержали за рюкзаки кожного дня окремо?

	^Ціна	^{Кількість рюкзаків}	^{Загальна вартість}
^I	Однакова	^{14 шт.}	^{?, на 480 грн менше}
^II	Однакова	17 шт.	^?

Розв'язання

1) 17 – 14 = 3 (шт.) – на стільки менше рюкзаків продали першого дня, ніж другого

2) 480 : 3 = (300 + 180) : 3 = 100 + 60 = 160 (грн) – ціна рюкзака

3) 160 • 14 = 2240 (грн) – одержали першого дня

4) 160 • 17 = 2720 (грн) – одержали другого дня

Відповідь: першого дня одержали 2240 гривень, другого дня — 2720 гривень.

Завдання 35

На хлібозаводі дві однакові бригади за 3 зміни випікають 12 т хліба. Скільки тонн хліба випече одна бригада за 2 зміни?

^{Короткий запис}

^{2 бр., 3 зм. — 12 т}

^{1 бр., 2 зм. — ?}

Розв'язання

1 спосіб

1) 12 : 3 = 4 (т) – випікають 2 бригади за 1 зміну

2) 4 : 2 = 2 (т) – випікає 1 бригада за 1 зміну

3) 2 • 2 = 4 (т) – випікає 1 бригада за 2 зміни

2 спосіб

1) 12 : 2 = 6 (т) – випікає 1 бригада за 3 зміни

2) 6 : 3 = 2 (т) – випікає 1 бригада за 1 зміну

3) 2 • 2 = 4 (т) – випікає 1 бригада за 2 зміни

Відповідь: за дві зміни бригада випече 4 т хліба.

Завдання 36

Два однакові коти за 30 днів з'їдають 6 кг сухого корму. Яку масу корму потрібно одному котові на 1 день?

^{Короткий запис}

^{2 к., 30 дн. — 6 кг}

^{1 к., 1 дн. — ?}

Розв'язання

6 кг = 6000 г

1 спосіб

1) 6000 : 30 = 200 (г) – з'їдають 2 коти за 1 день

2) 200 : 2 = 100 (г) – з'їдає 1 кіт за 1 день

2 спосіб

1) 6000 : 2 = 3000 (г) – з'їдає 1 кіт за 30 днів

2) 3000 : 30 = 100 (г) – з'їдає 1 кіт за 1 день

Відповідь: котові на день потрібно 100 г сухого корму.

Завдання 37

Дві однакові бригади будівельників за 8 год виготовляють 4 дерев'яні будиночки. За скільки годин одна бригада будівельників виготовить 2 такі будиночки?

^{Короткий запис}

^{2 бр., 8 год — 4 б.}

^{1 бр., ? год. — 2 б.}

Розв'язання

4 : 2 = 2 (б.) – будиночків виготовить одна бригада за 8 год

Відповідь: за 8 год одна така бригада будівельників виготовить два такі будиночки.

Пояснення: якщо дві бригади за 8 год виготовлять 4 будиночки, то одна бригада за ці 8 год виготовить удвічі менше, тобто 2 будиночки.

Завдання 38

Тузик з'їдає пакет сухого корму масою 6 кг за 30 днів, а Бім — за 20 днів. На скільки днів цього корму вистачить Тузикові й Біму?

^{Короткий запис}

^{Тузик — 30 дн. — 6 кг}

^{Бім — 20 дн. — 6 кг}

^{Разом — ? дн. — 6 кг}

Розв'язання

6 кг = 6000 г

1) 6000 : 30 = 200 (г) – з'їдає Тузик за 1 день

2) 6000 : 20 = 300 (г) – з'їдає Бім за 1 день

3) 200 + 300 = 500 (г) – з'їдають разом за 1 день

4) 6000 : 500 = 12 (дн.)

Відповідь: сухого корму вистачить на 12 днів.

Завдання 39

Брати Зіновій і Матвій хочуть виготовити з паперу 60 корабликів. Старший Зіновій може виготовити ці кораблики за 3 год, а молодший Матвій — за 6 год. За скільки годин вони зможуть виготовити ці кораблики, якщо працюватимуть разом?

^{Короткий запис}

^{Зіновій — 3 год — 60 к.}

^{Матвій — 6 год — 60 к.}

^{Разом — ? год — 60 к.}

Розв'язання

1) 60 : 3 = 20 (к.) – виготовляє Зіновій за 1 год

2) 60 : 6 = 10 (к.) – виготовляє Матвій за 1 год

3) 20 + 10 = 30 (к.) – виготовлять разом за 1 год

4) 60 : 30 = 2 (год)

Відповідь: за 2 год брати виготовлять ці кораблики.

Завдання 40

На обід бабуся вирішила приготувати 60 вареників. Вона може зліпити цю кількість вареників за 30 хв, а її внучка — за 60 хв. За скільки хвилин вони зліплять 60 вареників, якщо працюватимуть разом?

^{Короткий запис}

^{Бабуся — 30 хв — 60 в.}

^{Внучка — 60 хв — 60 в.}

^{Разом — ? хв — 60 в.}

Розв'язання

1) 60 : 30 = 2 (в.) – робить бабуся за 1 хв

2) 60 : 60 = 1 (в.) – робить внучка за 1 хв

3) 2 + 1 = 3 (в.) – роблять разом за 1 хв

4) 60 : 3 = 20 (хв)

Відповідь: 60 вареників бабуся з внучкою зліплять за 20 хв.

Завдання 41

Ворона пролетіла 200 м зі швидкістю 8 м/с. Скільки часу вона витратила на політ?

^{Короткий запис}

^{Відстань — 200 м}

^{Швидкість — 8 м/с}

^{Час — ?}

Розв'язання

200 : 8 = 25 (с)

Відповідь: ворона витратила на політ 25 секунд.

Завдання 42

Швидкісний потяг за 5 год проходить відстань завдовжки 450 км. З якою швидкістю рухається потяг?

^{Короткий запис}

^{Відстань — 450 км}

^{Час — 5 год}

^{Швидкість — ?}

Розв'язання

450 : 5 = 90 (км/год)

Відповідь: потяг рухається зі швидкістю 90 км/год.

Завдання 43

Учень виконав вимірювання, але не записав одиниць вимірювання. Назви їх.

Площа класної кімнати — 24 м². Площа поверхні стола — 77 дм². Площа поверхні зошита — 340 см².

Завдання 44

Для подарунка мамі Максим виготовив кухонну дошку, що має форму прямокутника зі сторонами 18 см і 25 см. Знайди площу цієї дошки.

^{Короткий запис}

^{Ширина — 18 см}

^{Довжина — 25 см}

^{Площа — ?}

Розв'язання

х 18

450 (см²)

Відповідь: площа дошки 450 см².

Завдання 45

Знайди площу кожної геометричної фігури за умови, що сторона кожної клітинки дорівнює 1 см.

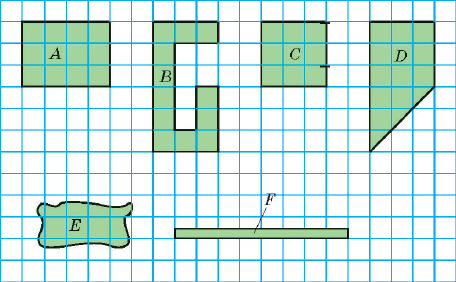
Розв'язання

1 спосіб

S = 1 см • 1 см = 1 см² – площа одної клітинки

S = 1 см² • 12 = 12 см² – площа фігури А.

S = 1 см² • 12 = 12 см² – площа фігури В.

S = 1 см² • 9 = 9 см² – площа фігури С.

S = 100 мм² • 12 + (100 мм² + 100 мм² + 100 мм²) : 2 = 1200 мм² + 300 мм² : 2 =

= 1200 мм² + 150 мм² = 1350 мм² – площа фігури D

S = 1 см² • 3 + 1 см² • 12 : 2 = 9 см² – площа фігури Е

S = 1 см² • 8 : 2 = 4 см² – площа фігури F

2 спосіб

1) 4 • 3 = 12 (см²) – площа фігури А

2) 6 • 3 – 2 • 2 – 1 • 2 = 18 – 4 – 2 = 12 (см²) – площа фігури B

3) 3 • 3 = 9 (см²) – площа фігури С

4) 30 • 30 + 30 • 30 : 2 = 1350 (мм²) – площа фігури D

5) 3 + 12 : 2 = 3 + 6 = 9 (см²) – площа фігури Е

6) 8 • 1 : 2 = 4 (см²) – площа фігури F

Завдання 46

У фермерському господарстві заклали сад, що має форму прямокутника. Сума довжини й ширини саду дорівнює 1500 м, причому ширина у 2 рази менша, ніж його довжина. Сад обнесено огорожею. Визнач:

1) площу саду в гектарах;

1) 1500 : 3 = 500 (м) – ширина саду

2) 1500 – 500 = 1000 (м) – довжина саду

3) 1000 • 500 = 500000 (м²) = 50 (га) – площа саду

2) довжину всієї огорожі.

1) 1500 : 3 = 500 (м) – ширина саду

2) 1500 – 500 = 1000 (м) – довжина саду

3) (1000 + 500) • 2 = 3000 (м) – довжина огорожі саду

Завдання 47

Загорожа для овечок прилягає до стіни кошари, що має довжину 15 м. Довжина всієї загорожі становить 99 м. Знайди площу ділянки, відведеної для овечок.

Розв'язання

1) 99 – 15 = 84 (м) – дві рівні довжини

2) 84 : 2 = 42 (м) – одна довжина

3) 42 • 15 = 630 (м²)

Відповідь: площа ділянки 630 м².

х 42

210

630

Завдання 48

Для виготовлення паперових іграшок взяли аркуш червоного паперу площею 600 см² і аркуш блакитного, площа якого на 80 см² більша. Довжина червоного аркуша — 30 см. Знайди довжину блакитного аркуша, якщо відомо, що ширина обох аркушів однакова.

	Ширина	Довжина	Площа
Червоний аркуш	Однакова	30 см	600 см²
Блакитний аркуш	Однакова	17 шт.	?, на 80 см² більша

Розв'язання

1) 600 + 80 = 680 (см²) – площа блакитного аркуша

2) 600 : 30 = 20 (см) – ширина червоного аркуша

3) 680 : 20 = 34 (см)

Відповідь: довжина блакитного аркуша 34 см.

Завдання 49

Площа дослідного поля становить 86000 м². Частину цього поля, що має форму прямокутника зі сторонами 240 м і 160 м, засіяно просом, а решту площі — гречкою. Яку площу засіяно гречкою?

Короткий запис

Загальна площа — 86000 м²

Площа проса — ?, 240 м і 160 м

Площа гречки — ?, решта

Розв'язання

1) 240 • 160 = 38400 (м²) – площа, засіяна просом

2) 86000 – 38400 = 47600 (м²)

Відповідь: гречкою засіяно 47600 м².

х 240

160

144

38400

_86000

38400

47600

Завдання 50

Довжина кухні дорівнює 4 м, а її ширина — 3 м 20 см. Скільки потрібно квадратних плиток зі стороною 4 дм, щоб викласти ними підлогу?

^{Короткий запис}

^{Площа кухні — ?, 4 м х 3 м 20 см}

^{Площа плитки — ?, 4 дм х 4 дм}

^{У скільки разів більше — ?}

Розв'язання

4 м = 400 см, 3 м 20 см = 320 см

1) 400 • 320 = 128000 (см²) = 1280 (дм²) – площа кухні

2) 4 • 4 = 16 (дм²) – площа плитки

3) 1280 : 16 = 80 (пл.)

Відповідь: потрібно 80 плиток.

Завдання 51

Розглянь прямокутник ABCD. Відрізок BD, що сполучає протилежні вершини цього прямокутника, називають діагоналлю. Накресли в зошиті такий самий прямокутник і проведи в ньому діагоналі.

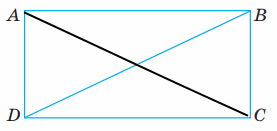
Завдання 52

Проведіть дослідження. Виріжте з паперу різні прямокутники. Проведіть у кожному діагональ. Розріжте прямокутник по діагоналі. Накладіть утворені частини одна на одну. Зробіть висновок про рівність трикутників. Трикутники рівні.

Завдання 53

Побудуй квадрат зі стороною 5 см. Проведи в ньому діагоналі.

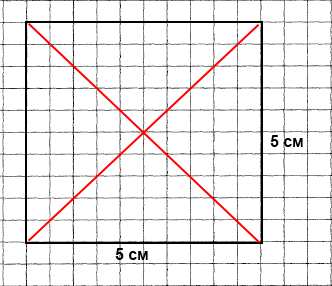
Виміряй їх довжину і зроби висновок. Діагоналі рівні.

Завдання 54

Діагоналі прямокутника ABCD перетинаються в точці О. Виміряй діагоналі. Виміряй відрізки AO, BO, DO, CO. Зроби висновок.

АО = ВО = DO = CO

Діагоналі рівні.

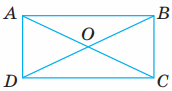
Завдання 55

Накресли квадрат зі стороною 6 см. Проведи в ньому діагоналі.

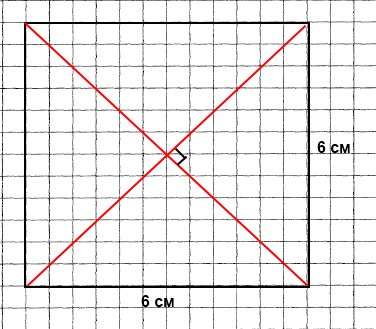
Які кути утворилися при їх перетині? Прямі

Завдання 56

Визнач площу зафарбованого трикутника.

Розв'язання

1) 6 • 2 = 12 (см²) – площа прямокутника

2) 12 : 2 = 6 (см²)

Відповідь: площа зафарбованого трикутника 6 см².

Завдання 57

Назви елементів куба: вершина, ребро, грань

Куб має 8 вершин, 6 граней і 12 ребер. Усі грані куба рівні квадрати. Усі ребра куба також рівні. Грані куба утворюють поверхню куба.

Завдання 58

Довжина ребра куба дорівнює 5 см. Обчисли площу поверхні куба.

Розв'язання

1) 5 • 5 = 25 (см²) – площа одної грані

2) 25 • 6 = 150 (см²)

Відповідь: площа поверхні куба 150 см².

Завдання 59

Укажи, на якому малюнку зображено розгортку куба. На другому малюнку

Завдання 60

Назви елементів прямокутного паралелепіпеда: вершина, ребро, грань.

Паралелепіпед має 8 вершин, 6 граней і 12 ребер. Усі грані паралелепіпеда — прямокутники.

Завдання 61

Розглянь світлини. Назви об'єкти, які мають форму прямокутного паралелепіпеда. Шафа, коробка, будинок

Завдання 62

Радіус кола із центром у точці С дорівнює 3 см, а радіус кола із центром у точці Р дорівнює 4 см. Яка відстань між точками А і В?

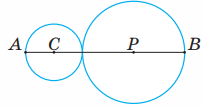
Розв'язання

3 + 3 + 4 + 4 = 14 (см) – довжина відрізка АВ

Завдання 63

Трикутник, що має прямий кут, називають прямокутним.

Трикутник, що має тупий кут, називають тупокутним.

Якщо в трикутнику всі кути гострі, то його називають гострокутним.

Завдання 64

Назви номери прямокутних трикутників: 4, 6, 8

Номери гострокутних трикутників: 1, 5, 7

Номери тупокутних трикутників: 2, 3, 9

Завдання 65 Одиниці вимірювання місткості.

Місткість – це об'єм. Один мілілітр становить 1/1000 літри.

Завдання 66

Прочитай, яку місткість має кожна посудина в мілілітрах:

250 мл – двісті п'ятдесят мл

110 мл – сто десять мл

500 мл – п'ятсот мл

Завдання 67

Чайник містить 1800 мл води. Чи вистачить цієї води на 8 чашок місткістю 250 мл?

^{Короткий запис}

^{Вода — 1800 мл}

^{1 чашка — 250 мл}

^{8 чашок — ?}

^{Чи вистачить — ?}

Розв'язання

250 • 8 = 2000 (мл) – об'єм 8 чашок місткістю 250 мл

1800 < 2000

Відповідь: не вистачить.

Завдання 68

Малий пластиковий стакан містить х мл води, а великий — у мл. Скільки всього мілілітрів води буде міститися в чотирьох великих і трьох малих стаканах?

	^{Місткість склянки}	^{Кількість склянок}	^{Загальна місткість}
^Малі	^{х мл}	³	^?	?
^Великі	^{у мл}	4	^?	?